基于闸口资源配置的送箱集卡预约优化模型*
于 蒙 周 密
(武汉理工大学物流工程学院 武汉 430063)
0 引 言
随着国际贸易的快速发展,集装箱进出口量越来越大,集卡作为运输集装箱的主要工具,其需求量也快速增加,这将出现高峰时期港口运输集装箱的集卡同时抵达码头,造成港口各个节点拥堵.由于码头是一个集成作业系统,一个环节的作业效率将影响整个码头的作业效率,所以,港口拥堵将降低整个码头的作业效率.
为缓解集卡在港口的拥堵,国内外很多港口,如洛杉矶港、温哥华港,以及上海洋山港等先后实行了集卡预约系统.国内外学者也做了很多研究,Chen等[1]通过为每支到港船舶制定时间窗来管理集卡的到达,从而缓解集装箱码头闸口的拥堵.Zhang等[2]利用休假式排队模型描述场桥协同服务内外集卡的过程,基于非平稳的排队理论更准确的估计了外集卡在闸口和堆场的平均等待时间.Yi等[3]提出了一种预约调度方法,该方法考虑了停留在码头内的集卡成本、滞期费、集装箱运输成本,每个时间窗和每个区块允许的约会次数以及每个时间窗内可用集卡的数量.与以前的研究不同,该研究在构建预约时间表时考虑预约对终端等待时间的影响.利用基于Frank-Wolfe算法的数学公式和启发式算法,以在合理的计算时间内解决该问题;滕藤等[4]为缓解码头的拥堵问题,利用基于支持向量机和卡尔曼滤波的方法预测集卡到达的时间,提高集卡到达时间的准确性;曾庆成等[5]在预约模型中考虑了内部集卡对堆场作业的影响,提出了基于内外集卡协同服务的优化模型,利用休假式排队系统,结合遗传算法优化集卡在码头的等待成本;杨惠云等[6]根据不同预约时段集卡到达类型的不同来改变闸口的数量,结果表明,可变闸口调度的集卡预约优化减少了集卡的排队时间.
综上所述,目前码头集卡预约排队模型大多考虑集卡到达、服务分布等规律,而未考虑码头资源的优化配置.闸口通道数和堆场的容量有限也是造成码头拥堵的原因,以送箱集卡为研究对象,当闸口通道数目有限时,可根据不同预约时段集卡的集港数量来安排闸口数[7-8].因此,在考虑码头现有设施条件下,优化其闸口的资源配置,建立集卡到港预约排队模型,并结合自适应遗传算法优化集卡预约额,从而使集卡在闸口和堆场的平均等待时间最小.
1 集卡预约优化模型的构建
1.1 问题描述
集卡进入码头后,先后经过闸口和堆场完成运输任务,然后从出场闸口离开.在码头实际中,港口集装箱的进出口业务繁多,集卡到港时间的随机性是码头拥堵的重要原因,集卡预约可控制集卡的集港量,使集卡到港时间相对确定.闸口通道数有限也会造成集卡大量排队,闸口送提箱通道的业务不同,所需的服务时间也不同,当送箱通道服务有过大压力时,在不影响提箱集卡作业的前提下,可开放一定数量的提箱通道协助送箱集卡完成进闸业务.集卡进入堆场后,需要在堆场排队,若堆场排队队长过长,堆场容量有限,反过来又会导致集卡在闸口的排队[9].
为解决上述问题,在集卡预约模式下,考虑闸口资源和堆场容量对集卡排队的影响建立预约模型.在闸口处,可视为M/M/C(t)的排队模型,每个堆场分区满足M/G/1/R的排队模型,以集卡在闸口和堆场平均等待时间最小为优化目标,优化各时段的预约份额,建立如下模型.
1.2 预约模型的建立
1.2.1参数定义
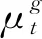
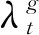
1.2.2预约模型的构建
目标函数:
(1)
约束条件:
(2)
(3)
m=T/p
(4)
闸口处:
(5)
(6)
(7)
(8)
(9)
(10)
(11)
堆场处:
(12)
(13)
(14)
(15)
(16)
(17)
(18)
式(1)为集卡在闸口和堆场平均等待时间最小;式(2)为集卡总数等于决策期内预约份额之和;式(3)为在预约时段内集卡未到和迟到后实际到达的数量;式(4)为将预约时段p划分为t的数量;式(5)为t时刻集卡到达闸口的量;式(6)为t时刻在闸口g的集卡到达量;式(7)为t时刻第g个闸口利用率与队长的关系;式(8)为在闸口g处集卡排队和不需要排队的队长;式(9)为t时刻第g个闸口集卡的离开量;式(10)为集卡P时段在闸口的平均等待时间;式(11)为闸口处集卡在决策期的平均等待时间;式(12)为t时刻集卡到达堆场的量;式(13)为t时刻堆场队长与利用率的关系;式(14)为堆场y处集卡排队和不需要排队的队长;式(15)为集卡在任意时刻不超过其容量限制;式(16)为t时刻集卡离开堆场的量;式(17)为集卡P时段在堆场的平均等待时间;式(18)为堆场处集卡在决策期的平均等待时间.
2 算法设计
由于传统遗传算法在进化过程中最优解易丢失,容易陷入局部最优解,所以,本文采用适应度值排序的自适应遗传算法,使算法不易陷入局部最优,具体算法步骤如下.
步骤1编码及种群初始化 染色体采用实数编码的方式进行编码,一条染色体的长度为决策期内预约时段数,其基因值表示集卡预约数,首先随机生成一组正整数,使其和等于在决策期内集卡的预约总数,图1为一条染色体,初始种群数为200.

图1 染色体示意图
步骤2
碧洲计算适应度 根据模型约束式(2)~式(18),计算每个个体的排队等待时间
F
,其适应度值
f
可见式(19),计算每条染色体的适应度值,并求出种群适应度的平均值与个体适应度值排序.
f=1/F
(19)
步骤3选择与交叉 本文采用轮盘赌进行选择,随机从父代中选择两个个体交叉,由于本文采用的实数编码,所以采用融合交叉的方式对父代染色体进行交叉,见式(20),其中α为参数,0<α<1.
(20)
将选中的两个个体适应度值较大的排序号代入到计算交叉概率pc的式(21)中,用适应度值的排序号替代适应度值能适当增加迭代后期的交叉概率,从而使算法不易陷入局部最优.
式中:N1为选中的两个染色体中适应度值较大的序号;N2为种群平均适应度值的序号;N3为种群最大适应度值的序号;Pc1为最大交叉概率;Pc2为最小交叉概率.
步骤4变异 变异采用实值变异的方式,为确保变异后解的可行性且便以操作,随机选中染色体的两点,保证两点的差值为(0,3],互换两点的数值即可实现变异操作,变异过程见图2.
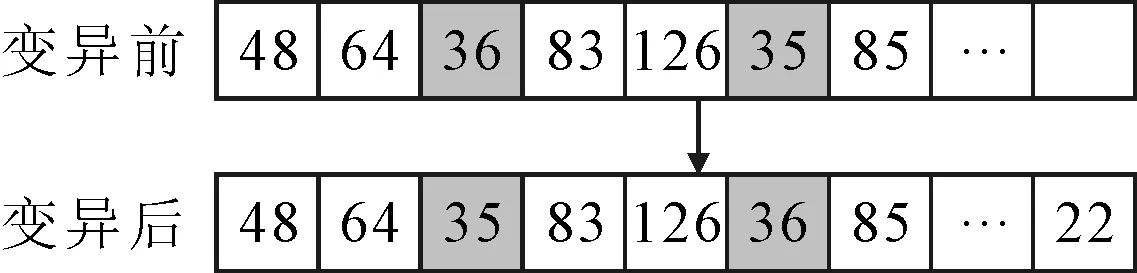
图2 染色体变异示意图
变异概率pm按式(22)进行自适应调整,其中,Pm1为最大变异概率,Pm2为最小变异概率.
(22)
步骤5算法终止 当进化次数达到最大进化次数后,算法终止,得出集卡预约等待时间最小的预约方案作为最优解,否则算法返回第二步.
3 实例分析
3.1 算例设计
以某集装箱码头为例进行分析,将决策期N定为7 d,并将其分为84个预约时段,所以每个预约时段长度为2 h.该码头有八个进场闸口,每个闸口的服务能力为40辆/h,场桥服务能力为20辆/h,决策期内集卡预约到港量为5 000辆 ,堆场最大容量为10.
该码头闸口有四个送箱通道,四个提箱通道,在不影响提箱集卡作业的前提条件下,本文只考虑送箱集卡的预约优化问题.当预约两小时内集卡的到港数小于40辆时,满足闸口和堆场的服务能力,此时开放1个送箱通道;当预约两小时内集卡的到港数在161~200辆时,此时需要开放4个送箱通道和1个提箱通道.由于每个预约时段的集卡到达量在变化,所以各预约时段集卡所需的闸口通道数见表1,这样不仅可提高闸口的利用率,也能节约码头资源.

表1 不同时段集卡预约到港量对应的闸口通道数目
3.2 模型验证
通过以上数据,运用matlab对预约模型进行编程,见图3,得出集卡在码头的平均等待时间为14.13 min,根据对码头的调研,集卡的实际平均周转时间大约为22 min,验证了建立模型的可行性.
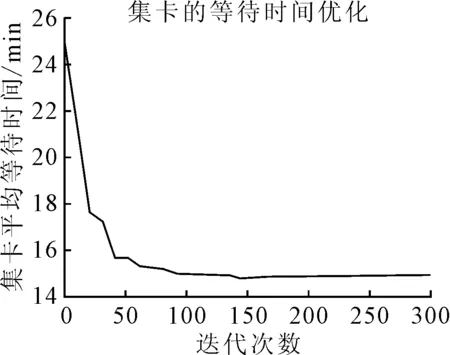
图3 算法收敛图
3.3 预约优化模型验证
图4为有无预约情况下等待时间和集卡到达量的对比,发现未实施预约前,集卡在某些时段大量集港,存在拥堵现象,而某些时段集港数极低,造成码头资源的浪费;实施预约后,集卡在每个预约时段的集港数量控制在50~80辆,将高峰时段的集卡数分散到集港低谷期,有效的减少了码头拥堵现象.
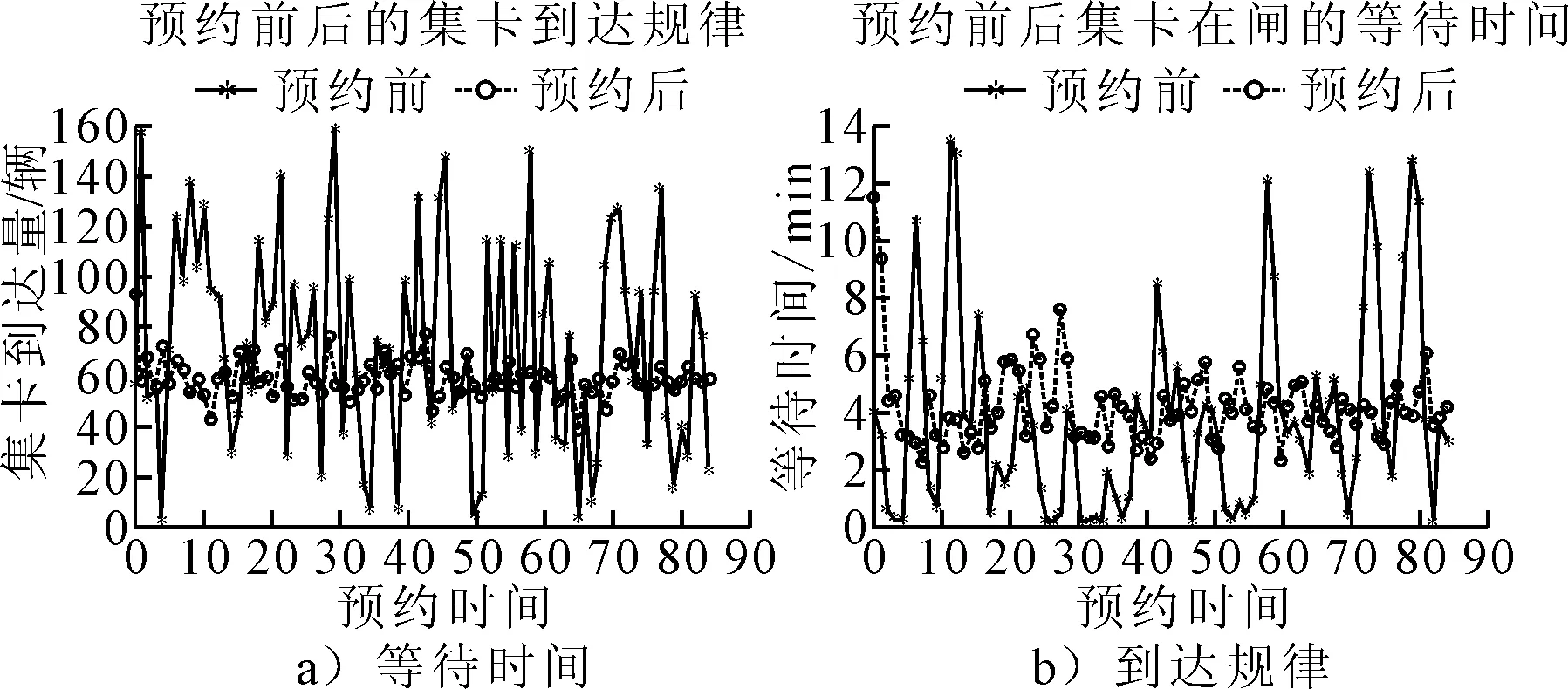
图4 集卡到港规律对比
预约实施前后集卡在码头的平均等待时间变化见表2,变化趋势见图5.结果表明,未实施预约前,在闸口处集卡的平均等待时间为4.89 min,最高等待时间为13.86 min,预约后平均等待时间降为3.97 min,减少约1 min,相比未预约之前,集卡集港较均匀,所以预约集港能明显降低集卡的排队时间.

表2 集卡在码头的等待时间 min
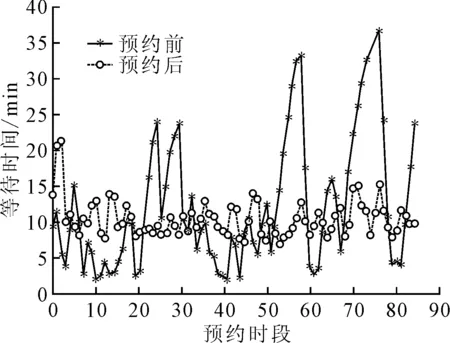
图5 集卡在码头的排队等待时间
未实施预约前,在堆场处集卡的平均等待时间为15.73 min,最高等待时间约为38 min,预约后集卡的平均等待时间降为10.16 min,减少了5.57 min,预约后最高等待时间降为20 min.
4 结 束 语
为解决集卡在集装箱码头的堵塞问题,在闸口处,通过设置可变闸口的方式来配置闸口通道资源,在堆场处,考虑场桥的服务能力来限制堆场容量,从而提高整个码头的通行能力.本文考虑闸口和堆场的条件约束构建了集卡预约优化模型,通过优化各时段的集卡预约到港数目来减少集卡的平均等待时间.为求解预约优化模型,设计了采用适应度值排序的自适应的遗传算法来求解模型.结果表明,考虑闸口和堆场资源限制的预约模型能有效的减少集卡在闸口和堆场的排队时间.

