空轨曲线梁角变形及横向加劲肋合理间距分析

陶 奇，李 周，郑晓龙，游励晖

(1.中国中铁二院工程集团有限责任公司，四川成都 610031；2.中建钢构有限公司，广东深圳 518000)

空轨在德国、日本等国家应用较多，在国内属于新兴的轨道交通，目前尚无一条运营线路建成，相关的技术标准和设计规范有待建立或完善。文献[1-3]对空轨交通系统及其在国内的适应性进行了系统论述。文献[4-7]阐述了空轨系统轨道梁及桥墩的构造特点和设计原则，对空轨系统轨道梁及桥墩进行了试探性设计。文献[8-10]对空轨车辆系统进行了论述。

轨道梁作为空轨系统的重要组成部分和设计技术要点，其结构具有独特性。其轨道梁一般采用开口钢箱截面，车辆转向架置于梁内，“梁-轨合一”，即轨道梁底板同时又是轨道，这与其他轨道交通的梁结构形式存在巨大差异。

该系统为全线高架结构，线路适应性极强，其曲直梁比例一般大于50 %，最小曲线半径可达30m，最大简支曲线梁跨度可达25m。在轨道梁的制造、运输、架设施工时，钢箱轨道梁均会产生各种变形，尤其是曲线轨道梁，进而影响到走行轨(钢箱梁底板)、导向轨及稳定轨(钢箱梁腹板)的平顺性。强大的横向加劲肋是减小结构变形的有效措施之一，对轨道梁 “套箍作用”，限制其变形。目前，世界范围内仅德国和日本有空轨运营线，日本空轨车辆轴重较大，一般在5.5t以上，最大可达9t，其横向加劲肋往往采用的是刚度极大的箱型结构(加劲箱)，间距1.4～2.0m。德国空轨车辆轴重一般小于4t，其横向加劲肋一般采用30mm厚150mm高的的钢板，间距1.6m。国内空轨基本上是全套引进的德国技术，在其基础上做了一些改进，轴重一般介于德国和日本之间，约4.0～5.5t，隔板尺寸与德国无异，但间距有所变化，介于1.0～1.6m之间。其中，中车青岛四方试验线(轴重5.0t)和成都中唐试验线(轴重4.0t)横向加劲肋间距均为1.6m，国内第一条空轨运营线(在建)大邑空轨其直线段横向加劲肋间距1.2m，曲线段横向加劲肋间距1.0m。

为了较精确地模拟轨道梁的变形，合理确定钢箱横向加劲肋的设置间距，现以空轨曲线标准25m跨径轨道梁为例，分析其在设置不同间距的横向加劲肋和列车荷载作用时钢箱轨道梁的角变形，探讨影响变形的因素，提出横向加劲肋合理间距的建议，并归纳总结出相关结论。

1 变形分析

1.1 计算荷载

空轨轨道梁为一种下部开口的薄壁矩形截面钢箱梁，车体悬挂于轨道梁下方，转向架置于梁体内腔，包含走行轮，导向轮及稳定轮，车辆荷载主要通过走行轮作用于轨道梁底板，横向摇摆力、车体风荷载和离心力等通过稳定轮和导向轮传至轨道梁腹板，梁体受力较正常钢箱梁复杂，轨道梁腹板多向受力，车轮作用处断面荷载作用如图1所示。

在图1所示荷载作用下，钢箱梁顶板受面外弯矩及压力作用，底板受两个方向面外弯矩、剪力、拉力和局部压力(轮压)作用，腹板受面内、外弯矩，剪力，拉力和压力共同作用，与常规钢箱梁相比，顶底板受力差异较小，只是承压面由顶板换到底板，但是腹板受力有明显差异，腹板承受一个非常大的面外弯矩，因此，腹板设计与常规钢箱梁会有差别较大，与此同时，加劲肋设置也会有明显差异，除需抵抗截面畸变变形外，还需抵抗腹板弯曲变形。

计算分析时，仅考虑结构自重、二期恒载及车辆荷载。其中钢材容重按78.5kN/m3计，二期恒载考虑供电轨、回流轨、供电电缆及电缆槽等设备荷载，合计按4.73kN/m计算。车辆荷载2节车编组，荷载图示如图2所示。关于活载冲击系数，暂按2019年河南省颁布的的空轨地方设计标准[11]采用，按1+μ=1+20/(45+L)考虑，式中L为桥梁跨度。

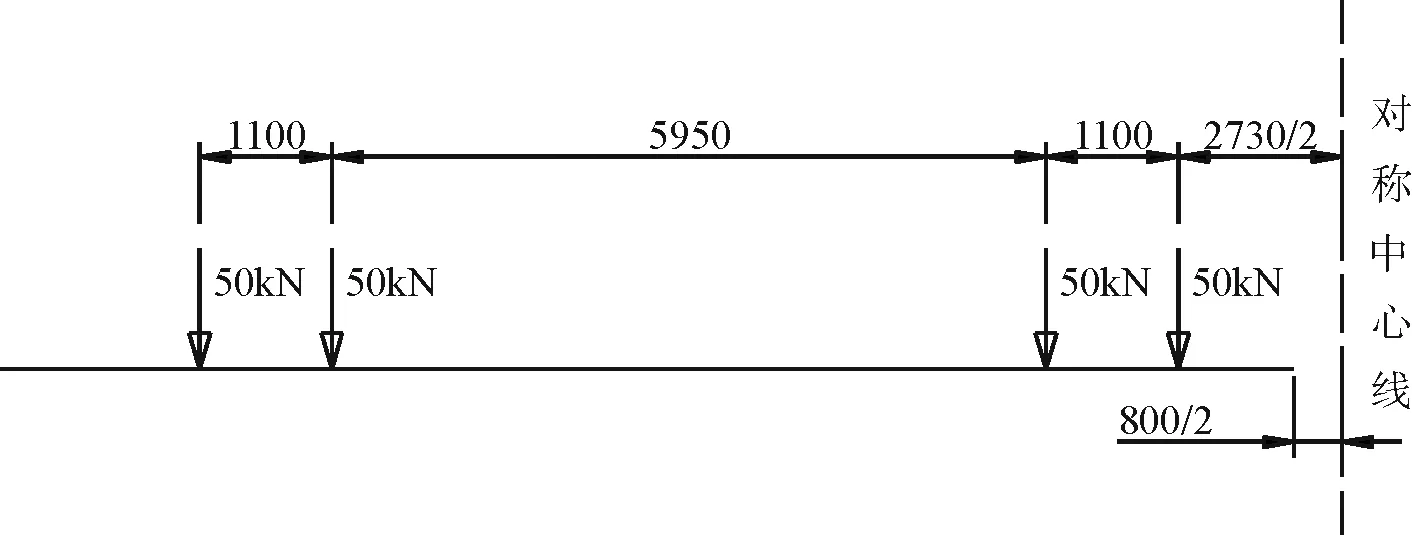
图2 车辆荷载(单位：mm)

计算时，车辆荷载每个轴均按均布荷载施加于板单元之上，车辆走行轮直径518mm，横向宽度110mm，考虑走行轮1mm的竖向变形量(走行轮为实心橡胶轮胎，竖向变形量由车辆厂家提供)，则车轮与轨道梁底板的接触面尺寸为110mm×43mm。模拟时，为保证跨中截面产生最大角变形，将车辆荷载的中轴作用于轨道梁中部(非对称布置，活载图示偏离跨中截面2730/2=1365mm进行加载)。

1.2 荷载组合

计算时主要考虑两种荷载组合，如表1所示，其中计算活载时考虑了冲击系数。

表1 荷载组合

1.3 变形分析

位于曲线上的钢箱梁，在荷载作用下(包括自重)，相对于各截面的形心会产生一个轴向扭矩，从而引起截面的扭转变形。对于开口截面，其扭转变形可分为自由扭转、约束扭转和畸变变形。自由扭转是无纵向约束的刚性转动，截面上各点纤维在纵向均可以自由伸缩，构件的每一个截面受扭之后都不再是平面，而是出现凹凸不平的曲面，从而产生翘曲变形，这时截面不会出现正应力，而只产生自由扭转剪应力。如果受扭时截面纵向纤维不能自由伸缩，使得截面不能翘曲，则称此为约束扭转。截面会产生翘曲正应力，当两个相邻截面的翘曲正应力不相同时，还会产生翘曲剪应力。自由扭转和约束扭转都是假定箱梁在扭转时截面周边保持不变形，为刚体转动。当截面较薄或横隔板较少时，截面不仅发生转动，还要发生畸变。

畸变变形(即受扭时截面周边的变形)的主要变形特征是畸变角。在畸变作用下箱型构件的矩形截面变形后不再保持原来的形状。畸变变形的存在使截面上产生了正应力以及剪应力。同时，畸变变形还会使截面各板件上产生横向挠曲变形，因此还会在截面上产生横向正应力。大量的工程实践表明，薄壁钢箱梁结构畸变效应不可忽略[12-14]，在实际工程中，一般采用在箱形截面内设置横隔板或者加劲环来达到减轻畸变效应影响的目的。

空轨交通系统与一般轨道交通系统差别较大，主要表现在：(1)车辆系统转向架置于轨道梁内侧；(2)轨道梁采用开口薄壁钢箱梁结构，扭转刚度较小；(3)车辆荷载(活载)较大，一般约为轨道梁自重的两倍。以上3点因素造成轨道梁在荷载作用下易产生畸变变形。又因车辆系统转向架置于轨道梁内侧，使得结构的变形需要严格控制，尤其是畸变变形，否则车辆行驶过程中可能会出现转向架卡顿或者车轮与轨道脱空现象，影响行车舒适性，甚至可能影响车体转向架和轨道梁结构安全。同时，因荷载直接作用于开口轨道梁底板的顶面，横隔板除了限制结构畸变变形外，还需要抵抗轨道梁顶板、底板及腹板的面外弯曲变形，因此，横隔板的作用更为重要，但由于空轨轨道梁的工作空间位于箱梁内部空间，所以无法设置内横隔板，实际工程中，通过在箱梁外侧设置横向环形加劲肋来对箱梁畸变进行限制以及抵抗腹板弯曲变形。

本文假定轨道梁截面变形如图3所示，顶板宽度为B，底板宽度B1, 腹板高度为H，如整个截面仅发生刚体扭转变形，则顶板、腹板和底板扭转角应相等或者相近，否则说明截面发生了畸变变形或者弯曲变形，定义α1、α2、α3、α4为箱型截面四个角对应的角变形(包含畸变变形及弯曲变形)，则有：

(1)

(2)

(3)

(4)

因为顶板、底板及腹板肯定存在一定的弯曲变形，腹板变形后程曲线状态，按上述4式计算所得结果不精确，实际计算时，取各角点相邻两个单元来进行计算即可消腹板变形对计算结果带来的影响(图3)。

图3 截面变形示意(虚线为变形后，A、E为曲线内侧)

1.4 控制指标

2 模型建立

以25m跨空轨标准曲线轨道梁为例，桥梁所在的平曲线半径R=200m(车辆不限速最小曲线半径，由车辆生产厂家提供，一般正线设计时此曲线半径应用极多)，箱梁截面高度H=1.25m(内净高)，宽度B=0.78m(内净宽)，两块底板下侧分别设置一道纵向加劲，加劲肋厚24mm，高80mm，底板厚30mm，顶板厚28mm，腹板厚24mm，其断面如图4所示。构件材料为Q345qD钢材，材料弹性模量E=2.1×1011MPa，泊松比μ=0.3，密度ρ=7850kg/m3。

图4 25m跨曲线轨道梁标准断面(单位：mm)

计算时横向加劲肋均采用30mm厚，150mm高钢板(目前国内几条试验线和正在施工的运营线均采用此规格，其强度、刚度及稳定性已经通过试验线验证)，工况考虑5种，间距分别对应1.0m、1.2m、1.4m、1.6m、1.8m及2.0m，每种工况横向加劲肋均未包含各梁端1.5m范围内设置的4道横向加劲肋。

采用通用有限元分析软件SNSYS建模，各钢板均采用SHELL63板单元模拟，建模时考虑了梁端牛腿，25道横向加劲肋轨道梁空间有限元模型如图5所示，模型共包含39 393个单元。

图5 有限元模型

3 恒载作用下计算截面的角变形

空轨轨道梁在吊装架设阶段及铺设二期恒载阶段，结构主要受恒载作用，建模分析跨中截面及梁端截面的角变形。分别按图3所示，提取各角点位移值，按式(1)～式(4)分别计算α1、α2、α3、α4值，计算结果如图6～图7所示。

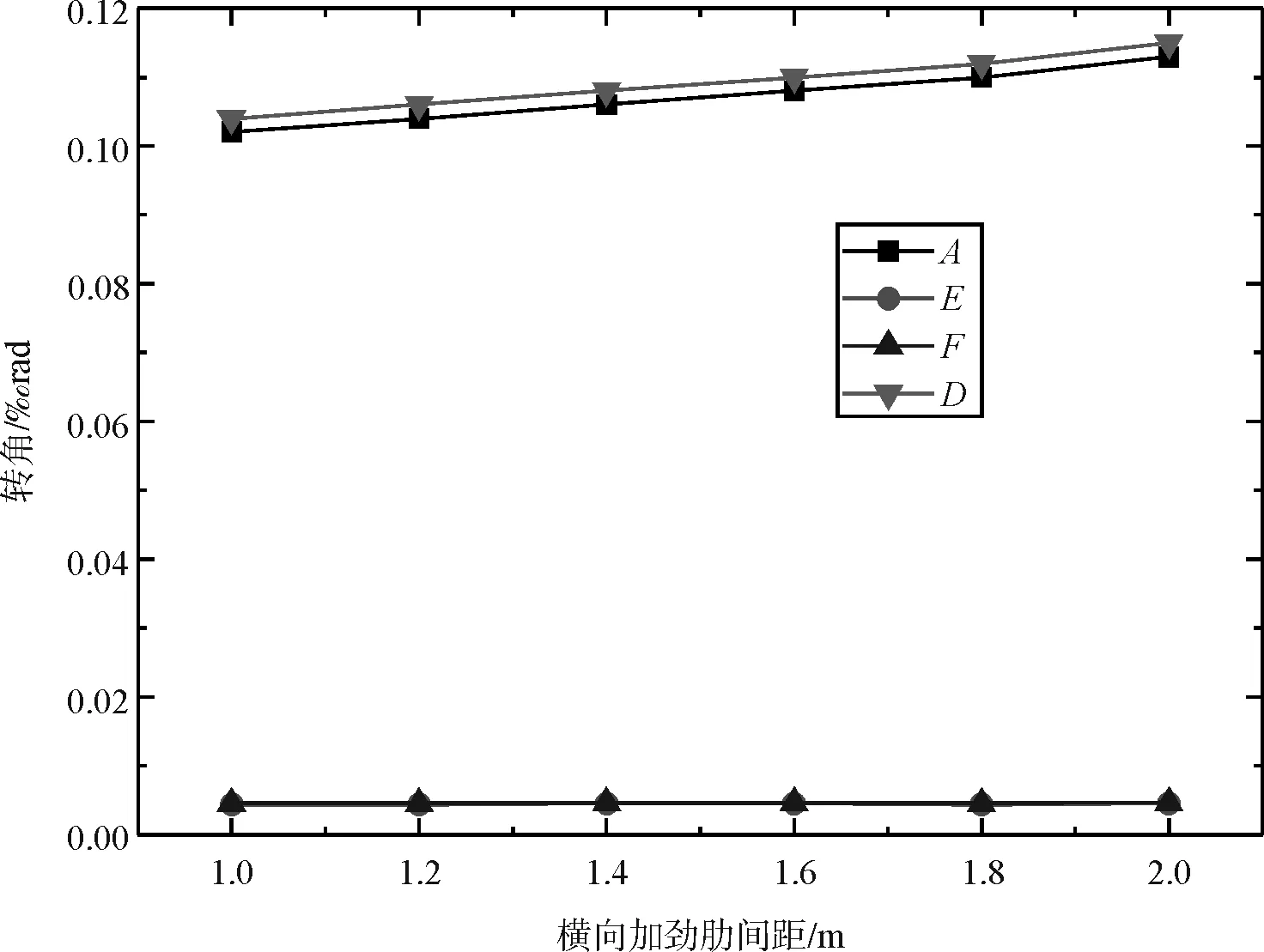
图6 恒载作用下梁端截面各点角变形

图7 恒载作用下跨中截面各点角变形

从图6可以看出，在恒载作用下，横向加劲肋间距不同时，梁端截面各角点的角变形最大值约0.12 ‰rad，远小于限值7 ‰rad，说明梁端横向加劲肋具有足够的刚度。从底板角变形曲线的变化趋势看，随着横隔板数量增加，梁端截面角变形均有减小趋势，表明横向加劲肋对截面角变形有抑制作用。同时，对比4条曲线，可以明显看出，底板角变形明显大于顶板角变形，约为其25倍，其原因可能是顶板所受约束较开口的底板更强所致，且顶板位置除具有4道横向加劲肋外，其还与刚度极大的支座牛腿固结，变形完全被限制所致，其值几乎完全不受隔板数量影响。

从图7可以看出，在恒载作用下，跨中截面角变形呈现与梁端角变形较为相似的规律，但又有不同，主要体现在：(1)角变形最大值约为0.37 ‰rad，比梁端最大角变形大约3倍，但也满足限值要求；(2)顶板对应的角变形值增加幅度较大，其原因应该是跨中截面顶板约束小于梁端截面；(3)顶、底板均表现出随横向加劲肋数量增加角变形有减小趋势。

从图6、图7中还可以看出，截面外侧角点F、D处角变形均比内侧角点A、E角变形略大，表明开口曲梁在受恒载作用时，外侧荷载高于内侧荷载。

4 主力作用下计算截面的角变形

主力作用按前述荷载工况定义为恒载与活载的共同作用。对于活载，取最不利的跨中位置进行计算分析(此时因梁体的弯曲而产生的等效扭矩最大)，确保此时轨道梁各截面的的最大角变形满足限值要求即可确定整个轨道梁在移动活载的作用下最大角变形亦满足限值要求，从而判断横向加劲肋设置是否满足要求。

计算截面仍取跨中截面和梁端截面，分别按图3所示，提取各角点位移值，按式(1)～式(4)分别计算α1、α2、α3、α4值，计算结果如图8、图9所示。

图8 主力作用下梁端截面各点角变形

图9 主力作用下跨中截面各点角变形

从图8可以看出，在主力作用下，横向加劲肋间距不同时，梁端截面各角点的最大角变形约为0.85 ‰rad，远大于恒载作用下的变形值，但也满足限值要求，说明梁端横向加劲肋具有足够的刚度。从底板角变形曲线的变化趋势看，随着横隔板数量增加，角变形均有减小的趋势，这与恒载作用下的规律相同。对比顶、底板变形值可以看出底板角变形远大于顶板角变形，约为其130倍，说明梁端支座顶板支座位置的刚度极大，在任何外荷载作用下，几乎不发生畸变变形。

从图9可以看出，在主力作用下，横向加劲肋间距不同时，跨中截面底板对应两角点的角变形大于底板两角点对应角变形角变形，约为其2.3～3.8倍，且随着隔板间距增加急剧增大，在横向加劲肋间距1.8m时，其值已达到7.8 ‰rad，约为间距1.0m时对应角变形值的3倍，已超限值7 ‰rad，在间距2.0m时，其值已达到9.7 ‰rad，远超限值，不满足要求。

与恒载作用下效果类似的是，在主力作用下截面外侧角点F、D处角变形也均比内侧角点A、E角变形略大，表明开口曲梁在受主力作用时，外侧荷载也高于内侧荷载，说明曲梁在受均布或者集中荷载作用时，均有外侧梁所受荷载高于内侧梁现象，因此，在做设计时可结合加工难度，适当考虑内外侧横向加劲肋不对称设计。

主力对跨中截面各角点产生的角变形远大于恒载产生的角变形，原因应该是活载较大(约为梁体重量的2倍)，且施加活载时，轮载作用点位置正好处于跨中截面，使得此处产生最大变形，实际设计时，也应该如此考虑，保证结构各截面最大角变形满足限值要求。

综合以上计算分析结果可以看出，横向加劲肋间距不易超过1.6m，超过1.6m后角变形超限，可能影响行车舒适性及结构安全，同时，横向加劲肋间距也不易小于1.2m，小于1.2m可能会造成一定程度的浪费，横向加劲肋间距不同时其工程量如表2所示，从表2中可以看出，横向加劲肋间距为1m时较1.2m时每米钢材用量增加0.04t，双线(实际工程一般均为双线)即增加0.08t，则每公里增加钢材80t，按正常价格1.5万元/t(Q345qD、E级钢综合单价，随钢材价格波动，此值为国内多座空轨项目可研阶段计算所得结果)计算，即每公里增加约120万元，空轨项目为全线高架桥梁结构，一般线路长度10km以上，因此，可为单个项目节约1千万元以上。如果对比1.6m间距横向加劲肋，则整个项目因为此项设计即可节约2 000万元以上。空轨为一种新生的交通制式，造价的提升不易于制式的推广应用，因此，设计时尽量做到精确设计，保证结构满足使用要求的同时尽量减少工程造价。

表2 横向加劲肋不同间距对应的工程量

5 结论

利用ANSYS有限元分析软件，模拟空轨25m标准曲线轨道梁在不同间距横向加劲肋及不同外荷载作用下梁端及跨中截面的角变形，得到以下结论：

(1)梁端因支座需要，设置了强大的横向加劲肋，使得跨内横向加劲肋间距的变化对梁端截面角变形影响不大，在恒载及主力作用下，其角变形值均远小于限值。

(2)恒载作用下，横向加劲肋间距从1.0～2.0m变化时，跨中截面各角变形均能满足限值要求，但在主力作用下，横向加劲肋间距超过1.8m时跨中截面底板位置角变形已不满足限值要求，且随着间距的进一步增加，顶、底板角变形值均有加速增大的趋势。

(3)横向加劲肋间距的设置应结合不同的车辆荷载，利用本文所述方法计算出角变形值，再综合考虑工程数量进行最终确定。建议：车辆轴重3.5～4.5t时，曲线梁横向加劲肋间距取1.3～1.4m；车辆轴重4.5～5.5t时，曲线梁横向加劲肋间距取1.2～1.3m。