立足真问题 追寻度量的本真
钱敏芳

摘 要针对《角的度量》来说,该节课的主要目标是为了促使学生掌握角的概念,在全面了解角是有大小之分的基础上加深对相关知识点的印象,以便可以为学生日后学习角的分类奠定扎实的基础。
关键词角的度量;教学设计;教学能力
中图分类号:G622 文献标识码:A 文章编号:1002-7661(2020)17-0164-01
随着新课程改革的颁布与实施,对小学数学教学提出了更高的要求,尤其在课程设计方面,更是需要教师积极转变教学理论,调整教学模式,帮助学生更好地理解与记忆知识点。
一、直面问题
《角的度量》是人教版四年级上册的内容,新课学完过后,笔者请了部分四年级的同学参与测评。
请用量角器测量以下几个角的度数。
图(1)学生能很快测量出角的度数60°,而且读数准确。
图(2)有个别同学摆放时,稍有犹豫,而且读数时有读错圈或反着读刻度的情况。原角75°,有同学读数时读成105°或85°。
图(3)、图(4)问题比较大,不少同学摆来摆去,要失误多次后才能找到正确的摆放方式。个别能力弱的同学甚至无从下手。读数时,也频频出错,分不清哪个圈。
二、分析思考
角的度量是測量中难度最大的,平时教学中,老师们会反复强调测量方法:三重合(即角的顶点与量角器的中心点重合,角的一条边与0刻度线重合,角的另一条边与几刻度线重合就是几度),并让学生反复模仿练习。
三、调整策略
(一)复习旧知,引发矛盾冲突,铺垫新知
1.师:同学们,上节课我们认识了角,你知道怎样画一个角吗?(从一点引出两条射线,所形成的图形就是角)
2.比较∠1和∠2的大小。
小结:角的两条边张开得大,角就大一些;角的两条边张开得小,角就小一些(直观判断)
3.出示∠3,让学生比较∠1和∠3的大小。
生:移动∠1至∠3的位置,让∠1和∠3的顶点重合,一条边重合,看另一条边。(图2所示)
师:那∠1比∠3大多少呢?
(通过∠1、∠3比较,揭示量角必要性。)
(二)认识量角器和角的计量单位
1.引出计量角的单位
师:刚才我们计量长度时用了一个1厘米的长度单位,计量面积时用了一个1平方厘米的面积单位,那么计量角度呢?(需要一个1度的角作单位)
明确:可以用1度角作为计量单位。(1度角,记作:1°)
师:只要我们知道∠1、∠2中有多少个1°角,就知道∠1和∠2的大小了。但这个1°角实在是太小了,操作起来不方便,能不能想个办法呢?(把很多的1°角拼起来)
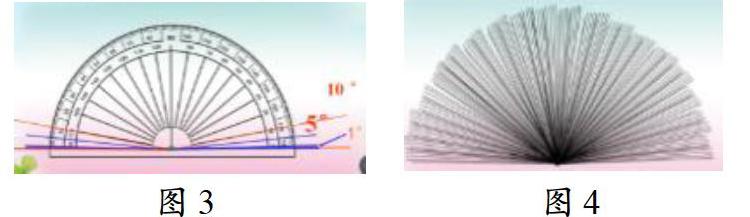
师:这么密密麻麻的,多乱啊,数起来也不方便啊?(可以把它简化一下,标上刻度,如图3)
师:仔细观察量角器,你看到了些什么?同桌之间相互说说。
2.组织全班交流,明确:(课件配合演示)
(1)量角器是一个半圆形,把半圆平均分成180等份,每一份就是几度角?(1°)量角器可以看作是由180个1°角拼在一起的。
(2)这180个1°角的共同顶点就是量角器的中心点。
(3)因为这180个1°角可以从左边数起,也可以从右边数起,从左边数起的0刻度线和从右边数起的0刻度线统称为:零刻度线。0刻度线的0刻度在外圈的就看外圈刻度,0刻度在内圈的就看内圈刻度。所以量角器有两圈刻度,即内圈刻度和外圈刻度。
参考文献:
[1]潘红娟.又一次被颠覆——俞正强老师“角的度量”一课赏析[J].中国教师,2015(10).

