基于离散元方法与水动力学耦合的河冰动力学模型

翟必垚，刘 璐，张宝森，沈洪道，季顺迎

（1.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024；2.黄河水利委员会 黄河水利科学研究院，河南 郑州 450003；3.美国Clarkson大学 土木与环境工程系，波兹坦 纽约 13699-5710）

1 研究背景

河冰在我国高寒地区的河流中非常常见，如黄河宁蒙及山东河段、黑龙江上游、松花江依兰以下河段、嫩江上游等［1］。河冰的动力过程非常复杂，其包含流体力学、固体力学，以及流体和固体的相互作用，其中流凌和冰坝是比较常见并备受关注的河冰现象［2-4］。流凌不仅会影响航运，其巨大的动能还会撞击破坏桥墩和其他水工构筑物。冰坝的形成会减小河道的正常过流断面，加之封冻冰层对水的摩擦阻力，必然阻隔上游来水导致槽蓄水量增加，不断抬高上游水位，可在极短时间内形成凌汛险情，造成严重的自然灾害［5-6］。

现场观测、物模试验和数值计算一直是河冰研究的三个主要手段，而随着研究认识的深入和计算机的发展，数值模拟越来越得到人们的重视。国外对冰塞冰坝的研究最早开始于Pariset 和Hausse（1961）对冰盖前缘水动力条件和冰盖稳定时平衡状态的受力分析，并由此建立了判断冰盖是否向上游发展的弗劳德数条件以及稳定冰塞的平衡方程［7］。后来其他研究者在其基础上建立一维静态冰塞冰坝模型［8-10］，包括RIVJAM、HEC-RAS等［11］。Beltaos和Burrell对冰坝的形成、演变和溃决过程中的水位和冰厚进行了大量的观测和分析，并与模型结合得到了很好的模拟结果［12-13］。这些模型能够计算冰塞冰坝的形状和水位状态，其不足之处是无法计算冰塞形成的动力过程、冰水相互影响的过程，因此也无法预测冰塞发生的概率、位置和时间［14-15］。之后，一维和二维河冰动力学模型相继发展起来。并可以描述河冰的输移和初始冰塞的形成［16］，如DynaRICE［14，17］、SPIKI［18］等。同时，国内对河冰的研究也取得了很大进展，从河冰力学性质研究［19-20］到数学模型研究［21-25］都做了大量的工作，并结合我国河流的具体情况，在工程应用中取得了理想的研究成果［26-28］。

然而，对于以上提到的河冰数值模型，大部分都是将河冰作为连续体而忽略了冰块挤压破碎的动力过程。离散元法则可以很好地表征冰块运动时的接触过程和黏结破碎过程，近年来在海冰领域被广泛采用［29-31］。在海冰离散元研究中，因为水动力不如河流中那样强烈，因此大多没有考虑海冰对水力条件的影响。在河冰领域中，离散元法的应用还较为少见。Hopkins 等［32-34］开展了前期初步研究，并发现离散元法在冰塞冰坝形成、冰块与桥墩、拦冰栅等结构相互作用等方面具有很强的优势。离散元法中最早采用球形颗粒和圆盘颗粒，近年来不同类型的非规则单元已相继发展起来［35-37］。扩展多面体单元作为一种新的离散单元构造方法，在一定程度上避免球形离散单元中细观计算参数的经验性［38］。针对冰盖武开河产生的碎冰以及由冰与河岸、冰与桥墩等水工结构物的相互作用而破碎形成的碎冰，扩展多面体单元可更加真实地反映碎冰的几何形态。

为此，本文将采用扩展多面体单元构造河冰离散元方法，采用有限元方法求解河冰影响下的水动力学，将河冰离散元方法与水动力学有限元方法相耦合以建立河冰的动力学模型。采用以上方法对明流冰封过程的水力条件变化过程进行数值模拟，验证本文计算模型的有效性，并对冰坝的形成过程进行数值模拟。

2 离散元方法与水动力学耦合的河冰动力学模型

本文建立的河冰动力学模型主要包括四个部分，即：河冰的动力学方程求解、扩展多面体单元求解冰块受到的接触力、二维水动力模型求解水力条件，以及耦合模型中冰水信息的传递和冰水相互影响的过程。

2.1 河冰动力学方程河冰输移主要受到风和水流的拖曳力、水面梯度力、冰块间的相互作用、河冰与河岸河床及水工建筑物的相互作用，如图1所示。由此，河冰运动的动力方程式为［14］：

式中：Mi为河冰单元的质量；vi为河冰单元的速度；t为时间；G为重力沿水面坡度的分量；Fa为风对冰块的拖曳力；Fw为水对冰块的作用力，包括水的拖曳力、浮力；Ri为河冰接触力，包括河冰冰块间、河冰与河岸河床及水工建筑物的接触力，其主要通过离散元方法求得。

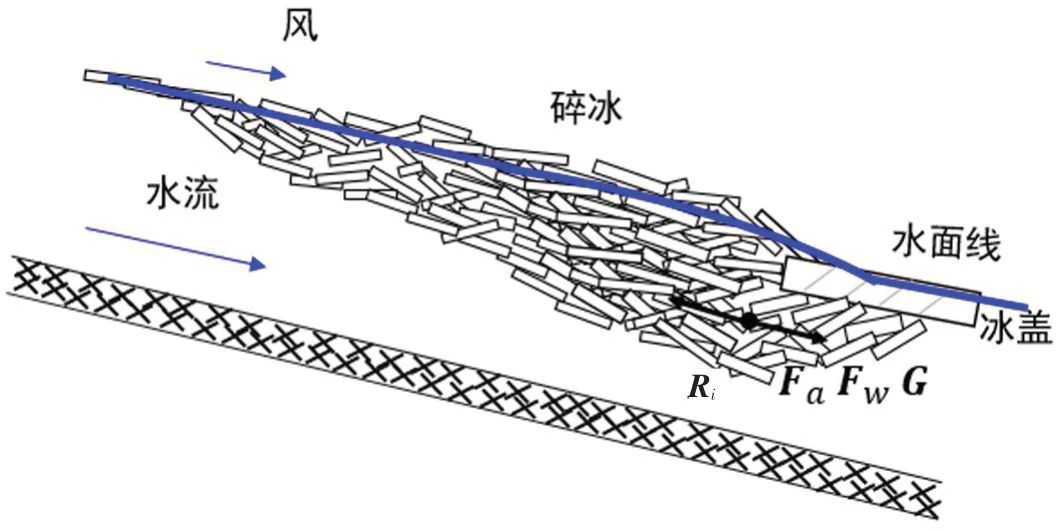
图1 河冰动力过程的受力分析

2.2 河冰扩展多面体离散元方法扩展多面体离散元方法是基于多面体离散元和球体离散元发展起来的，通过Minkowski Sum理论进行构造［39］，可写作：

图2 基于Minkowski Sum理论扩展多面体的构造

式中：A、B为两个单元的空间体；x、y分别为基础多面体A和扩展球体B内的坐标矢量［39-40］，即按照Minkowski Sum理论求和后，会得到具有光滑表面的扩展多面体，如图2所示。接触搜索判断也由角点与棱边的搜索判断转化为球面与柱面的搜索判断，由此有效提高计算效率。

在离散元求解过程中需要确定每个时间步接触单元间的接触点以及单元重叠量。单元的接触判断是基于包络函数的优化求解方法，引入二阶多面体扩展函数g，其定义的几何形态与扩展多面体具有很高的相似性，可写作：

式中：g（x、y、z）为多面体扩展函数；N为多面体的表面数量；ai、bi和ci分别表示多面体第i个面单位外法向的三个分量；di是第i个面到坐标原点的距离；r是函数的扩展半径；是Macaulay括号，且有即求点(x，y，z)到某个面的距离。

通过二阶多面体扩展函数与球面函数加权求和的函数形式可构造具有多面体特征的光滑颗粒，即：

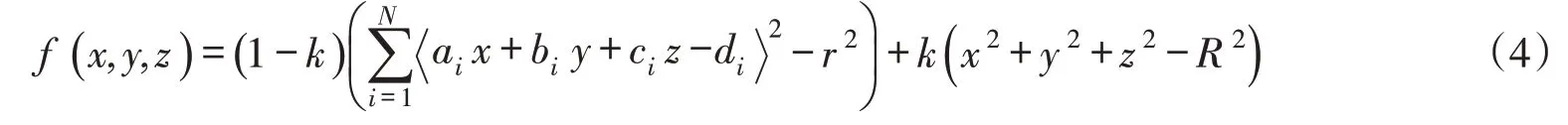
式中：f（x、y、z）为扩展多面体外表面函数；k为颗粒光滑度系数，0 ＜k≤1。当k越小时，单元越接近多面体形态；R为球面函数的半径。由该函数定义扩展多面体的包络函数并建立相应的优化方程：min(fA+fB)，s.t.fA-fB=0，fA和fB分别是两个颗粒的形态方程。通过光滑度系数k由大到小渐变的方法计算迭代初始点，并在基本多面体上进行迭代确定最终接触点和接触的重叠量δ=min‖XA-XB‖-(rA+rB)，XA和XB分别为扩展多面体内部基本多面体表面上的点，rA和rB是扩展半径［41］。

扩展多面体单元间的作用力采用非线性接触模型，可写作：

式中：Fn为法向力，由法向弹性力和法向阻尼力组成；Ft为切向力，由切向弹性力F te和切向阻尼力组成；kn为法向接触刚度，E *和R*分别是等效弹性模量和等效颗粒半径，νA、νB为颗粒的泊松比；EA、EB为颗粒的弹性模量；RA、RB为颗粒的半径；δn、δt分别是法向和切向重叠量；分别是法向和切向相对速度；cn、ct分别是法向和切向阻尼系数，其中mAB为等效质量mA、mB为颗粒质量；ζn为无量纲阻尼系数，可表示为e是颗粒回弹系数；δtmax为最大切向重叠量，表征最大静摩擦来限制切向接触力，即δtmax=μδn( 2-ν)( 2-2ν)，这里μ为颗粒间摩擦函数，ν为泊松比。

2.3 二维河流水动力模型河冰动力模型中的水动力学采用DynaRICE 模型中的水力方程与求解方法［14］。河流水动力学方程是基于动量守恒的二维浅水方程推导而来并考虑了表面冰的影响［14］。整个控制方程包括连续性方程和动量方程，其分别写作：

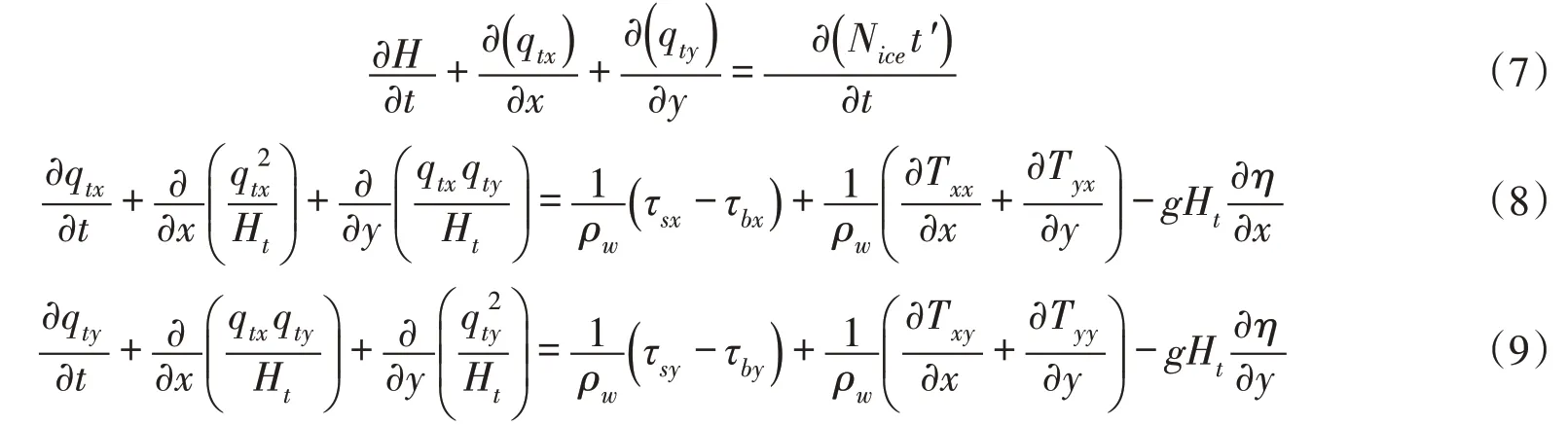
式中：x、y和t分别是空间和时间变量；H、Ht分别是总的水深和冰盖下的水深；η是水面高程；qtx、qty是总的流量沿x方向和y方向的分量；Nice是冰的密集度；t′是冰在水中的厚度；ρw为水的密度；τs、τb分别是冰对水流及河床对水流的摩擦力；τsx、τsy、τbx、τby分别是其沿x和y方向的分量；这里εxy是广义涡流黏性系数。

河水流量分为冰层流量和冰下流量两部分，即qt=qu+ql。冰层中的水流一方面会随着冰一起运动，一方面也会因为河流表面的水平坡度而发生渗流。

单位河宽上冰层部分的流量可以写成：

式中：qi为随冰块一起运动的河水流量；vi为冰量；qs=VsΔH为在冰层中运动的渗流流量；Vs=usi+vs j为渗滤流速，us和vs是其沿x和y方向的分量；冰层中的渗流是由河流的水力坡降产生；渗流流速Vs与水面坡降J的关系可以表示为［42］：

式中：λ为渗流系数，与冰的孔隙率、形状、冰块的大小等因素有关，一般取λ=1.0～1.6m/s。

2.4 扩展多面体离散元方法与水动力学的耦合模型河冰动力过程中的强水动力作用使得冰与水流间的相互作用不可忽略。本文建立的河冰动力学模型对水和冰的耦合处理通过以下几个方面进行：在水力模型方程中考虑表面冰对水流的影响，基于扩展多面体离散单元与三角形有限单元的相对位置通过插值平均进行信息交换，水对冰的作用通过对离散单元上的受力计算完成。

（1）水与冰间的计算参数交换。河冰的离散元计算是在拉格朗日坐标下进行的，水动力的有限元法计算则是基于欧拉坐标系。河冰的厚度、速度等信息与水动力学信息之间的传递是通过对离散单元与有限元网格节点相对位置进行插值计算得到。假设P为某一离散单元的质心，其所在的三角形网格的三节点分别为A、B、C，河冰计算所需要的流速、水深等水力信息由所在网格节点的信息加权求得，如图3所示，fP=∑Φi fi，其中Φi=Si Stotal（i=a，b，c），Si是第i个三角形的面积，Stotal是整个三角形单元的总面积，fP可以为流速、水面高度、水深等水力变量。

图3 冰与水间计算参数传递计算

然而，河流水力计算所需要的河冰信息则由该有限单元网格内的所有离散元颗粒信息的平均值求得，均值结果作为该有限单元网格内的值，即其中，下标E是该三角形单元编号，i表示三角单元中的离散单元编号，NP是三角单元中的离散颗粒数总和，f表示河冰离散元颗粒的速度、剖面厚度等参数。网格节点的值通过其所在所有单元网格的值进行平均求得，如图3中节点A的参数

（2）浮力、拖曳力及水面梯度力。水对冰的作用力主要有浮力、拖曳力以及水面梯度力，如图4所示。浮力大小与冰块浸没在水下的体积有关，通过多面体质心与多面体水下部分每个三角面组成的四面体体积Vi求和计算，即Vsub=∑Vi。冰块的总浮力Fb=Vsub ρw gk，k为竖直单位矢量；冰块受到的浮力矩为：Mb=rb×Fb，其中rb为由质心指向水下浮心的向量。浮心的确定可由公式计算，这里Oi是水下四面体的质心。

图4 河冰离散单元受浮力、拖曳力与水面梯度力计算

水流对冰块的拖曳力Fd和拖曳力矩Md可分别写作［31］：

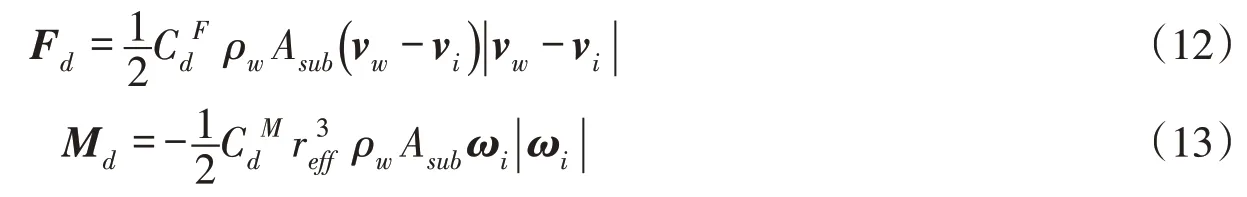
式中：、C dM是拖曳力和拖曳力矩系数；vw、vi分别为流速和冰速；Asub为冰块与水的接触面积在水流方向的投影；reff是冰块的有效半径，即块体所有顶点到质心距离的平均值；ωi是块体转速。

风对冰块的拖曳力与流对冰的拖曳力原理与计算方式相同，这里不再说明。通过这种方法对水流拖曳力和拖曳力矩进行计算，考虑了冰块与水的接触面在水流方向的投影面积对水流拖曳力的影响，拖曳力造成冰块的平移，拖曳力矩造成冰块的翻转。然而，由于水动力计算采用了二维的水力模型，忽略了流速沿水深方向的变化，因此公式中的流速实际上是此处沿水深方向的平均流速。并且计算中未考虑在竖直方向的流速对冰块的扰动，冰块竖直方向的运动只受到浮力和浮力矩的影响。在河冰输移过程中，竖直方向的流速相对于水流流动方向的速度较小，对河冰的影响也比较小，一定程度上可以忽略。但是在形成冰塞或冰盖后，冰盖前缘处的水流竖向扰动会促使前缘冰块的翻转下潜或者竖直下潜，对冰塞的形成有一定的影响，这会在之后的模型发展中考虑。

河冰的水面梯度力是由水面坡降造成的冰块重力沿水面下降坡度的分量，即G=Gx i+Gy j，其中，ηice是该河冰颗粒对应位置的水面高度，和是沿x方向和y方向的水面梯度。

（3）冰、水计算时间步耦合。数值计算中的时间步是影响计算稳定性、计算精度和计算效率的重要参数。离散元方法假定一个计算时间步内，颗粒受力和加速度保持恒定不变，这里采用了瑞利波法时间步进行计算［43］

式中：rmin为计算颗粒中最小扩展半径；ρi为河冰离散元颗粒的密度；剪切模量E为弹性模量。在实际计算中，要依据颗粒运动的剧烈程度选取合适的时间步长以保证计算的稳定性，这里取进行计算。

在水动力学有限元计算中，临界时间步长为：

式中：ΔL为计算域中三角形网格的最小边长；Hmax为最大水深。在实际计算中，根据流场水力变化的剧烈情况会稍微调整步长，一般取

水与冰间的计算参数交换频率由耦合时间步决定，耦合时间步根据实际冰水作用的剧烈程度进行人为设置，一般取10～60 s。对于冰水动力过程较为剧烈的情况采用小的耦合时间步，对于冰水动力过程相对缓和的情况采用大耦合时间步。每当模拟时间为耦合时间步的整数倍时，即可交换水冰间的计算参数。具体过程如图5所示。

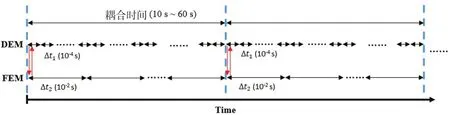
图5 计算耦合时间步

3 矩形河道内封河水位变化的数值模拟

将以上河冰动力学模型应用到规则河道进行简单工况的数值模拟，并通过与DynaRICE的计算结果和理论分析结果对比来检验模型的有效性与准确性。DynaRICE 模型由美国Clarkson大学沈洪道教授建立，已在多条河流动力学模拟中得到验证［14，17］并在国际上被广泛认可。

开阔水域在冬季经常遇到封河的现象，河流上方的冰盖会改变河道的综合糙率及水力半径，从而使河流的水力条件发生很大变化。先分析开阔水域产生冰盖后水力条件的变化，然后再对该过程进行数值模拟。

图6 明渠与暗渠水力参数示意

曼宁公式可反映水流与河床的部分关系以及河床内部各因素之间的相互关系。这里假设封河情况下，冰盖不向下游运动，则通过曼宁公式可求得规则河道内的均匀流水深，其基本表达式为：

式中：Q为水文断面的流量，m3/s；Ac为过水断面的面积，m2；n为糙率；Rh为水力半径，m；Sf为水力坡降。冰盖的出现改变了明渠流的水力条件，如图6所示，其在曼宁公式的使用上有一定的区别。

在规则矩形河道明渠均匀流中，糙率等于河底糙率，即n=nb；水力半径Rh=，这里Ac=Bcdw；湿周Pc=Pb=2dw+Bc，Bc和dw分别是河宽和水深。式（16）整理后为h为水深，这里等于dw。

在河道有冰盖的条件下，湿周增加了上层冰盖部分，即Pc=Pb+Pi=( 2dw+Bc)+Bc=2(dw+Bc)，糙率等于河底糙率nb与冰盖底部糙率ni的综合糙率。综合糙率的计算公式形式多样，被广泛应用的有Belokon-Sabaneev 公式、Einstein 公式和Larsen 公式［44］。由于在模拟中采用的是宽深比较小的矩形明渠，因此这里采用误差较小的Einstein公式计算综合糙率，即：

式中α为床面区和冰盖区的湿周比，此处由此整理后得到最终水深需考虑冰盖中的部分，即这里hi为冰厚。通过曼宁公式计算的正常水深，将作为模拟结果准确性检验的参照。当表面冰存在向下游流动的速度时，以上分析则需要重新考虑冰速的影响［17］。

这里规则矩形河道的长度L=2000 m，宽度Bc=10 m，如图7（a）所示。河底坡降Sf=0.4×10-3，河床糙率nb=0.035，冰盖糙率ni=0.02，上游边界设定恒定流量Q=3.17m3/s，下游边界设定正常水深h=0.59 m，主要计算参数列于表1。图8为均匀恒定明渠流初始时刻的纵向水力参数。在明渠流的稳定状态下，沿河道方向各处流速基本稳定在0.55 m/s，水深稳定在0.59 m。

在稳定明渠流的水面上生成0.2 m厚的冰盖，冰块单元分布如图7（b）所示，上下游的边界条件恒定不变，计算初始的水位流速保持与明渠流一致。随着冰盖的出现，附加的冰边界增加了水流流动的阻力并导致过流能力减小。采用本文模型计算了2个小时的河冰动力学过程，结果如图9所示。这里给出2 min、10 min、1 h和2 h时的冰水状态。

表1 规则矩形河道明渠与封河的模拟参数

图7 明渠流与有冰暗渠流模拟

图8 明渠流的初始水力参数

在保持上游流量以及下游水位边界条件恒定的情况下，当河道存在冰盖时，水位先由上游开始壅高并逐渐往下游抬高，最终在下游水位边界条件的影响范围以外基本都达到了正常水深。采用Dy⁃naRICE对这一过程进行了数值模拟，计算结果与本文方法的对比情况如图10所示。图10（a）和图10（b）分别是流速和水深的对比。在初始阶段2 min时，流速和水深较DynaRICE 的结果都有一些偏差；在10 min时，偏差显著缩小；在之后的1～2 h时，两个模型的结果几乎完全吻合。这在一定程度上验证了本文计算模型的有效性。

以上计算中的前期偏差主要是离散元模型中水面的壅高过程稍稍滞后于DynaRICE。这是由于离散元的冰块颗粒在水中是三维的运动形式，在初期水位快速抬升的过程中冰块会有不稳定的上下浮动，冰下厚度随之不断变化，而冰对水流的糙率与冰的水下厚度有关。这就使得水流受到的冰下摩擦力发生了变化，因此计算得到的流速和水深随之改变。DynaRICE是二维模型，所以不存在竖向的运动。这使得两个模型在初始阶段出现结果上的偏差。当水位逐渐稳定后，这种情况便会消失，结果自然与之相吻合。

根据前文对明渠和有冰盖暗渠两种情况下曼宁公式的理论分析，可以求得在明渠的状态下正常水深hw=0.59 m；在有冰盖的情况下求得的冰下水深dw=0.73 m，加上冰盖部分的影响，最终的正常水深hw=0.91 m。由本文模型计算得到的最终正常水深为0.86 m，与理论分析对比得误差为5.49%。对于流速分布，由于冰盖底部及河床处的摩擦力的影响，冰下水流速度沿水深方向并非均匀分布，并且在冰盖层内也有水流通过，而本文模型中的二维水力模型部分是将竖向的流速平均化处理，因此这里只能将模拟结果中沿竖向平均流速（包括冰盖内部的流速和冰盖下的流速）与理论分析结果中的平均流速做对比。模型计算结果中正常水深位置的平均流速为0.37 m/s，理论分析结果中的平均流速为0.35 m/s，对比得到误差为5.71%。由于本文模型考虑了冰盖中的水流流量，而在理论分析中较难考虑到总流量在冰盖中及冰盖下的分配比例而忽略了冰盖中的流量，因此计算模型和理论分析存在较小误差是在可接受的范围之内。

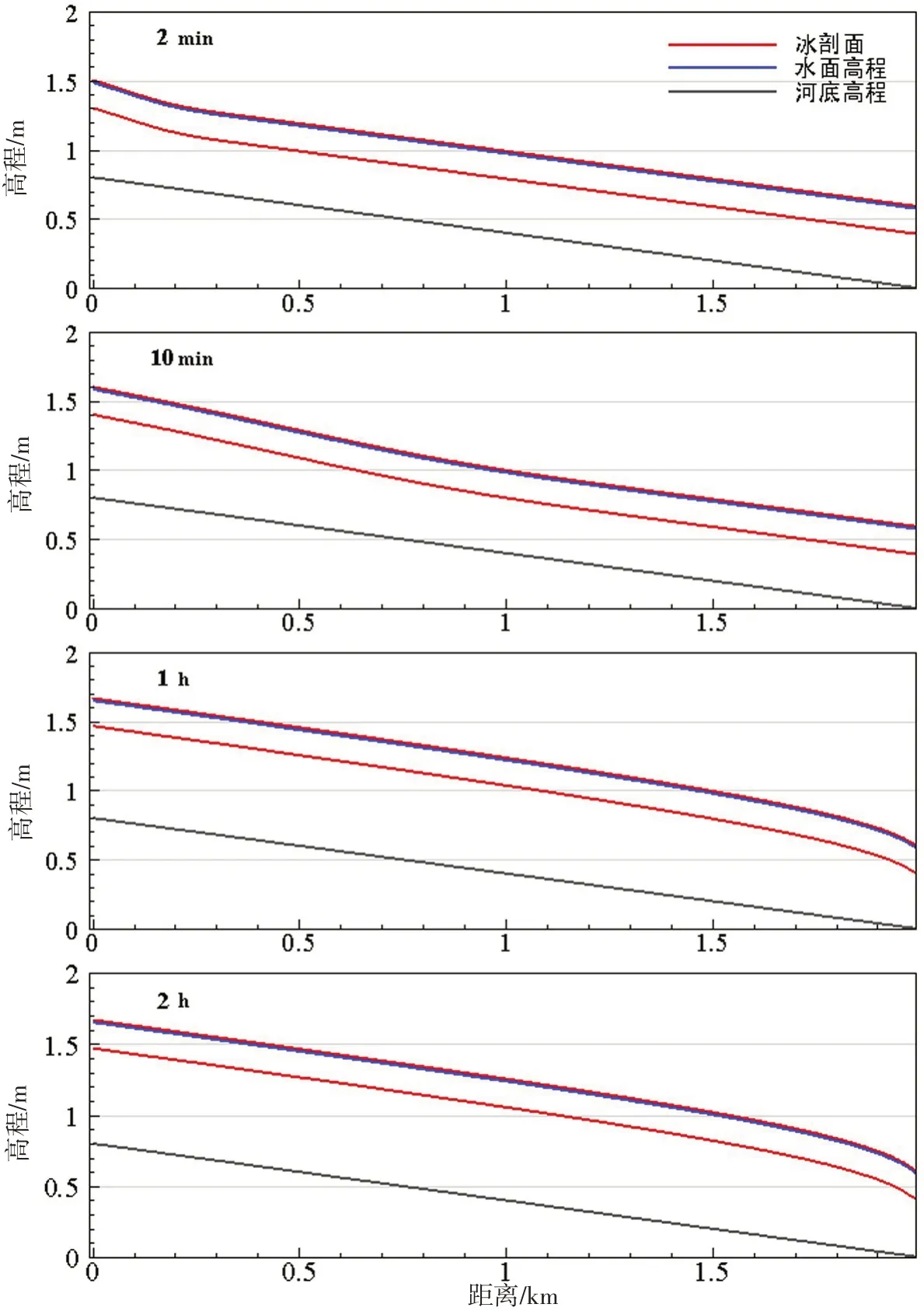
图9 封河水位抬升过程模拟结果

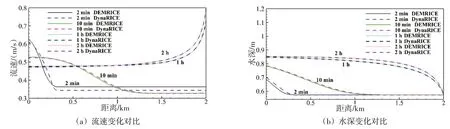
图10 本文模拟的流速和水深变化同DynaRICE结果的对比

4 河冰输移、堆积及冰坝形成过程的数值模拟

河冰的动力过程往往伴随着水力条件的快速变化，特别是在冰块堆积、堵塞河道并形成冰坝时，过水断面急剧减小，上游水位迅速升高。通过对河冰输移、堆积、阻塞形成冰坝过程的数值模拟，检验本文河冰动力学模型的有效性。

将河道调整为长度L=2000 m，宽度Bc=6 m。在河道x=700 m 的位置处设置拦冰栅，初始时刻在拦冰栅前方距上游边界600～700 m的位置生成了100 m长5.8 m宽的连续流冰区域。冰块的平均尺寸为0.1 m2，面密集度为0.8，冰厚为0.1 m，冰块之间的间隔在0.08 m左右，冰块的总数量为4060个。为保证冰水作用引起的水力变化不会影响到河道边界，在冰区距离上下游边界都留有一定长度的开阔水域。计算参数采用表1中的数值，上游边界设定恒定流量Q=9.45m3/s，下游边界设定恒定水深h=1.60m，流速为1.12m/s左右。初始的冰块分布及相关变量如图11所示。

河冰在外力作用下向下游运动，遇到冰栅后开始聚集堆积。数值模拟的河冰动力过程为20 分钟，对整个过程的模拟结果如图12所示。河冰的初始密集度为0.8，相互间有一定间隙，如图12（a）所示。当冰块遇到拦冰栅后，开始在拦冰栅前方聚集。随着上游来冰的增加，下游冰块承受的压力越来越大并开始相互挤压。靠近拦冰栅的冰块由平铺水面被压至倾斜或直立。冰块在水流动力作用以及冰块相互挤压作用下发生进一步挤压，开始形成水下塞体，河道断面过水能力下降，上下游水位开始变化，如图12（b）。随着来冰量的增加，对冰坝头部的作用力进一步加大，更多的浮冰块被挤入水下，冰坝的厚度快速增加，如图12（c）。由于过水断面进一步缩小，河道蓄水量进一步增加，上游水位也明显抬高，下游水位明显降低，如图12（d）（e）所示，此时冰坝堆积厚度已基本达到稳定状态，冰坝开始向上游延伸发展。

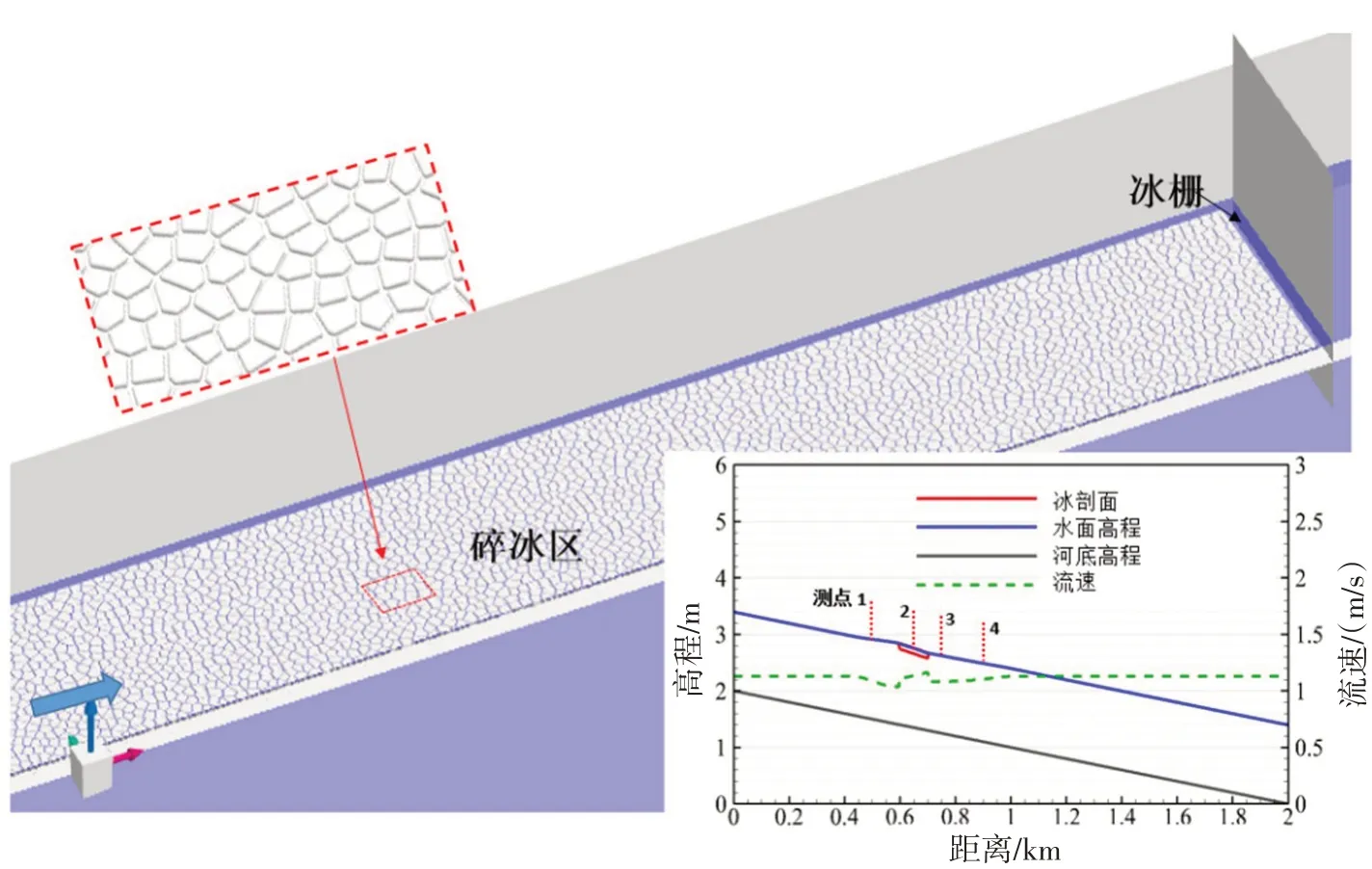
图11 初始河冰分布以及相关变量

图12 河冰堆积过程的离散元模拟结果

离散元法在计算中考虑了各个冰块所受的作用力及运动状态的变化。在冰坝形成过程的模拟中，模拟结果重现了冰坝形成稳定后河道表面冰的三种不同的分布状态，如图13所示。靠近拦冰栅的区域，称为立封区，冰块呈竖直交错、杂乱重叠的堆积状态。该区域承受着上游冰区的挤压，是整个河道内力最高的区域，冰块间相互作用最严重。该位置水流速度最大，水流对冰的拖曳作用最强，同时此处也是上游高水位区向下游低水位区过渡的区域。水面坡度大，水面梯度力也最大，从而加剧了冰块之间的挤压。在冰区的中部，冰块平铺于河道，排列紧密，相互接触但不重叠或者略微重叠的状态，称为平封区。此处属于冰内力较小的区域，外力使冰块紧密排列但又不足以使冰块重叠翻转和堆积。在冰坝尾端，冰块密集度比较低，呈自由漂移状态，排列较为稀疏随机，称为冰块的稀疏区。此处的水面由上游的正常水位过渡到冰区的水位稍稍有升高的趋势，即水面梯度指向河道上游，重力分量指向上游在一定程度上平衡了水流的拖曳作用，使得冰自由漂移在冰坝尾部。图14是稳定冰坝的冰坝剖面与水力要素的沿程分布情况。由图可见在冰坝体最低处过水断面面积急剧减小，流速急剧增大，达到3 m/s，弗劳德数也达到了最大值1.5。在冰盖前缘处的弗劳德数和流速分布为0.15和0.7 m/s。在冰坝上游端至中部x=0.68 km处，弗劳德数处于0.17左右，流速稳定在0.75 m/s，河面冰区分布状态为冰坝头部的自由漂浮和冰坝中部的平封状态。在x=0.68 km 至下游冰坝头部冰厚逐渐增大，流速和弗劳德数也快速增加至最大值，这时的表面冰状态也由平封状态过渡至杂乱交错的立封状态。由于本文尚未考虑冰盖前缘的复杂流场以及使冰块下潜翻转的作用力，因此这里平封立封过渡的临界弗劳德数和临界流速与前人研究结果相比数值偏大［45-46］，只能反映冰坝形成后沿程水力要素的变化趋势。

图13 河面上河冰的三种分布状态

图14 冰坝剖面与水力要素的沿程分布情况

模型计算了冰坝形成过程中拦冰栅受到的冰压力随时间的变化过程，如图15所示。在冰坝形成初始阶段，冰栅由于阻拦了大量来冰，其所受冰力快速增大。随着冰量的增加，冰栅前的冰块变得密集，并挤压河道两侧，河道两侧边界开始承担部分冰力。随着冰坝长度的增加，河道两侧承载冰力随之增大。上游来冰造成的冰力由两侧边界承担的部分增加，传递到拦冰栅的部分减少，因而拦冰栅所受冰力的增加速度渐渐变缓，最终冰栅所受冰力随冰坝形成稳定后趋于稳定。

图15 冰坝形成过程中拦冰栅承受冰压力随时间的变化

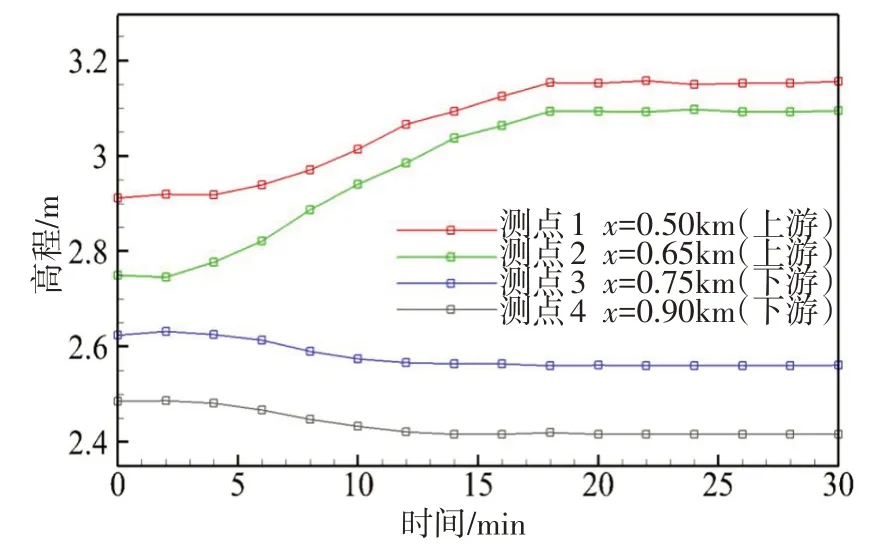
图16 冰坝形成过程中水位随时间的变化

对整个冰坝形成过程中水位的变化情况也进行了数值模拟，计算结果如图16所示。图中列出拦冰栅上游0.2 km、0.05 km处以及下游距离拦冰栅0.05 km、0.2 km处四个水位测点（具体位置如图11所示）的水位变化。从中可以看出，在冰坝的影响下，上游的水位抬升近0.24 m，而下游的水位降低近0.11 m，并且拦冰栅上游两个测点的初始水位差近0.15 m，水位抬升后水位差变为近0.08 m。由此可以看出，在冰坝的影响下，上游的水面坡降减小，水面变得缓和，而下游的水面坡降未发生很大变化。

5 结论

本文建立了河冰离散元方法与二维水动力学耦合的河冰动力学计算模型，河冰的运动过程采用离散元方法求解，河流的水动力学采用有限元方法对河冰影响下的二维浅水方程进行求解。同时采用了扩展多面体离散单元对开河时期冰块几何形状随机分布的特点进行表征。通过对明渠出现冰盖之后的水位变化过程进行数值模拟，计算结果很好地吻合了DynaRICE 的模拟结果和理论分析结果，从而验证了河冰动力学模型的有效性。在此基础上将河冰动力学模型应用于河冰输移、堆积和冰坝形成过程的模拟中。计算结果准确地描述了冰坝形成过程中河冰的运动状态以及上游水位雍抬、下游水位降低、冰下流速分布变化过程以及冰栅所受冰压力变化过程。同时再现了冰坝形成稳定后河面上冰块的分布状态，由冰坝头部的竖直交错、杂乱重叠，冰坝中部的平坦密集，到冰坝尾部的稀疏漂浮，与现场观察现象相吻合。结果表明，该模型可以准确地从细观角度表征河冰在输移聚集堆积过程中复杂的运动情况，并可准确地获得河渠内水力条件的变化过程。本文所建立的河冰动力学模型为分析河冰的动力演变过程提供了一种有效的数值方法。然而，现阶段计算模型仅仅通过与理论分析和DynaRICE模拟结果对比的验证，还缺少与原型试验或现场实测数据的对比，这将在以后的工作中着重考虑。