基于Vine Copula函数的河湖连通水环境多因子联合风险识别研究

杨 蕊，吴时强，高学平，张 晨

（1.天津大学 水利工程仿真与安全国家重点实验室，天津 300350；2.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室，江苏 南京 210029）

1 研究背景

21世纪以来，随着我国工业化、城镇化的快速发展，水资源短缺、水生态环境恶化问题日益突出，为适应新时期水利发展的需要，我国陆续兴建了一批以水资源调配和水生态环境保护与修复为目的的河湖连通工程，如南水北调、引江济太、引黄济淀等河湖连通工程［1］。由于河湖水系连通是一个充斥着模糊性、随机性以及未确知性信息的复杂系统工程［2］，这些工程在带来社会经济效益和水生态环境效益的同时，也不可避免地带来了一定的负面效应［3-4］，如调水与洪水遭遇引起的防洪风险、调水引起的污染物转移或滞留风险等。因此，如何识别与管控河湖水系连通潜在风险，实现科学、高效、安全的连通运行管理，以减少连通过程各种潜在损失，是亟需解决的技术难题。

近年来，日益突出的环境污染问题对生态系统及国民经济都造成了一定损失，使水环境风险研究得到广泛的关注。借鉴调水工程水文风险的概念［5］，本文将河湖连通水环境风险定义为由连通工程引起的区域污染物迁移和滞留等风险事件造成的损失或不利后果的可能性。对于水环境风险评价，学者们先后提出了健康评价模型［6］、随机模型［7］、灰色模型［8］、模糊模型［9］、信息熵模型［10］等以及和其它理论耦合在一起的水环境风险评价模型［11］。这些模型多用于对水体污染风险水平的衡量，在河湖连通工程环境风险评价中也有部分应用［12-15］。以上模型多应用于单一水质指标的分析，并将多项关键指标组合构成指标集对某一区域水环境状态进行整体评价，并未直接考虑各指标间的相关性。而Copula函数作为构造多变量的相关结构和联合分布的连接函数［16-18］，相较于其它模型，可以直接建立起各项关键指标的联合分布，进而对由各项关键指标超过标准限值形成的多因子联合风险进行分析［19］。但是，在使用Copula函数对多元相关结构进行建模时存在“维数灾难”的问题，且有单一Copula函数拟合效果不理想的限制，如椭圆Copula函数只能刻画对称的相关结构，三维及以上维度的阿基米德Copula函数只适合刻画变量的正相关结构［20-21］。当前Copula函数在水环境风险评价中多应用于水体富营养化评价，分析不同环境因子之间的相关性、单个富营养化因子对风险的影响程度以及构建富营养化综合评价指标等［22-24］，多应用于二维、三维。因此，如何突破维数限制，更好地评估高维变量联合风险，反映风险事件多因子相互影响并共同作用的真实特征，也是当前面临的科学问题。

本文旨在以下两个方面对现有研究做出贡献：首先，在方法上基于一种新的Copula 函数类型，即Vine Copula 函数对水环境风险多因子相关结构进行建模，并在建模过程中，通过比选15 种二元Copula（包含大部分可能的相关结构［25］）优化各变量（条件或无条件）间的相关结构，以使模型能够最恰当地刻画多变量间相关结构的真实特征；其次，在应用上以当下社会关注度较高的南水北调工程伴生水环境问题为出发点，开展河湖水系连通伴生水环境联合风险的识别研究，为进一步实现水系连通伴生水环境风险的管控提供科学依据。

2 研究方法

2.1 边缘分布拟合构建联合分布之前，须先确定各风险因子的边缘分布函数。随机变量边缘分布的经验频率采用水文中常用的Gringorten公式计算［26］：

选用6种常见的水文变量分布，即正态分布、指数分布、logistic分布、对数正态分布、伽马分布和威布尔分布，分别对各变量观测序列进行拟合，采用极大似然法评估参数，并通过AIC 拟合优度检验比选出最适合的边缘分布。AIC值计算公式［27］如下：

式中：lmax为极大似然函数值；k为参数个数。AIC值最小则拟合最优。

2.2 Copula函数Copula函数是定义在[0，1]n区间上的多维联合分布函数，它可以将多个随机变量的边际分布连接起来构造联合分布。

Sklar定理［28］：令H为n维联合分布函数，F1，F2，…，Fn为其边缘分布，那么存在唯一的Copu⁃la函数C，使得对∀x∈R n，有

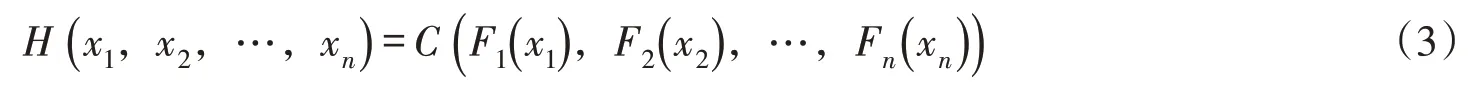
若F1，F2，…，Fn连续，则C是唯一的。相反地，如果C是一个Copula函数，F1，F2，…，Fn是分布函数，则上式定义的H是边缘分布为F1，F2，…，Fn的一个联合分布函数。

Copula 函数有很多种类型［29-31］，主要分为椭圆型和阿基米德型。表1列出了本文使用的各椭圆Copula和阿基米德Copula函数的二元分布函数表达式及其相关性质。

2.3 Vine Copula 函数当分析两变量间的相关结构时，有多种Copula 函数可供选择，例如常用的Gaussian Copula［32］、Student-t-Copula［32］、Clayton Copula［29］、Frank Copula［32］、Gumbel Copula［32-34］和Joe Copula［35］等。但一旦需要对多元相关结构进行刻画时，可供选择的Copula函数就变得十分有限，尤其对于阿基米德类Copula函数，随着维度的增加其估计和推断难度会迅速增加［21］，并且当维度达到三维及以上时只能刻画正相关结构［20］。现有研究中常用的多元Copula函数有Gaussian，Student t和Clay⁃ton Copula，但以上多元Copula 都具有一定局限性，例如Gaussian 和Student t Copula 只能刻画对称的相关结构，Clayton Copula 虽能刻画非对称相关结构，但却只存在下尾相关性［21］。因此，本文引入一种更为灵活和直观的多元相关结构建模工具Vine Copula。

表1 二元Copula函数表达式及其相关性质

Vine Copula 是由Bedford 和Cooke（2001）引入的一种具有图形结构的多变量Copula 建模函数［36］。它基于条件Copula函数和藤式（Vine）图形建模工具，利用Pair Copula将多元联合分布进行分解，从而建立起Vine Copula 模型。一般来说，n维藤结构可以由n（n-1）个二元Copula 函数以（n-1）层次树构建。每个树上有多个节点，节点之间的连线为边，而每一个节点代表的就是变量或条件变量，每一条边代表着相应的Pair Copula，最后每棵树组合在一起构成一个完整的藤结构。常用的藤结构有Cvine 和D-vine，其中C-vine 多用于拟合多变量中具有一个关键变量的情形，本文选用C-vine 进行模型构建。C-vine Copula的密度函数表达式如下：

式中，下标j表示树层级的遍历，下标i表示每棵树中节点的遍历。四维变量C-vine Copula结构如图1所示。

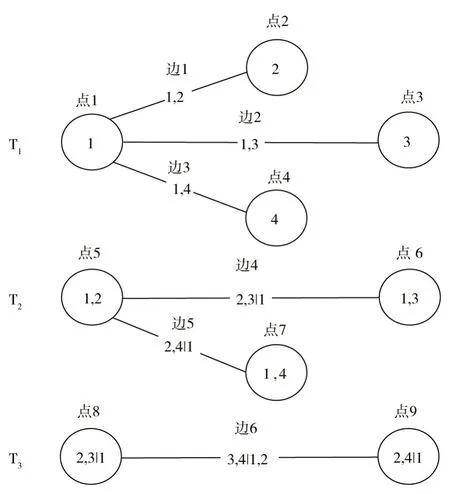
图1 C-vine Copula四维变量结构图

该方法的优势在于，相较于传统多元Copula函数，其在构建联合分布函数时不仅可以将各变量的边缘分布函数与相关结构分开建模，并且允许多个变量两两之间的相关结构有所不同［21］。由于不同的Copula 函数代表着特定的相关结构，在选取Pair Copula 函数时，本文从包含大部分相关结构的15种Copula函数中，选择最为恰当的Copula函数来刻画变量（条件或无条件）间的真实相关结构，所构建的联合分布函数比传统的多元Copula函数更具灵活性［21，25］。

2.4 C-vine Copula模型构建及验证计算多个变量两两之间的Kendall系数，将与其它变量Kendall系数绝对值之和最大的变量作为中枢变量［21］。根据AIC准则，从表1所列出的二元椭圆Copula、阿基米德Copula以及Clayton、Gumbel、Joe Copula 旋转90°、180°、270°共15个Copula函数中，分别比选出最佳的Copula函数作为第一层树（T1）的中枢变量与其它变量之间的Pair Copula，并通过贝叶斯估计方法估计出T1中各Pair Copula密度函数的参数值。利用T1所估参数生成T2各变量的观察值，并重复建立T1的过程，可得到T2最优Pair Copula类型及密度函数的参数值。重复以上过程直至最后一层树建立完成［25］。最后利用极大似然估计对藤结构中每个Pair Copula函数的参数估计进行修正［37］。

指定的分布模型能否很好的拟合变量的实际分布，对Copula函数能否正确的描述变量间的相关性结构至关重要，因此要建立分布的检验和拟合度评价。常见的评价方法主要分为图解法和解析法，图形法相对于解析法比较直观，解析法可以量化拟合效果。本文以箱型图的方式，对变量间的原始Kendall系数和模型所得变量间的Kendall系数进行比对，以验证模型的可靠性［38］。

3 案例应用

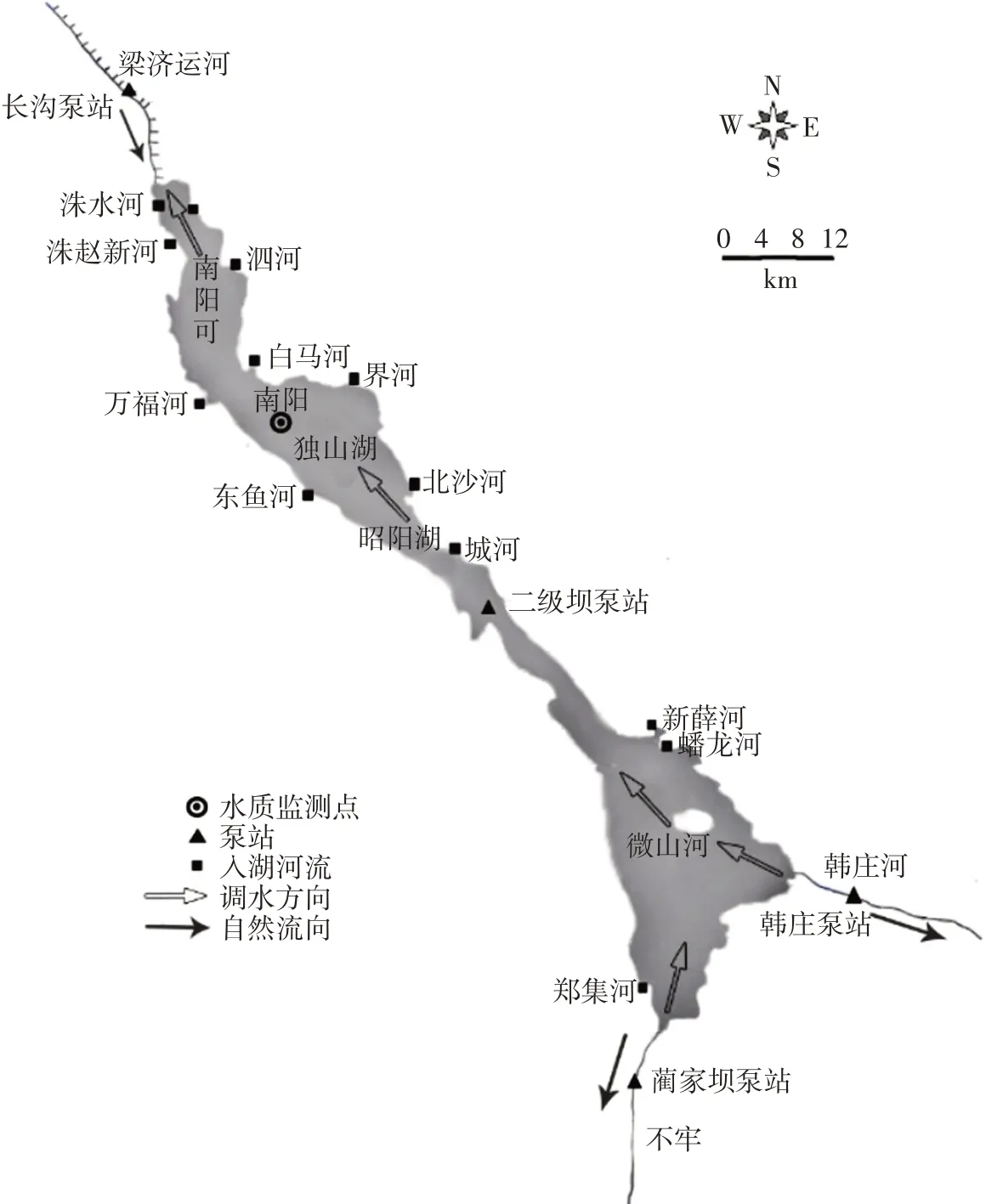
图2 南四湖水系及连通工程示意图

3.1 研究区域概况及数据来源南四湖属沂沭泗的泗河水系，是南阳湖、独山湖、昭阳湖和微山湖4个相连湖泊的总称，位于山东省西南部，自北向南流动，全湖面积1266 km2，湖泊容积16.06亿m3。作为南水北调工程东线上重要的输水通道和调蓄湖泊，南水北调东线工程的运行意味着其连通性的改变，必定引起其水环境因子的变化，区域概况如图2所示。基于指标的针对性、实用性和可行性，以及对南四湖水环境风险的综合反映能力，本文从水质指标和富营养化指标中选取代表性指标总磷（TP）、总氮（TN）、氨氮（NH3-N）和叶绿素a（Chl-a）2008—2014年月均观测数据（数据来源于南阳监测点［39］，各指标的统计特征列于表2），采用C-vine Copula函数构建四维联合分布，分别构建了南水北调东线一期工程运行前（2008.01—2013.10）和运行后（2013.11—2014.12）南四湖水环境多因子联合风险模型。结合南水北调东线工程Ⅲ类水水质要求，定义TP、TN、NH3-N浓度值劣于Ⅲ类水（Chl-a对应中营养）标准限值时为存在水环境联合风险。通过分析南四湖在工程运行前后水环境联合风险对TP、TN、NH3-N 和Chl-a 各因子敏感性的变化，提取出工程运行后联合风险的关键风险因子。之后，设置运行后关键风险因子不同风险状态组合情景，计算并分析风险发生的不利情况，识别出运行后潜在水环境联合风险。

表2 运行前/后南阳监测站水质指标统计特征表

3.2 C-vine Copula模型构建

3.2.1 建立边缘分布 表3所示为南水北调东线工程运行前、后南四湖TP、TN、NH3-N 和Chl-a 环境因子分别拟合6种理论分布所对应的AIC值，比选可得运行前TP、TN、NH3-N和Chl-a的最优拟合分布为对数正态分布；运行后TP、TN的最优拟合分布为对数正态分布，NH3-N和Chl-a的最优拟合分布为伽马分布和威布尔分布。

表3 运行前/后各变量拟合不同分布类型对应的AIC值

3.2.2 C-vine Copula模型的构建和模型检验

（1）构建C-vine Copula模型。运行前后TN与其他3种变量的Kendall'sτ绝对值之和Si最大，即表明TN 与其他3 个变量的相关性最强，将其作为中枢变量。按照上文所述模型构建方法，构建运行前、后两个C-vine Copula 四维水环境风险因子联合分布模型，模型的Pair Copula 函数选择结果及参数列于表4，模型图如图3所示。

表4 运行前/后C-vine Pair Copula的函数选择结果及参数估计

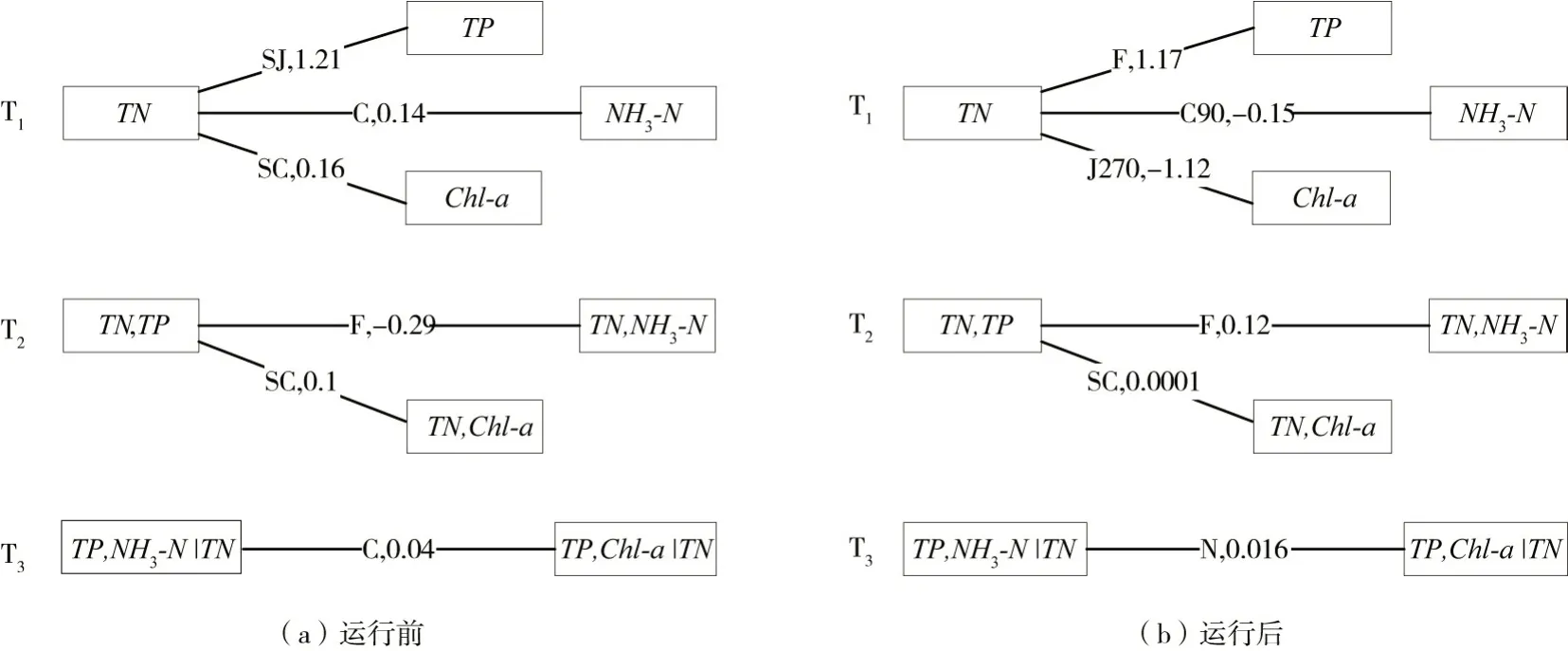
图3 运行前/后C-vine Copula四维水环境风险因子联合分布模型

（2）模型验证。将构建的C-vine Copula四维水环境因子联合分布模型中的Pair Copula类型和参数估计的结果带入仿真函数产生100组仿真数据，计算TP、TN、NH3-N和Chl-a两两因子之间的Kend⁃all 系数，循环以上步骤100 次，将100 组仿真数据所得Kendall 系数整理为箱型图，并将TP、TN、NH3-N和Chl-a各环境因子之间的原始Kendall系数标于图中。如图4所示，运行前后各环境因子之间的原始Kendall系数均落在箱型图上、下四分位数之间，并且大部分在中位数附近，说明所建立的两个C-vine Copula模型对变量的相关结构刻画较为可靠。

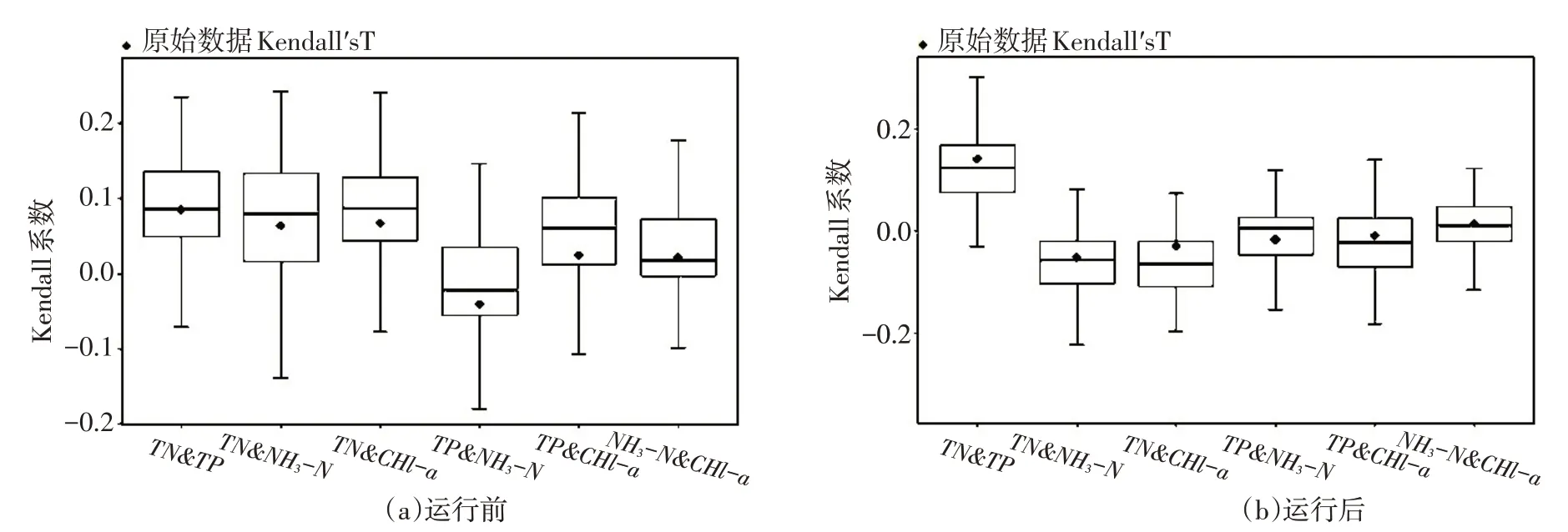
图4 运行前/后Kendall系数模型验证

3.3 风险情景设计

3.3.1 各因子敏感性分析情景 为分析南水北调东线工程运行前后南四湖多因子联合水环境风险中TP、TN、NH3-N和Chl-a 各因子的敏感性，识别出关键风险因子进而实现其风险组合分析，在完成对C-vine Copula模型的构建后，结合我国地表水环境质量标准（GB 3838-2002）及OECD（Organization for Economic Co-operation and Development）提出的富营养化湖泊（温带湖泊）营养水平划分标准，以工程运行前后TP、TN、NH3-N和Chl-a原始数据序列的均值作为基准值，分别按I—V类水对应的标准限值（Chl-a采用贫营养—超富营养标准限值）改变其中一个变量的浓度值，分析工程运行前后各环境因子对水环境联合风险的影响程度，并识别出关键风险因子。工程运行前后各因子敏感性分析计算情景如表5所示。

3.3.2 关键因子风险组合情景 由于南水北调东线工程南四湖供水水质要求为Ⅲ类水，故关键因子风险组合情景设置主要考虑工程运行后关键风险因子TN、NH3-N、Chl-a浓度值劣于Ⅲ类水（Chl-a对应中营养）标准限值时，不同风险状态（即Ⅳ类和Ⅴ类，Chl-a对应富营养和超营养）组合下的系列风险情景，从而识别出工程运行后伴生水环境多因子联合风险发生的最不利情况。具体设置如下：当TP不是关键风险因子时，其浓度值分别取工程运行前、运行后数据序列的均值（0.06/0.04 mg·L-1），TN、NH3-N分别按照Ⅳ（1.5 mg·L-1）、Ⅴ（2 mg·L-1）类水限值，Chl-a按照富营养（25 μg·L-1）、超营养（35μg·L-1）状态限值进行组合，可得到工程运行前后各6组计算工况，如表6所示。

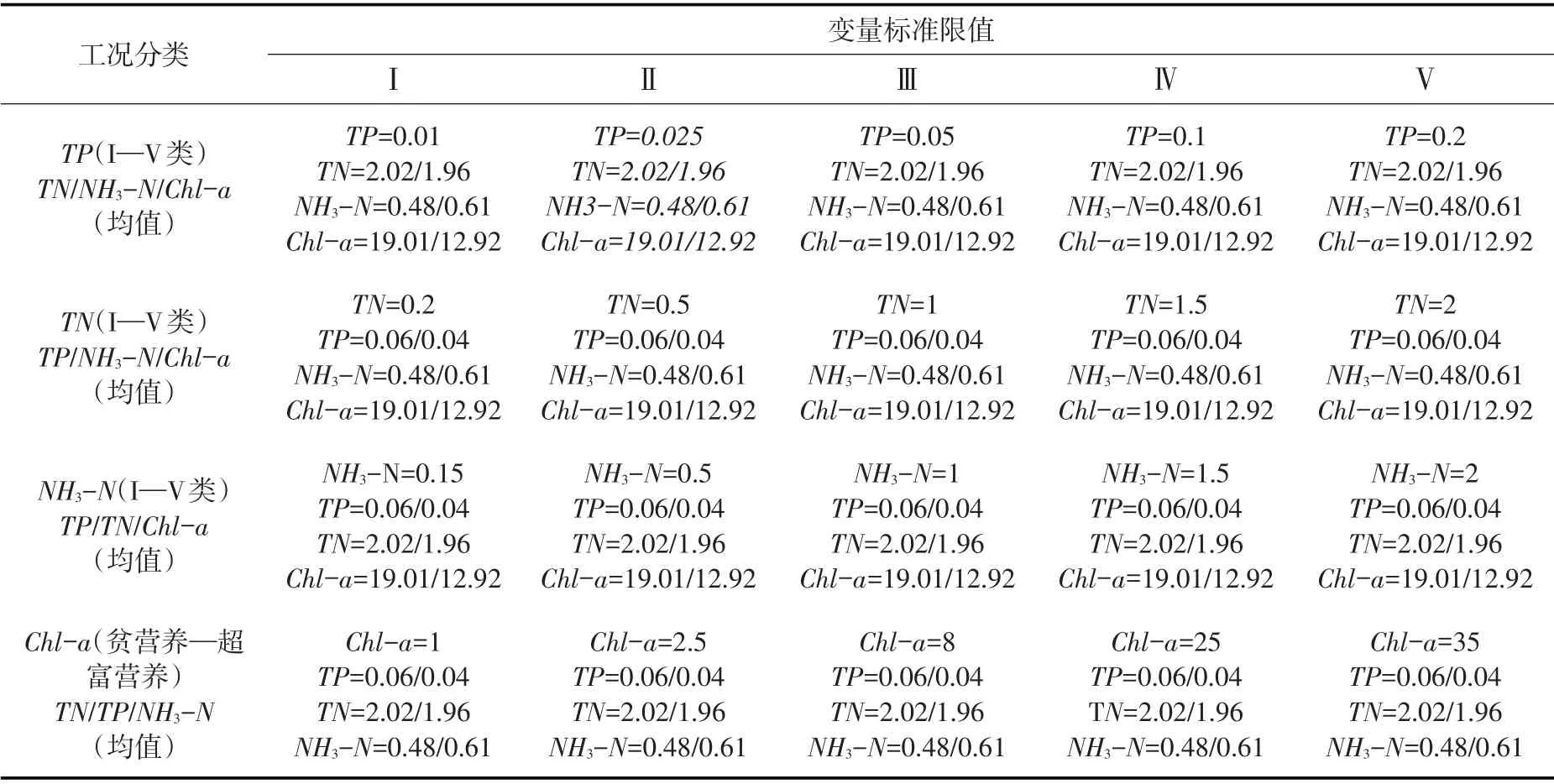
表5 各因子敏感性分析情景（单位：TP/TN/NH3-N（mg·L-1），Chl-a（μg·L-1））

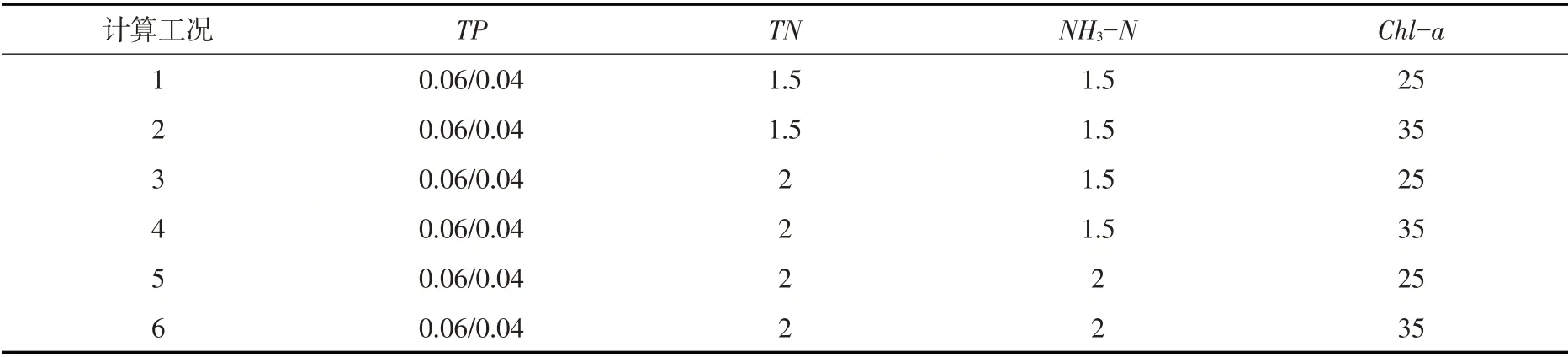
表6 关键因子风险组合情景（单位：TP/TN/NH3-N（mg·L-1），Chl-a（μg·L-1））

3.4 风险识别结果分析

3.4.1 各因子敏感性分析结果 由表2可知，工程运行后TP、TN、Chl-a浓度值均有所降低，TP由Ⅳ类水变为Ⅲ类水；NH3-N浓度略有上升，由Ⅱ类水变为Ⅲ类水。总体上，南水北调东线工程运行后南四湖南阳站处水质有所改善，与已有研究结果一致［40］。

采用四维水环境因子联合分布的概率密度值分析水环境联合风险对各因子的敏感性，在各因子处于同一分类标准限值时，其所对应的联合分布概率密度值越大，说明该因子对联合分布的变化率影响越大，即联合风险对其越敏感。由图5（a）可见，当TP、TN、NH3-N和Chl-a分别为Ⅳ、Ⅴ类水（Chl-a对应富营养和超营养）限值时，各因子对应的联合分布概率密度值相对其他工况均较大，但各因子之间的差别较小，说明各因子对于联合风险均较为敏感，其中最敏感的因子是TP，NH3-N 次之。对比工程运行前（图5（a））和运行后（图5（b）），在Ⅳ、Ⅴ类水（Chl-a 对应富营养和超营养）工况下，运行后各因子联合概率密度值均有所降低，说明南水北调东线工程运行后，水环境联合风险对TP、TN、NH3-N和Chl-a的敏感性均有所降低。其中TP敏感性变换最大，从最敏感的因子变为敏感性最弱的因子，敏感性减小幅度较大，可将其从关键风险因子中排除；而TN、NH3-N、Chl-a 概率密度值相近且较运行前减小幅度不大，因此，认为这3个环境因子是工程运行后水环境联合风险的关键因子。

为进一步分析运行后模型中各变量对概率密度的影响，比对运行后模型在运行前20组工况和运行后20组工况下的概率密度结果。运行前和运行后20组工况的区别在于各变量的均值不同，运行后工况中各变量均值除NH3-N升高外，其它3个变量均有所降低。如图5（c）、（d）所示，TP在Ⅰ—Ⅴ级时，运行后工况概率密度较运行前各工况呈现增大后减小趋势，并在Ⅲ-Ⅳ级时出现极值点，说明Ⅰ-Ⅲ级时TN、NH3-N、Chl-a相较于TP发挥主导作用，后者在Ⅳ-Ⅴ级时发挥主导作用。TN在Ⅰ—Ⅴ级时，概率密度始终呈现上升趋势，可认为TN 始终对概率密度的影响较大。NH3-N 处于I 级时，当其它3个变量浓度值降低，概率密度降低，但从Ⅱ级便出现上升趋势，说明NH3-N对概率密度的影响跨度最大。Chl-a 在Ⅰ—Ⅴ级时，概率密度呈现降低后升高走势，并在Ⅲ-Ⅳ级之间出现极值点，说明Ⅰ-Ⅲ级时TP、TN、NH3-N 相较于Chl-a 发挥主导作用，而随着Chl-a 浓度的增加，其在Ⅳ-Ⅴ级时发挥主导作用。

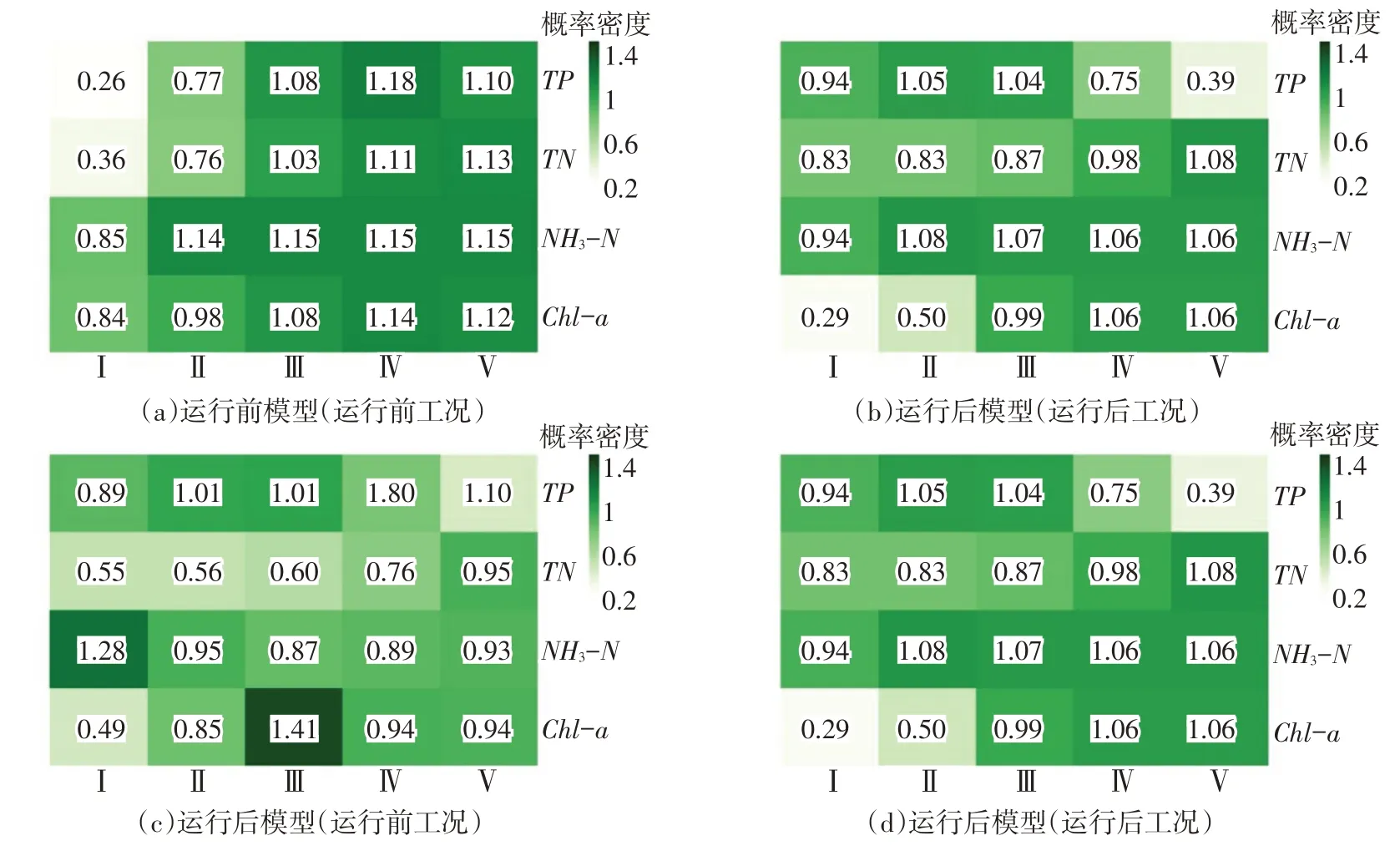
图5 运行前/后模型（联合分布）不同工况下的概率密度值

同时，应用传统多元Copula函数构建四维水环境因子联合分布，即椭圆Copula函数：（1）Gauss⁃ian Copula，（2）Student-t-Copula；阿基米德Copula 函数：（3）Clayton Copula，（4）Frank Copula，（5）Gumbel Copula。通过联合分布概率密度值分析水环境联合风险对各因子的敏感性，并与Vine Copula函数计算结果进行比对，得到椭圆族Copula 函数计算结果（1）（2）相似，阿基米德族Copula 函数（3）（4）（5）计算结果相似。对比工程运行前和运行后的计算结果，在IV、V类水（Chl-a 对应富营养和超营养）工况下，二者均能排除TP为关键风险因子，与Vine Copula 函数计算结果一致；但是，运行后随着NH3-N、Chl-a 浓度值增大，传统多元Copula 函数的联合分布概率密度值始终为零，无法反映NH3-N、Chl-a为关键风险因子。具体分析可能存在两方面原因，一是由于椭圆Copula函数只能刻画对称的相关结构，而不同变量间的相关关系并非都是对称结构；二是在计算过程中由于阿基米德Copula函数只能刻画变量间的正相关结构，在拟合负相关变量时会以零值覆盖负值Kendall系数，进而影响Copula函数参数的计算，致使模型拟合效果失真。受文章篇幅限制，未将对比结果图列于正文中。

3.4.2 关键因子风险组合情景结果分析 基于各因子敏感性分析结果，计算了关键风险因子TN、NH3-N、Chl-a 不同风险状态组合下6 种工况在南水北调东线工程运行前后的联合分布概率密度值，结果如图6所示。由图6坐标定义可知，若计算工况所得值处于对角线上方则说明运行后联合分布的概率密度值大于运行前概率密度值，且距离对角线越远说明二者差异越大，即该工况下运行后风险变化速率越大，响应时间越短。对比工况（1，2）（3，4）（5，6）（括号中第二工况相对于前一工况仅Chl-a浓度值由富营养变为超营养）计算结果可知，随着TN、NH3-N、Chl-a浓度的增加，相应工况的计算结果距离对角线越远，说明各因子浓度越大时，运行后该浓度值下的联合风险变化速率越大，即不确定性越大。其中，工况1，即TN和NH3-N为Ⅳ类水标准限值、Chl-a为富营养状态限值时，运行前后四维水环境联合风险变化不大；而工况6是运行后四维水环境联合风险最不利的状况，即TN和NH3-N达到Ⅴ类水标准限值、Chl-a为超营养状态（35 μg·L-1）时，运行后水环境联合风险变化速率增幅最大，不确定性提高，需要及时响应。同时，由于运行后模型中TN、NH3-N对概率密度的影响范围较其它变量更大，建议重点关注TN和NH3-N指标。

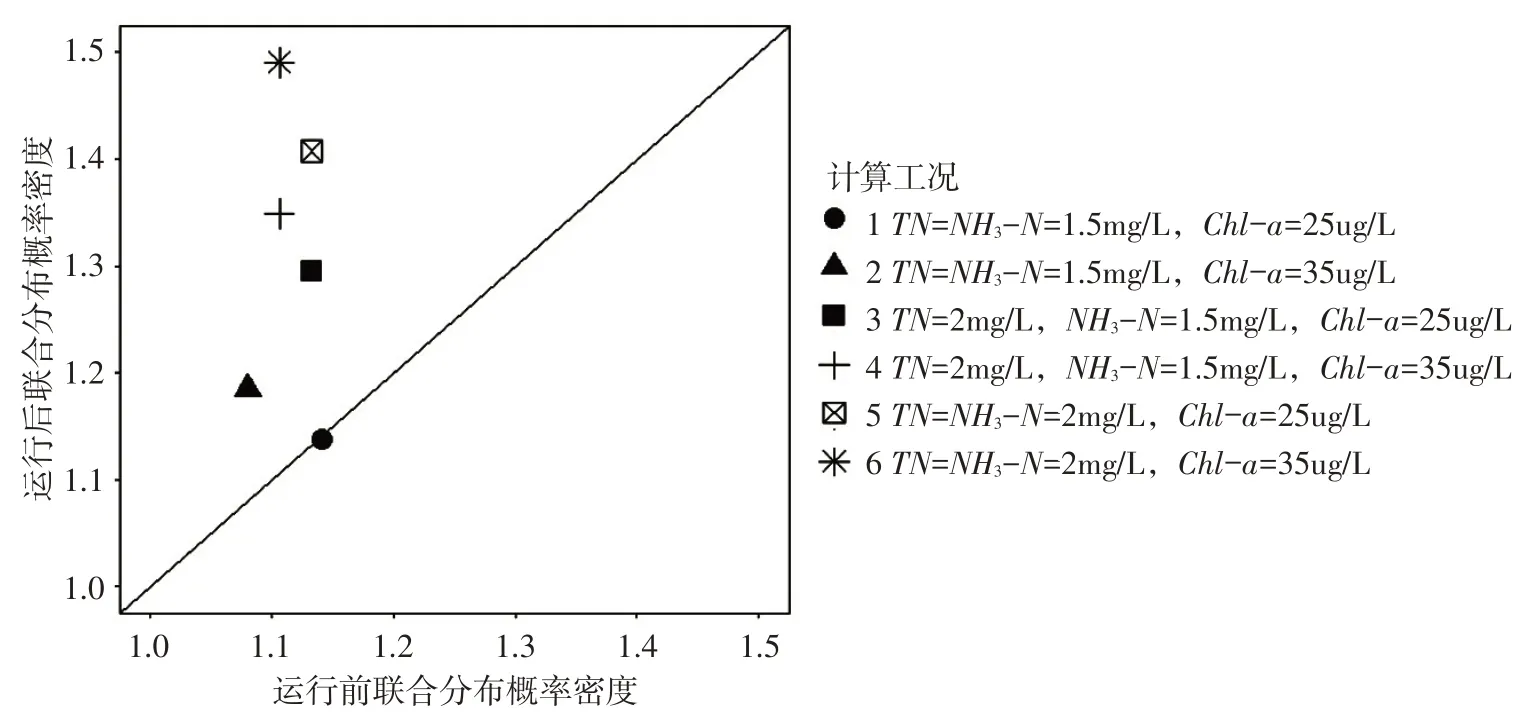
图6 运行前/后关键因子风险组合情景联合分布概率密度值

4 结论

（1）本文构建了一种基于Vine Copula函数的水环境多因子联合风险模型，该模型避免了构建多变量联合分布函数时各边缘分布不同的问题、二元Copula 函数“维数灾难”的问题以及单一多元Copula函数对两两变量间相关结构刻画失真等弊端，能够较好地综合多风险因子，为水系连通伴生水环境风险识别提供可行的技术方法。

（2）将所构建的多因子联合风险模型应用于南水北调东线工程运行后南四湖水环境联合风险的识别，得出以下结论：南水北调东线工程运行后，当TN和NH3-N达到V类水标准限值、Chl-a为超营养状态（35 μg·L-1）时，南四湖水环境联合风险最不利，发生联合风险的可能性和速率较工程运行前大幅增加，需及时采取措施。建议重点关注TN和NH3-N指标。

（3）在本文工作基础上，进一步研究可在以下方面拓展：增加考虑水质指标项目及数据序列长度，以提高各因子之间的相关性；探讨其他Vine Copula函数的适用性；考虑实际变量间的结构动态性与Vine Copula模型的耦合关系。