多体接触问题面面接触算法研究

李广凯，刘传东，肖仁军，马怀发

（1.山东泰山抽水蓄能电站有限责任公司，山东 泰安 271000；2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038；3.中国水利水电科学研究院 工程抗震研究中心，北京 100048）

1 研究背景

接触问题是工程中普遍存在的力学问题，接触问题的特点和难点是接触边界和接触力的未知性。由于接触界面的区域大小、位置以及接触状态都是未知的、随时间变化的，因此接触问题表现出显著的非线性特征。接触问题的非线性决定了接触分析过程中需要经常插入接触界面的搜寻判定。有限元法为分析接触问题提供了有效的工具，在进行有限元求解接触问题时，接触体被离散为空间单元集，接触界面的相互作用被转化为离散的单元表面之间的作用或者离散的节点与单元表面的作用。接触问题的动力分析主要包括选取时间积分方案和接触算法，其中接触算法包含接触搜索算法和接触力算法。

接触搜索的目的是确定整个系统中有哪些部位发生了接触或者有哪些原已接触的部分发生了滑移或脱离。在接触动力分析中，接触搜索占较大的计算量，因此接触搜索算法的计算效率至关重要。由于接触搜索是接触力计算的基础，所以其计算精度也非常关键。在一般情况下接触搜索需要先进行全局搜索，再进行局部搜索。通过全局搜索先粗略找到围绕特殊点所有潜在可能的接触单元面。全局算法有主从面算法［1］、级域算法［2-3］、单曲面算法［4］、位码算法［5］和LC-Grid法［6］等。主从面算法将相互接触的两个边界面分别指定为主面和从面，主面上的节点定义为主节点，从面上的节点定义为从节点，但在单一曲面发生严重形变时，不能处理自接触搜索；级域法［2-3］涉及不同级别接触元素的定义和管理，在接触搜索过程中需要逐级进行，数据管理复杂，不便于并行计算，并且只在一定的条件下有效。单曲面算法［4］使用了子域排序算法来寻找接触面，通过三层嵌套排序来完成三维空间的搜索过程，优点是能够处理自接触问题，但该算法编程复杂，运算量大，可并行性差；位码算法采用了位码构造思想，将三维空间中分类和搜索的问题转化为一维数组分类排序，进行搜索处理，既不需要事先指定接触区域，又避免了三维嵌套搜索，便于进行大规模计算，是计算效率较好的接触搜索算法；LC-Grid类似于位码算法，其计算时间和存储要求与接触面数量成线性比例，但计算效率依赖于接触空间分解尺度。

局部搜索目的是计算节点到单元面的精确距离，找出接触投影点所在单元面的相对位置关系，从而确定接触节点与单元面间的接触状态。局部搜索算法主要有点面算法［1，4］、小球算法［7］、基于光滑曲面的搜索算法［8-9］以及内外算法［10］等。点面算法在计算“点”在单元面上的投影点时，需迭代求解点面投影的偏微分方程，有时会出现迭代稳定性问题；小球算法是一种几何近似方法，该方法将小球嵌入表面单元，仅对小球施加不可侵入条件，主要用于滑动和摩擦力不是至关重要的问题；基于光滑曲线（曲面）的搜索算法采用样条函数逼近接触表面更加准确地描述接触边界，从而使接触搜索甚至接触力的计算精度提高，但此技术在离散模型中引入了冗余信息，加大了数据处理的难度；内外算法仅仅是逻辑操作过程，简单稳定，计算精度高。但这些方法几乎都出现搜索盲区问题。另外，除内外算法外，其它算法都需要通过点到投影面的非线性投影方程，确定节点和潜在接触面的距离。尽管小球算法可以回避求解非线性方程，但会降低计算的准确性。

在完成接触搜索之后，接触力求解通常采用拉格朗日乘子法或罚函数法［11］引入附加条件构造修正基本方程泛函的方法。其中罚函数法需要根据经验选择接触刚度参数即弹簧常数，而拉格朗日乘子法对接缝的处理更真实、更自然。接触面的本构模型按照接触面的性质，有光滑接触模型和摩擦接触模型，如果接触面是绝对光滑的或摩擦可以忽略，则采用光滑接触模型，但在处理坝体伸缩缝和地基夹层接触时，一般采用摩擦接触模型，并按库伦摩尔准则考虑摩擦条件。

强震作用下的高混凝土坝系统灾变过程伴随着材料和接触复合非线性问题，对其进行全过程精细化数值模拟和全面深入的抗震安全评价，需要求解未知量高达百万甚至千万级，尽管各种商业软件在求解一般常见问题时可以显示出所谓的强大功能，但在计算方法和计算实施方案上很难适用于解决高混凝土坝复杂工况下地震响应分析所遇到的复杂而又特殊的问题，因此，高性能并行计算是解决该问题的必然选择。

本文拟在研究现有接触算法的基础上，提出多体接触问题快捷高效的面面接触算法。这种算法既可解决搜索盲区问题，又能回避求解非线性投影方程。本文算法采用拉格朗日乘子法动力接触方程的增量形式求解接触力，另外，为了便于并行计算及其程序编制，本文还根据接触面分布特点进行预分区处理，并基于提出的多体接触问题面面接触算法，开发实现其算法的FORTRAN 源代码程序，为后续实现高混凝土坝和岩体高边坡静动力分析的并行计算提供支持。

2 搜索算法分析

2.1 全局搜索算法本文将主从面算法与位码算法相结合，实现接触面的全局搜索。利用主从面算法［1］在建立几何模型时，根据可能接触边界的分布特点将可能接触边界面分别指定为主面和从面，并将其定义为“接触面对”，再利用类似于位码算法［5］将包含模型接触表面的三维空间划分成若干个立方格，并对这些立方格在三个纬度方向进行整数编码，通过这些位置号码从三维映射到一维，基于一维排序和搜索的算法来实现对区域内接触节点的检测判别。在有限元剖分网格时主面单元上的节点定义为主节点，从面单元上的节点定义为从节点。通过搜索与主面接触的从节点，即找出由从节点与主面上的单元面所构成的“接触点面对”。

本文构建了描述“接触面对”的主面单元和从面单元的共享实常数组：主面单元用正整数表示，从面单元用其对应的负整数表示，当绝对值相同时主面单元和从面单元构成“接触面对”；不同的“接触面对”通过不同的实常数定义；一组实常数可以对应多个边界面。

以下是对一组“接触面对”的全局搜索步骤：（1）搜索预处理：统计“接触面对”单元面上的主节点和从节点个数，计算各单元面外法向量及各节点外法向量。其中节点外法向量由包含该节点的单元法向量取平均得到。（2）根据“接触面对”的位置关系，构造包含接触单元面的最小长方体。在接触问题的有限元计算过程中，全局搜索是相对耗时较大的计算环节，为了避免在每个时间步都进行全局搜索，适当扩大该长方体的区域，确定接触搜索范围。（3）确定立方格的网格尺寸，立方格尺寸与接触面中平均的单元尺寸相接近或可以稍大一些。（4）建立典型的立方格结构，其三个坐标（x，y，z）方向的网格尺寸一致。按先x方向，再y方向，最后z方向的顺序对立方格进行编号。（5）对当前“接触面对”的所有主从节点循环，根据节点坐标确定其所在的立方格的编号［14］。（6）对立方格循环，在当前立方格中，对每一个主节点，找距离与其最近的从节点，并记录该从节点所对应的接触单元编号，建立点面接触测试对。

基于以上全局搜索流程编制的程序框图如图1所示。

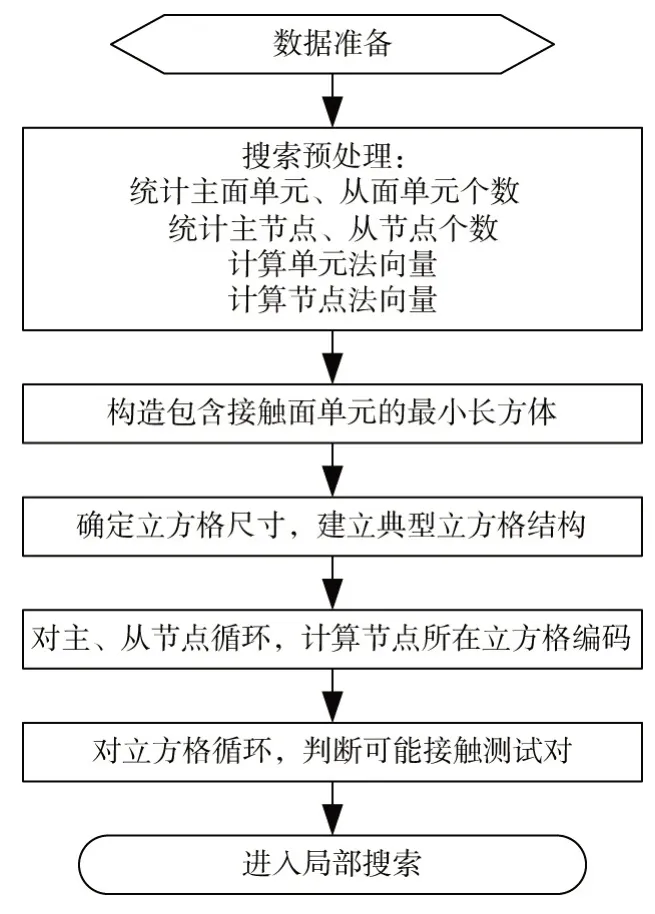
图1 全局搜索程序框图

2.2 局部搜索算法本文结合点面算法与内外算法完成接触局部搜索。由全局搜索获得“接触面对”的点面关系，采用内外算法判断“接触面对”主面上的节点落入哪些从面接触面单元内，为了避免搜索盲区，本文采用了相关单元节点法向“平均向量”。如图2所示，在接触单元中，节点B的法向量n取单元AB的法向量na和单元BC的法向量nb平均值，即判断主节点沿平均法线方向的投影点是在目标面单元的内部或外部。

下面给出一组“点面接触测试对”的局部搜索步骤：（1）对测试对中的面单元数进行循环，根据“点”法向量与单元面法向量，进一步判断是否为潜在接触关系。（2）针对潜在接触单元，计算“点”到单元面投影点位置及其贯入量。（3）由内外算法［10］，判别“点”是落入到目标单元面的有效区域的内部还是外部。（4）如图3所示，如“点”在目标单元面内部，则由三角形面积坐标法，计算投影点在单元内的局部坐标，从而得到投影点对应的单元插值形函数，进而得出接触关联矩阵。

在图3中，Vij表示由节点i指向节点j的矢量；矢量n1I=V12×V1I；n为从节点I的法向矢量；投影点x将四边形分割成4 个小区域，对应的面积为Δ1、Δ2、Δ3和Δ4，由此可以求得x的局部坐标。

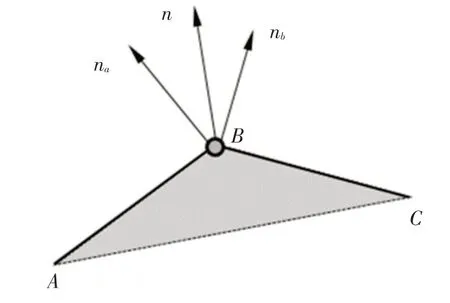
图2 两个单元的平均向量

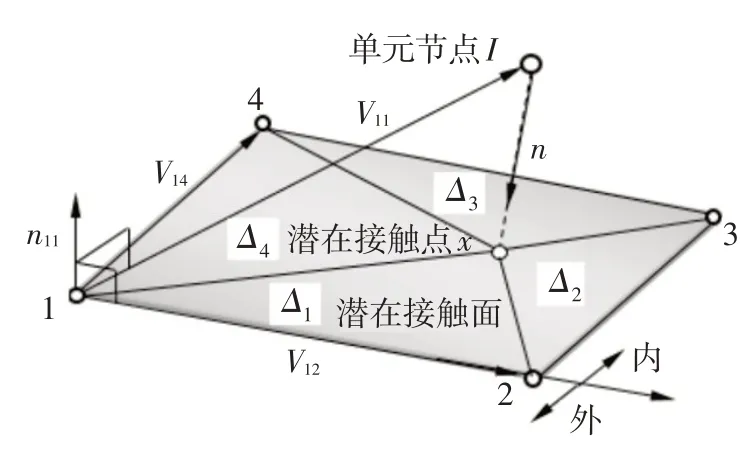
图3 点与单元面的关系

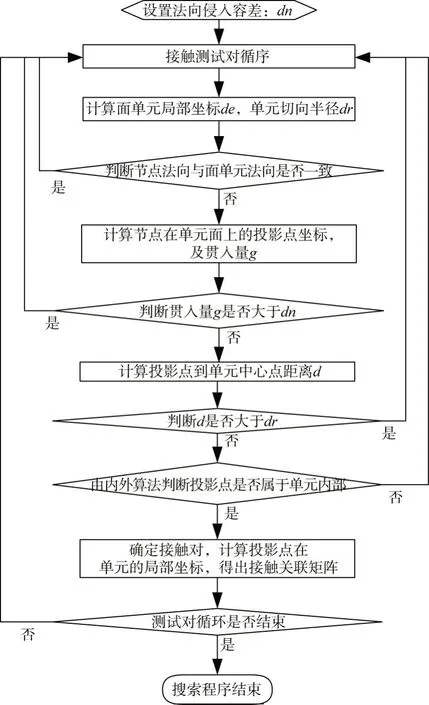
图4 局部搜索的程序

图4给出了基于局部搜索流程编制的程序框架。

综上所述，本文采用主从面算法与位码算法相结合完成接触全局搜索，点面算法与内外算法相结合完成接触局部搜索。同时在执行接触搜索前预先考虑了接触区域分块划分，使得本文算法可以方便地进行高混凝土坝和岩体高边坡静动力稳定分析的并行计算处理。

3 接触力计算

根据可能接触边界的分布特点，将计算域分解成不同的子区域。考虑由N个子区域Ωi(i=1，2，…，N)组成的多接触体系统。对于子区域i，其动力平衡方程可表示为：

式中：ρ为质量密度；c为阻尼系数；为速度分量；为加速度分量；fj为体力分量；σjk为应力张量分量。

不同子区域间的可能接触边界条件为分离状态、黏着状态或滑动状态。

接触力求解采用拉格朗日乘子法。对每一个编号为i的子区域，独立进行网格剖分和有限元离散后，在引进拉格朗日乘子λ后，动力学方程式（1）的空间离散形式为：

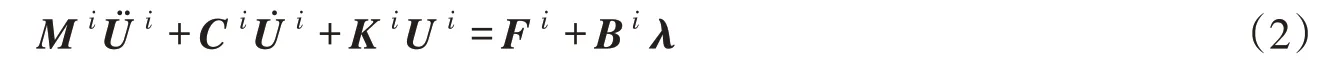
式中：i为子区域编号；M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；F为荷载项；Bi=[BinB it]为位移与接触力相关矩阵，Bin、Bit分别为接触面法向和切向相关矩阵；λ为拉格朗日乘子力（接触力）。

采用Newmark直接积分法，将式（2）写成增量形式：

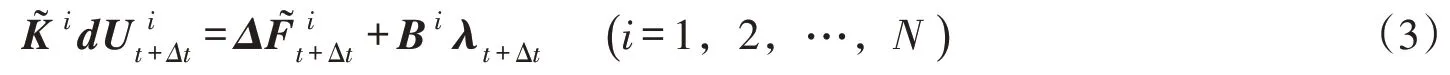
式中：为广义刚度；为广义力增量；

可能接触的边界条件的离散形式为：

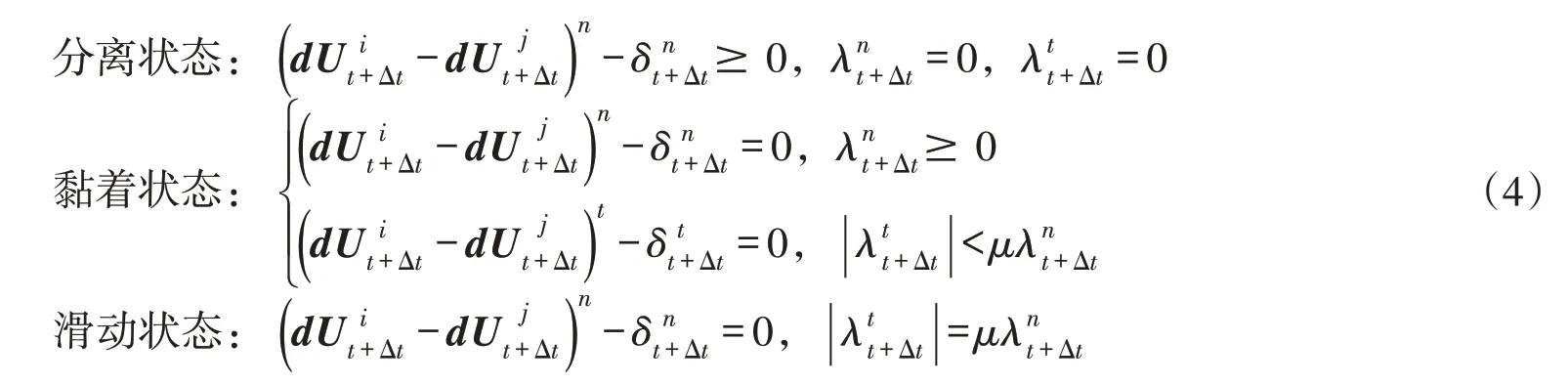
式中：δ为接触面间隙，会随着时间步变化，应根据可能接触边界的几何位置自动判定和修正，法向接触间隙切向接触间隙

将式（3）和式（4）写成整体的形式：

由式（5）消去未知量dU，整理出关于乘子力的柔度矩阵D及接触荷载向量Q：

其中：

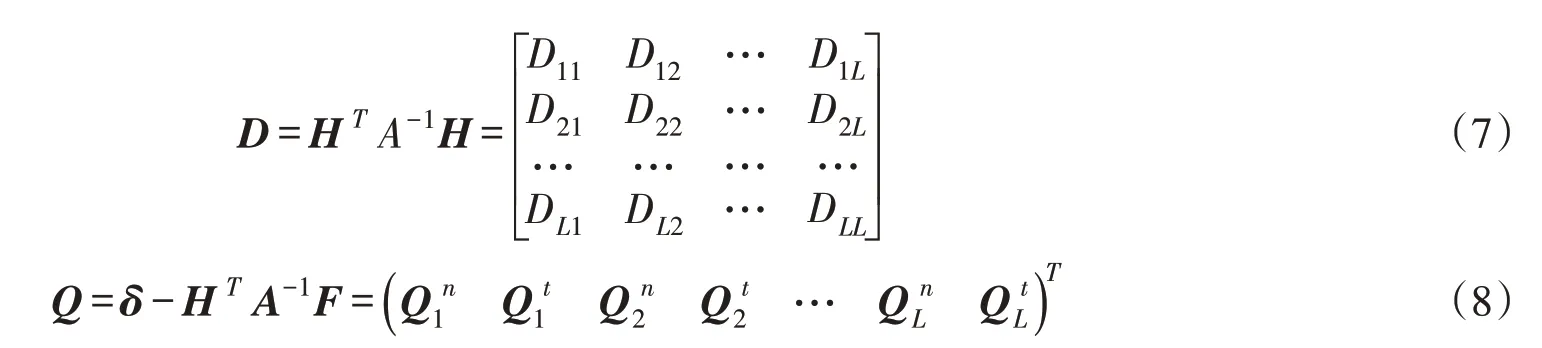
将接触力的计算转化为不等式方程组的求解：

采用拟高斯迭代法［12-13］求解t+Δt时刻位移增量与接触力。在处理位移约束边界时，将在刚度矩阵对应约束边界点所在行的对角线元素置1，并将与这个对角线元素相应行和列的其它元素都赋为0，位移方程右端赋予相应约束位移值。这样做可以避免含有边界约束的接触面形成接触力柔度矩阵奇异的问题。

4 算法验证

下面将采用两个算例验证本文提出的面面接触算法。算例选取的一般原则是模型简单典型，将计算结果与其理论解对比，再者借助于商业软件相应的功能对本文算法程序进行补充验证。第一个为块体接触模型，主要验证算法的稳定性；第二算例为经典的赫兹问题，将数值计算的接触力和接触半径结果与理论解比较，并借助商业软件考查接触面上的变形分布是否与本文算法结果是否一致，以验证本文算法的正确性和精确性。

4.1 块体接触分析考虑由两个块体组成的系统，如图5所示，块体1和块体2在x方向、y方向和z方向的长度均为100 m，块体1在3个尺寸方向均为10等分；块体2在竖向10等分，在横向两个方向20 等分。块体1 和块体2 的密度均取10 kg/m3，阻尼比取200；两块体弹性模量为10 GPa，泊松比取0，摩擦系数取0.6。块体1底面法向约束，块体2突然施加100 N/m3体积力，由本文算法程序计算其动力响应，时间步长分别取0.01、0.04、0.06和0.10 s。由本例给出的弹性参数可以得到精确解，即块体上表面的竖向位移为-1.5×10-4m，两块体接触面的竖向位移为-1.0×10-4m。

图6给出了两块体在突加重力作用下稳定后的变形云图。图6显示，最大变形位于块体2上的上表面，其竖向位移值为-1.5×10-4m。

图7和图8分别给出了位于两块体接触面块体2底面中点和上表面中点的位移时程曲线。图7和图8显示，时间步长为0.01 s 时的变形很快稳定下来，其次是步长为0.04 s，然后为0.06 s 和0.10 s。由于本文算法动力方程的时间积分采用了无条件稳定的Newmark 积分，因此，时间步长的大小仅会影响计算精度而不会影响其数值计算的稳定性。由图7和图8可以看出，在计算稳定后，接触块体2底面和上表面竖向位移值分别为-1.0×10-4和-1.5×10-4m，与精确解完全相同。

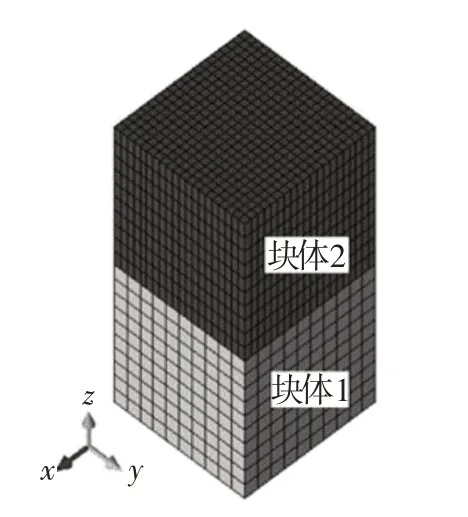
图5 块体接触模型

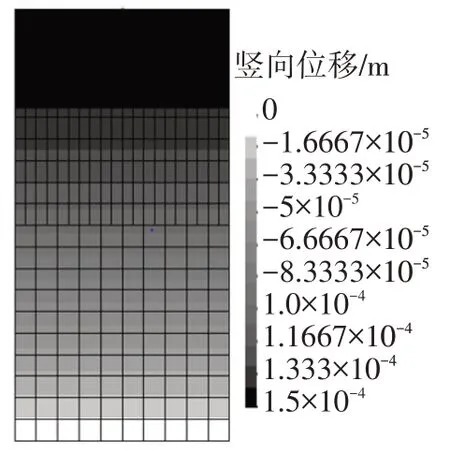
图6 接触块体竖向变形云图（单位：m）

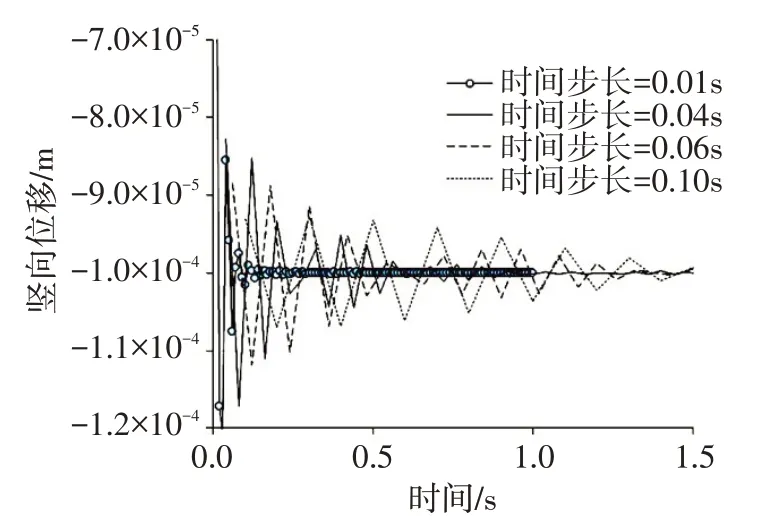
图7 块体2底面中点位移时程

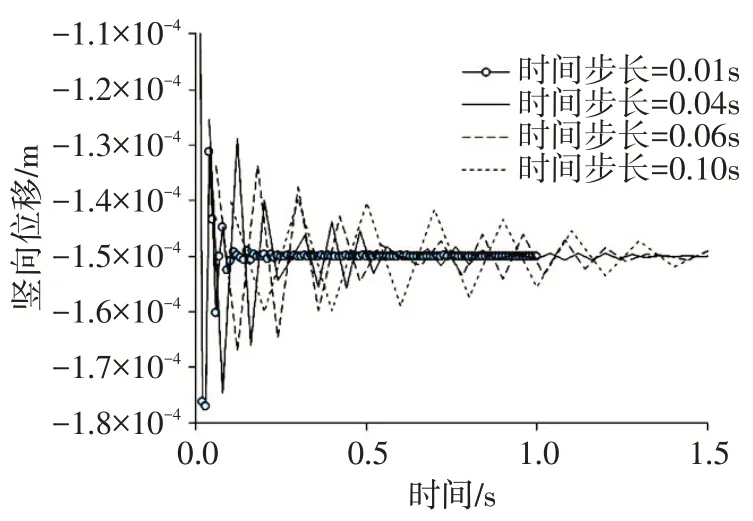
图8 块体2上表面中点位移时程

4.2 圆柱体接触分析两平行接触的圆柱体接触体［15］，如图9（a）所示，考虑其对称性，取1/4圆柱进行分析。设两圆柱体的半径均为5 mm，弹性模量为210 GPa，泊松比为0.3，认为两圆柱为绝对光滑接触，即不计接触面的摩擦力。计算模型取圆柱体长1 mm。按图9（b）所示的在底部界面施加法向位移约束，上部施加的竖向位移为-0.03 mm。模型网格划分为两种区域，计算模型网格如图9（c）所示，即接触部分的网格密度较大，网格尺寸取为0.1 mm，大约为五分之一圆柱半径区域，而其余区域的网格密度较小。密度取7.85×10-6kg/mm3，阻尼系数取200。时间步长取0.01 s，计算至时长3 s，即得到静态稳定解。

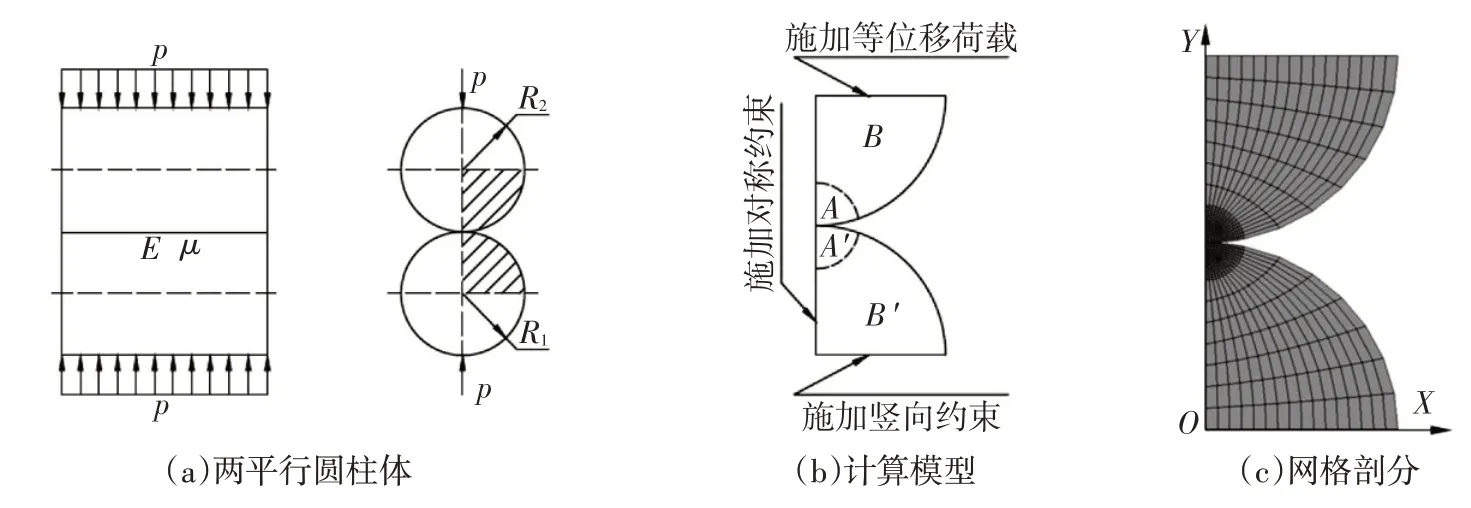
图9 两平行圆柱体的接触

在本文中，圆柱弹性模量E=210GPa，圆柱半径R1=R2=5mm，圆柱体长L=1mm，当δ=0.03mm时，由接触相对位移反求得沿圆柱轴向分布力P=1234.42N/m，b=0.185mm，σmax=4256.4MPa。

由本文算法程序得到的沿Y向的应力分量云图如图10所示，最大接触应力发生在接触中心点，其值为4136.6 MPa，与赫兹理论值为4256.4 MPa 相比，相对误差仅为0.9%；计算得到接触半径为0.188 mm，赫兹理论解值为0.185 mm，相对误差为0.6%，本文算法的计算结果与理论解几乎完全吻合。该算例结果表明，本文的接触算法是正确的和有效的。

另外，采用ANSYS软件对两接触圆柱体变形进行补充计算，得到如图11所示的两平行接触的圆柱体接触体竖向变形云图。从图11可以看出，本文算法程序与ANSYS 软件计算得到的变形分布一致。对比表1列出的沿两圆柱上下接触面由左到右的竖向位移，二者上接触面位移的最大误差为0.71%，计算结果几乎完全一致。

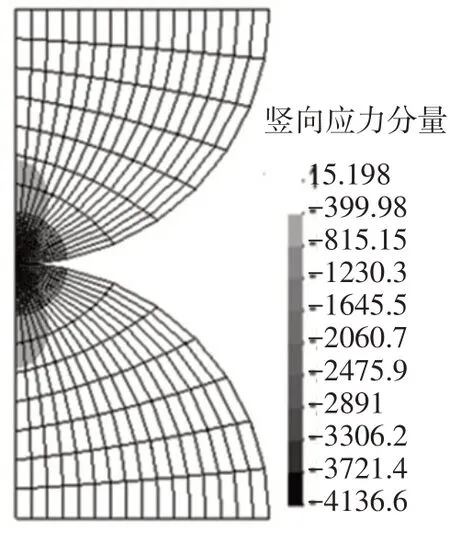
图10 本文算法计算的竖向（Y）应力分量 （单位：MPa）

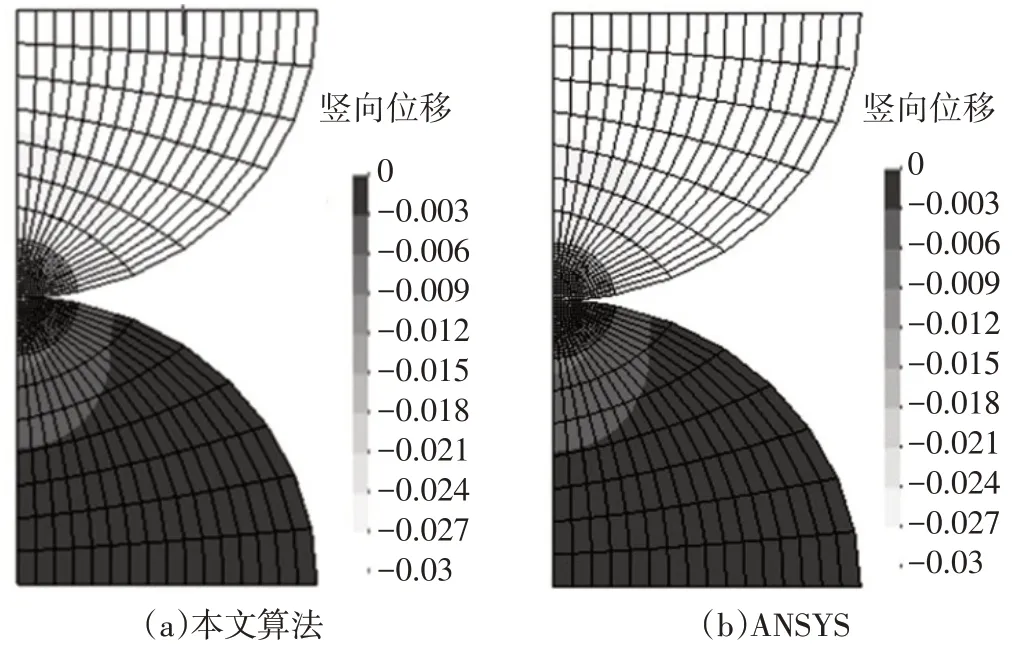
图11 两平行圆柱体接触体竖向（Y）变形云图（单位: mm）

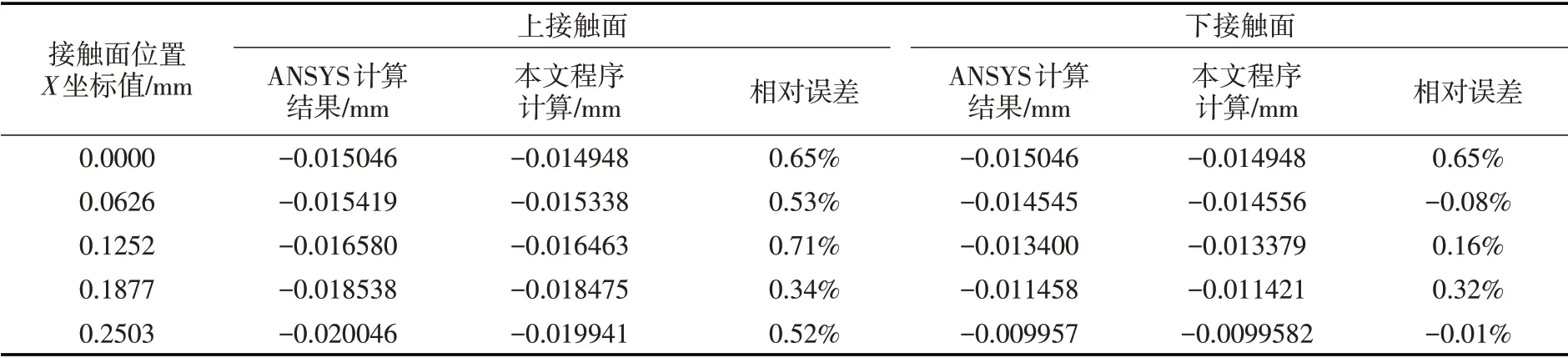
表1 圆柱接触面位置位移计算结果对比

5 讨论及结论

通常位移边界条件的引入有3种方法：（1）合成总刚矩阵时划去边界位移约束对应的各行各列元素，紧缩总刚度及荷载列阵，将约束的影响作用转移到荷载列阵，这个方法降低了位移方程的阶数。但是在面面接触算法中，若接触面上含有边界约束条件，形成接触力柔度矩阵时，容易出现矩阵奇异。（2）对角元素充大数法，就是把边界位移为零的那一行对角元素充一个大数，使得非对角元素相对地较小，获得最后求解得到的位移值趋近于零的效果。尽管这种方法较为简便，但取值不当往往会影响计算结果的精度，有时还会使方程变成病态而得不到解；（3）“充0置1”，即将边界位移约束的这一行的对角线元素置1，与这个对角线元素相应行和列的其它元素都充0，位移方程右端的相应行为约束位移值，这样就保证了边界行的位移等于约束值。通过本文反复的数值试验，认为第三种方法的位移约束边界处理方法最适宜本文面面接触模型隐式接触力的求解模式。

面面接触模型的优点可用于任意形状多体接触面，接触面可以具有不同的网格。但这样在接触分析过程中需要进行接触状态判定，以及确定接触点位置。面面接触算法通过全局搜索粗略判断所有可能潜在接触测试对，再由局部搜索找出接触投影点所在单元面的相对位置关系，从而确定接触节点与单元面间的接触状态。本文全局搜索算法融合了主从面算法与位码算法，局部搜索算法继承了点面算法与内外算法的优点。本文研究在现有算法作了以下工作：（1）在全局搜索中构建了描述“接触面对”的主面单元和从面单元的共享实常数，可以将主面单元和从面单元相关联实现快速搜索；（2）在局部搜索中采用了相关单元节点法向“平均向量”，从而解决搜索盲区问题，同时避开求解了点到面投影的非线性方程；（3）在接触力求解方面，采用拉格朗日乘子法的动力方程的增量法，以便解决材料非线性问题；（4）在接触搜索预处理过程中已考虑了接触区域的分解，便于后续的并行程序编制和并行计算；（5）按照所提出的接触算法策略编制了FORTRAN源代码程序。

由本文算法程序得到了计算结果几乎与赫兹接触问题的理论解完全吻合，同时借助于ANSYS商业软件提供的小球算法和拉格朗日乘子法的功能得到的计算数据也与本文算法计算结果几乎完全一致。更重要是本文算法在接触搜索预处理过程中已考虑了接触区域的分解，便于实现后续对高混凝土坝和岩体高边坡静动力稳定分析的并行计算。

致谢：本文研究得到了中国铁道科学研究院刘金朝教授的指导和帮助，北京希格玛仿真技术有限公司完成了程序的调试和测试，作者在此谨表示衷心的感谢！最后，作者要特别感谢匿名评阅人对本文提出的非常中肯且具建设性的修改意见和建议。