沥青混凝土心墙堆石坝地震变形评价方法及其可靠度分析

李炎隆，唐 旺，温立峰，吴海波

（西安理工大学 省部共建西北旱区生态水利国家重点实验室，陕西 西安 710048）

1 研究背景

沥青混凝土心墙堆石坝具有适应变形能力强、防渗性能好、可就地取材、工程造价低等优点，在我国地震频发的西部地区得到了广泛应用［1-3］，然而大坝一旦失事，将会造成不可估量的损失［4］，因此，开展沥青混凝土心墙堆石坝的抗震安全评价研究十分重要。国内外试验结果与实际的地震经历表明，坝体变形破坏是土石坝主要震害形式之一［4-5］。大坝的变形值过大，坝体将会出现明显的不均匀沉降从而产生裂缝，这会直接影响大坝的安全运行［6-7］。因此，考虑坝体的变形，将坝体裂缝作为坝体地震变形破坏的判断依据，来分析土石坝的地震失效概率，是土石坝安全评价的一种新思路。

土石坝地震安全评价一直是工程界最为关注的问题之一，国内外许多学者围绕这个问题开展了研究。赵剑明等［8］从坝坡稳定、地震永久变形以及防渗体安全的角度对高心墙坝进行了极限抗震能力研究。邵磊等［9］基于地震作用下土石坝的变形，提出了高心墙坝极限抗震能力和破坏过程的分析方法，初步建立了大坝抗震极限判别标准。庞锐等［10］基于MSA 法（多条带分析法），对高心墙坝进行了地震易损性分析，研究了适用于高心墙坝地震破坏等级的划分标准。徐斌等［11］将坝顶震陷率和坝坡累积滑移量作为抗震安全评价指标，在不同地震荷载作用下对高心墙坝进行易损性分析。Pang 等［12］采用广义概率密度演化方法，从随机性的角度有效地评价了高土石坝的抗震安全性。吕小龙和迟世春［13］将坝顶震陷率作为地震安全评价指标，考虑了坝体材料属性和地震作用的不确定性，结合蒙特卡罗法提出了高土石坝地震可靠度分析方法。陈玺等［14］提出了洪水及地震共同作用下土石坝坝坡稳定分析方法，为极端工况下坝坡风险分析提供了思路。已有研究成果建立了若干土石坝抗震安全评价指标，并初步用于评价土石坝的地震安全性及失效概率，为土石坝的建设提供了技术支撑。然而，目前将坝体裂缝作为坝体地震变形破坏的判断依据而开展土石坝地震变形失效概率的研究较少。

针对沥青混凝土心墙堆石坝的特点，本文以坝体裂缝作为判断坝体地震变形破坏的依据，将坝体地震变形倾度作为抗震安全控制指标，建立基于倾度法和中心点法的沥青混凝土心墙堆石坝地震变形可靠度分析方法。基于该方法对某沥青混凝土心墙堆石坝实例进行地震变形的可靠度分析，获得该坝设计基准期内的地震变形失效概率。本文研究内容对沥青混凝土心墙堆石坝的抗震设计和地震风险分析有重要的意义。

2 土石坝坝体地震变形评价及其可靠度分析方法

2.1 坝体地震变形评价方法由于坝体材料属性以及坝体可压缩土层厚度的不确定性，地震会促使土石坝坝体不同区域产生不均匀沉降，进而可能导致坝体在竖直方向产生错动。当错动量达到临界状态时，坝体就会沿位移方向形成破坏面。然而坝体在水平方向也会产生位移，这将使得破坏面变成裂缝［15］。目前，倾度法（又称为不均匀沉降斜率法）常被用来进行坝体变形分析［15-17］，该方法能够通过坝体地震变形资料来评价坝体地震变形，具体思路如下：

选取土石坝在同一高程处的两个观测点A、B，如图1所示。假设两点间的水平距离为Δy，A、B处测得的震后沉降量为Sa、Sb，定义震后A′、B′两点间的倾度γ如下［15］：

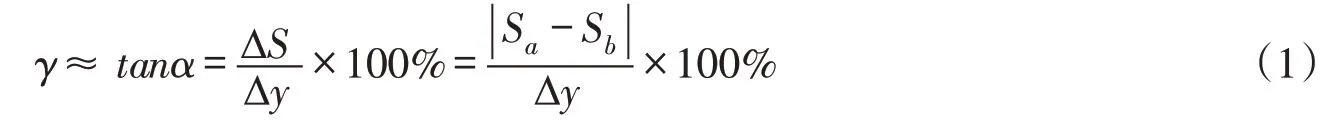
式中：ΔS为Sa、Sb差值的绝对值。

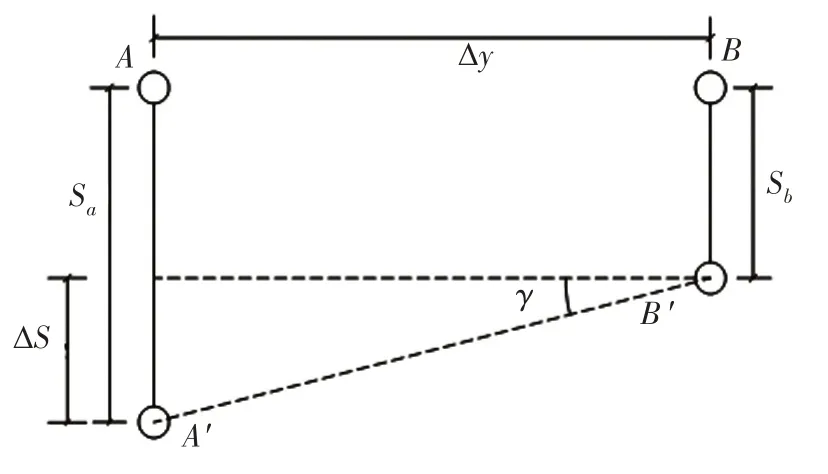
图1 倾度示意图

从式（1）可以看出，倾度法是考虑两点间变形差的问题，其实质是反映水平土层遭受竖直变形差异的程度。假设震后A′、B′两点间临界破坏倾度为γc，则坝体变形破坏状态可以按下式判别：

临界破坏倾度由土料性质、变形条件等多个因素决定。其取值一般可以通过现场测量某一坝段的裂缝来确定，也可以通过土梁挠曲试验获得大坝土料的临界破坏倾度。目前，临界破坏倾度的取值主要通过经验数据确定，李君纯［16］对国内若干产生裂缝的土石坝进行分析，认为临界破坏倾度一般取1%左右是合适的。

2.2 坝体地震变形可靠度分析坝体变形的可靠性可以理解为在一定的外部条件作用下，坝体结构保持稳定的可能性。本文采用中心点法对坝体地震变形的可靠度进行分析，其优点在于可不必知道基本变量的真实概率分布，可以直接用结构功能函数的统计参数表示可靠指标。

假设结构的功能函数为Z：

极限状态可表示为：

其中功能函数的基本变量为Xi=（x1，x2，…，xn），x1，x2，…，xn可以是γc，Δy，ΔS等。在不同时刻不同点，均可获得一组Xi，假设其统计参数中的均值和标准差分别为μxi和σxi。将功能函数Z在中心点M处按照Taylor级数展开，为获得其线性方程，近似地可只取到一次项：

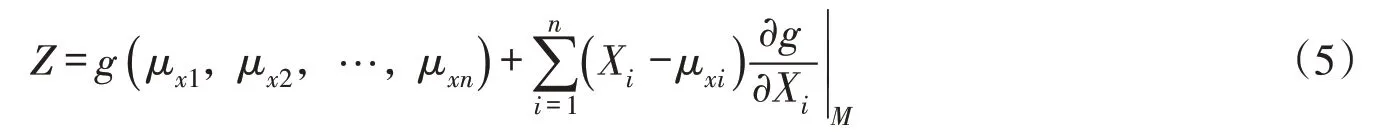
此时，结构功能函数Z的统计参数为：

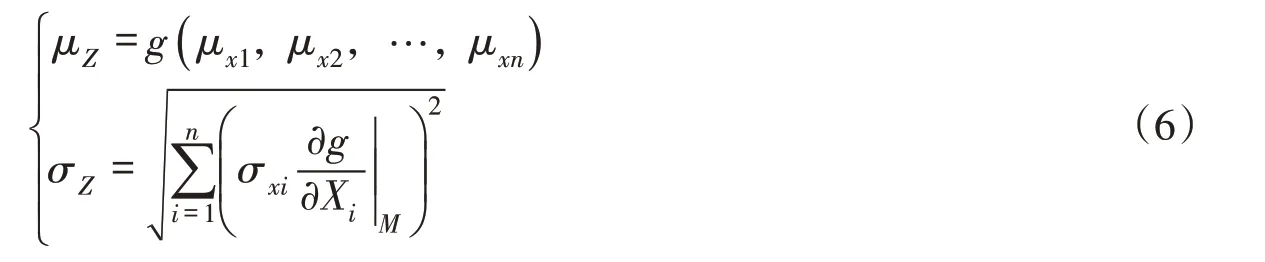
则可靠指标β可表示为：

3 土石坝地震变形失效概率的计算方法

在计算土石坝地震失效概率时，受地震作用不确定性的影响，还应考虑坝址处相应地震烈度的发生概率。地震工程领域中，50年内地震烈度的极大值分布一般符合极值Ⅲ型。因此，t年内地震烈度的概率分布函数可近似地表示为［18-19］：

式中，ω为地震烈度上限值12；I为发生的地震烈度；ε为众值烈度；K为形状参数，可采用分位值法确定，目前由于K的取值方法并不完善，考虑到现行的抗震设计规范，本文采用设计基准期内50年超越概率10%的地震烈度来计算K值［18-19］，后文实例中工程场地50年超越概率10%对应的地震烈度为6.1度，则K=8.612。

坝址处相应地震烈度的发生概率P（I）可用下式表示［20］：

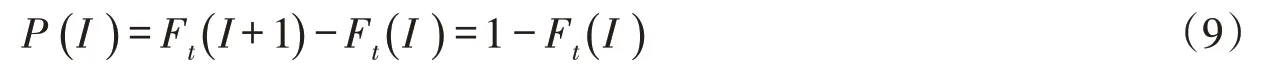
计算出土石坝坝体地震变形可靠指标后，其失效概率pf可根据《水利工程结构可靠性统一设计标准（GB50199-2013）》中“可靠指标与失效概率对照表”查得，也可通过公式Pf=Φ（-β）计算［20］，式中Φ为标准正态分布函数。综上，最终土石坝地震变形失效概率Pf可以通过下式计算：

4 工程实例

4.1 工程概况某沥青混凝土心墙堆石坝最大坝高98 m，坝顶宽度10 m，坝顶高程411 m，坝顶上设有防浪墙，坝轴线全长365 m。大坝坝体与上游围堰结合，坝体上游坝坡高程369.5 m 以上坡比为1∶2.75，以下坡比为1∶2.5。坝体下游坡比为1∶1.8。心墙厚度不等，顶端厚60 cm，横断面呈梯形，在心墙上下游两侧设置360 cm厚的过渡料，底端设置混凝土基座。大坝正常蓄水位为407 m。该坝最大横剖面如图2所示。该大坝属于Ⅱ等大（2）型工程，工程场地50年超越概率10%的基岩水平峰值加速度值为0.55 m/s2，对应地震烈度为6.1 度，100年超越概率2%的基岩水平峰值加速度值为1.29 m/s2，区域构造稳定性好。

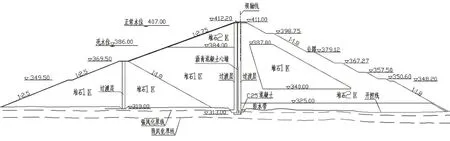
图2 沥青混凝土心墙堆石坝最大横剖面（单位：m）

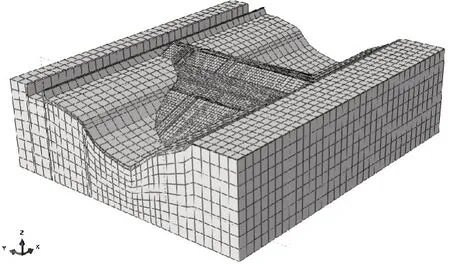
图3 沥青混凝土心墙堆石坝三维计算模型

4.2 计算模型根据该工程的剖面图与平面布置图建立三维有限元计算模型，如图3所示。模型大部分采用六面体八节点单元进行剖分，少数突变处采用四面体四节点单元剖分，模型共计99158 个节点，83854 个单元。模型地基底部设置为全约束，四周设置为法向约束。其中坐标系以顺河向为X轴，向下游为正；以坝轴线方向为Y轴，向左岸为正；以竖直向为Z轴，向上为正。

模型分32个分析步进行模拟，第1步模拟生成地基、岸坡及溢洪道；第2步—第9步模拟围堰分层浇筑至堰顶；第10步模拟堰前蓄水；第11步消除围堰自身位移；第12步—第29步模拟坝体分层浇筑至坝顶；第30步—32步模拟水位由堰前蓄水位升至正常蓄水位。首先进行静力计算，为动力计算提供初始条件；然后将地震产生的动水压力与坝体质量叠加进行动力分析。动水压力采用等效附加质量M0来表示，按式（11）计算［21］。

式中：ρ为水的密度；H0为坝前库水水深；z为计算点水深。

该坝最大坝高为98 m，根据《水工建筑物抗震设计标准（GB51247-2018）》，达到提级标准，按Ⅰ级建筑物设计。提高其设计烈度至7 度，采用100年超越概率为2%的基岩水平峰值加速度1.29 m/s2进行抗震计算。本文采用时程分析法对大坝进行三维动力有限元分析，动力输入采用无质量弹性地基，地震波根据规范（GB51247-2018）给出的标准设计反应谱曲线人工生成，从X、Y和Z三个方向同时输入。计算地震总时长为20 s，时间间隔为0.01 s。三组地震波的时程曲线如图4所示。

4.3 本构模型及计算参数本文静力计算采用在土石坝中应用广泛的邓肯-张E-B 弹性非线性模型［22］，模型中材料参数取值由试验获得，如表1所示。动力计算采用等效线性黏弹性模型［23］，主要参数取值如表2所示。

本文地震永久变形分析采用沈珠江模型和等效节点力法模拟［24］。沈珠江模型中，残余体应变Δεv和残余剪应变Δγs的增量形式表示为：

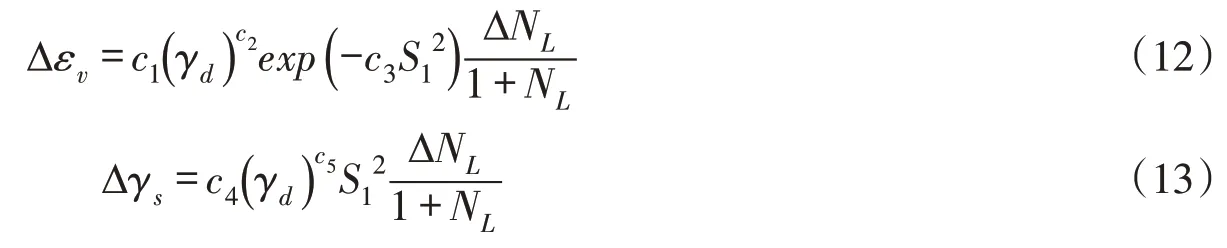
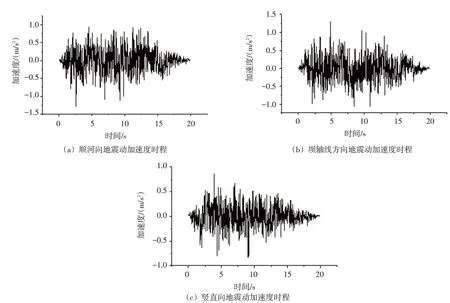
图4 人工合成地震动加速度时程

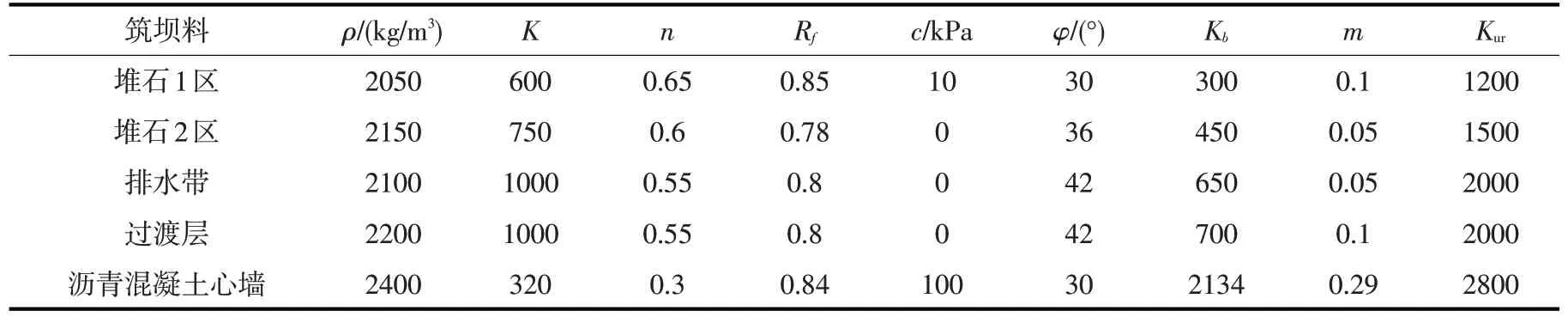
表1 坝体材料静力计算参数

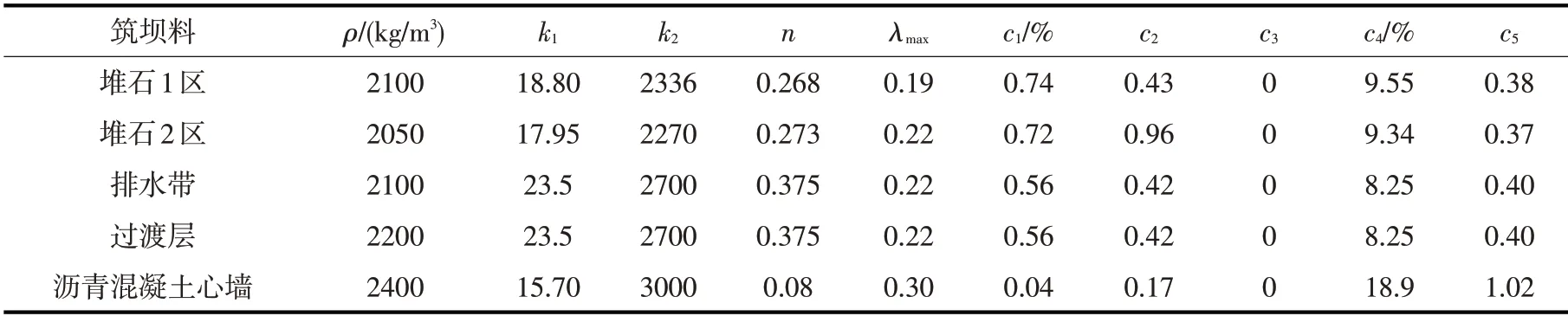
表2 坝体材料动力计算参数及动力残余变形试验参数

式中：NL、ΔNL为振动总次数和时段增量；c1、c2、c3、c4、c5为5 个动力残余变形试验参数，具体取值如表2所示。沥青混凝土心墙堆石坝的动力响应分析不能直接计算出坝体震后残余变形，应将残余应变转换成直角坐标系下的应变，并保证其主轴方向与静力状态的应力主轴方向一致，再把该应变转换为单元的等效静结点力作为外荷载施加于坝体，按静力方法计算坝体残余变形［24］。

4.4 坝体地震变形可靠度分析数值计算模拟实际的施工过程，将坝体整体划分成17 层。为便于分析，本文选取3 个控制断面，分别为坝体最大坝高剖面（坝0+162.71），坝体左岸岸坡剖面（坝0+247.84）以及坝体右岸岸坡剖面（坝0+110.77）进行分析。根据4.3 节的计算方法对该坝进行永久变形计算，然后通过倾度法和中心点法对该坝进行坝体地震变形可靠度分析。由于该坝为心墙坝，每层土层需要从心墙上、下游两侧分别进行分析。在同一侧同一土层中，选取多组连续结点A、B，尽量保证每组结点的水平距离Δy一致。本文选取的结点即为模型有限元网格上的结点，在对模型进行网格剖分时，尽量使同一水平上的网格结点间距一致。根据每组结点的水平距离Δy和A、B结点的沉降量Sa、Sb，基于式（1）计算出每组的倾度。然后根据中心点法，得到该土层的坝体地震变形可靠指标。坝体地震变形倾度计算示意图，如图5所示。其它土层以同样的方法进行坝体地震变形可靠指标计算，各土层变形可靠度指标计算结果如表3所示。

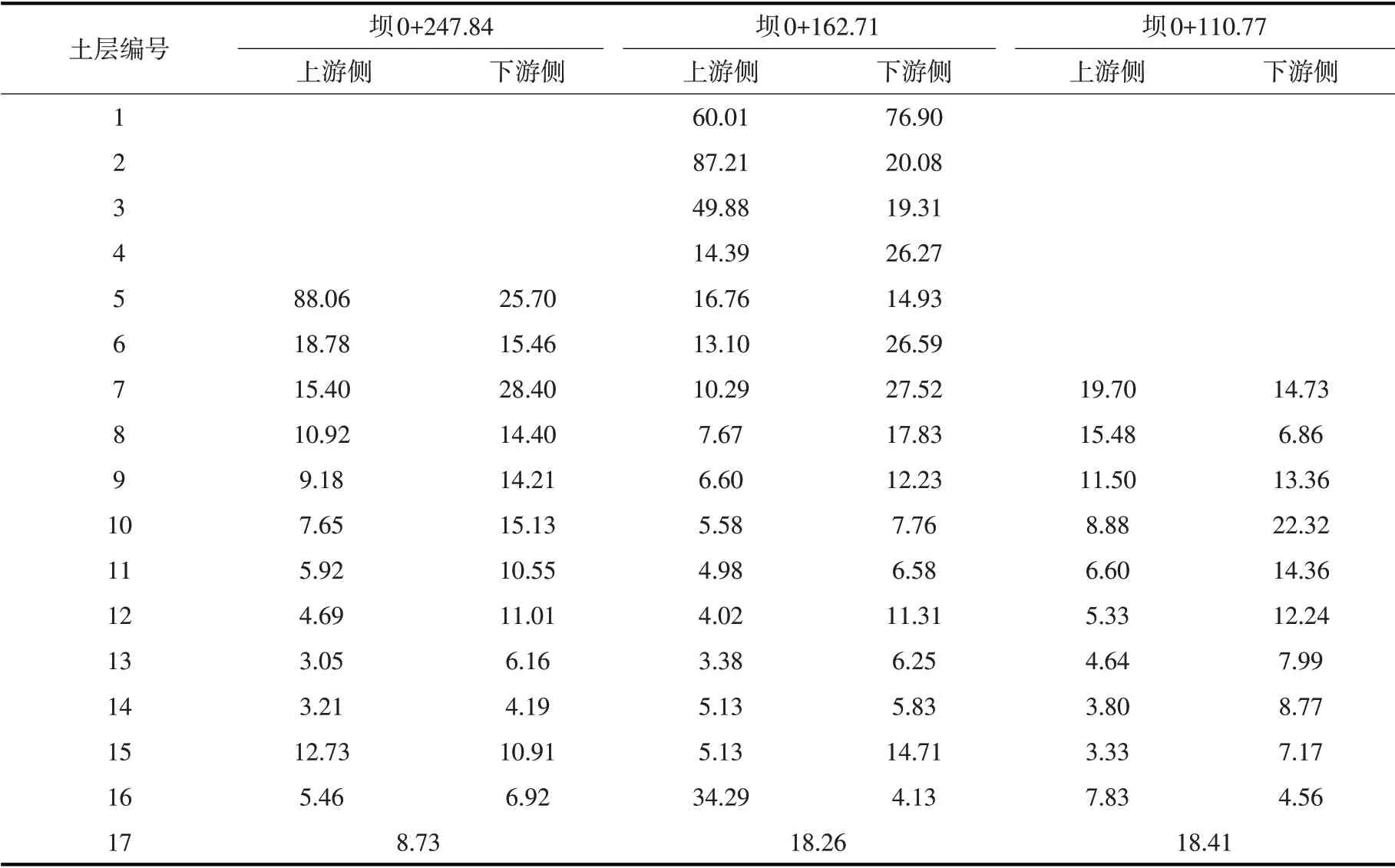
表3 某沥青混凝土心墙堆石坝坝体地震变形可靠指标计算结果

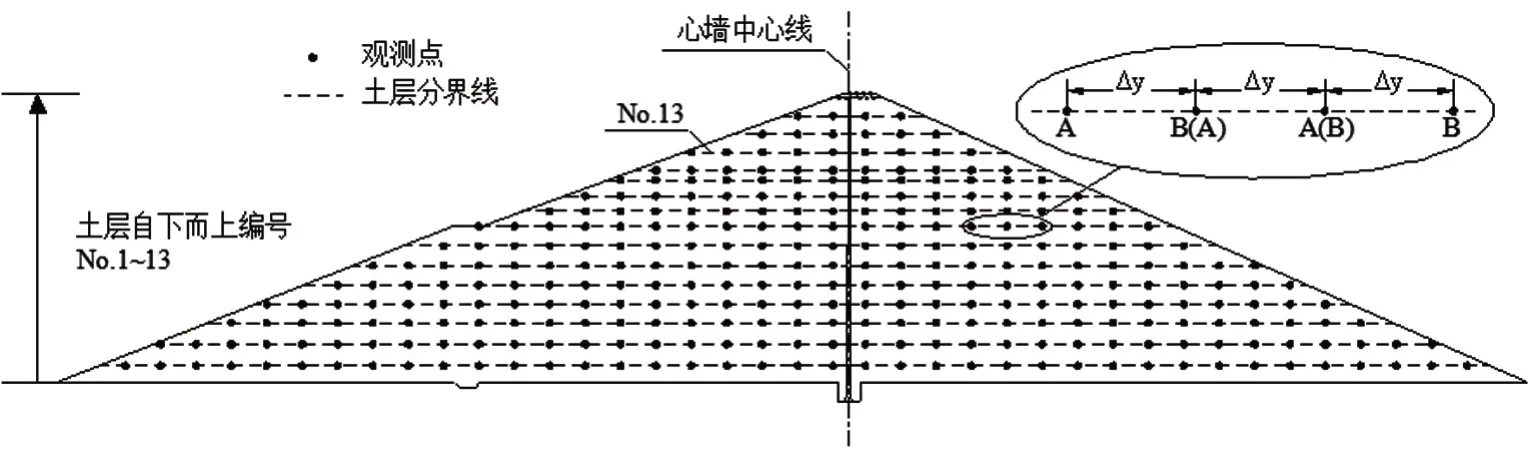
图5 坝体变形倾度计算示意图

由表3可知：坝体地震变形可靠指标的最小值为3.05，说明此处失效风险最大。由图2、图5可以看出，最小可靠度指标位置位于坝体左岸岸坡剖面（坝0+247.84）上游侧第13 号土层靠近坝顶及筑坝材料堆石1、2 区分界的位置。受不同材料差异的影响，该处变形（竖直与水平）相对坝体其他区域较大，容易产生坝体变形破坏，影响大坝安全。最终该坝坝体地震变形的可靠指标为3.05。

4.5 地震变形失效概率计算在水利工程规范中，以年计失效概率推导的允许可靠指标，作为结构承载能力控制标准被广泛接受。陈祖煜［25］建议，由于大部分的岩土工程建造年代久远，其工程寿命应比设计基准年大，可以假定工程寿命T等于其设计基准年Nd，则年计失效概率Py可表示为：

由4.4节分析可知，实例的坝体地震变形可靠指标为β=3.05，其失效概率可通过公式Pf=Φ（-β）或者规范（GB50199-2013）中“可靠指标与失效概率对照表”获得；根据规范（GB50199-2013）规定，I级主要建筑的设计寿命为100年，则坝址处发生该坝基本设计烈度地震的概率P（I）可由式（9）计算；进而地震变形失效概率Pf可根据式（10）计算；最终该坝设计基准期内的年计地震变形失效概率Py可根据式（14）计算，计算结果如表4所示。

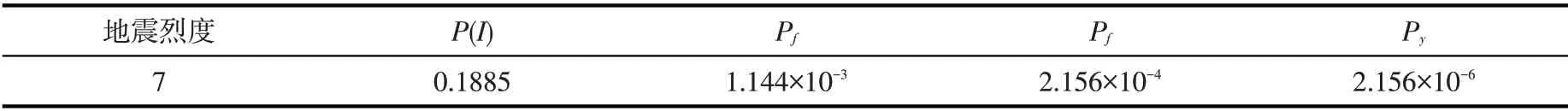
表4 沥青混凝土心墙堆石坝的地震变形失效概率

结构稳定的可靠性应以可靠指标表示，可按公式β=Φ-1（1-Py）计算设计基准期内的地震变形可靠指标，式中Φ-1为标准正态分布的反函数，根据上式获得该坝地震变形可靠指标β=4.6。规范（GB50199-2013）规定可靠指标应满足β≥βt，βt为结构承载力极限状态的目标可靠指标，如表5所示。从表5可以看出本文计算得到的实例可靠指标4.6大于I级水工建筑物一、二类破坏的目标可靠指标3.7和4.2。此外，规范（GB50199-2013）也规定偶然状况的目标可靠指标可低于设计状况的目标可靠指标。根据以上分析可知，从坝体地震裂缝的角度考虑，该坝基本满足规范的设计要求，工程偏于安全。

表5 结构持久设计状况承载能力极限状态的目标可靠指标βt

5 结论

本文以坝体出现裂缝作为判断坝体变形破坏的依据，将坝体地震变形倾度作为地震安全控制指标，建立了基于中心点法和倾度法的沥青混凝土心墙堆石坝地震可靠度分析方法。该方法可同时考虑坝体材料的复杂因素和地震作用的不确定性。通过对98 m 高的某沥青混凝土心墙堆石坝进行分析，验证了该方法的可行性，结果表明：

结合中心点法和倾度法计算地震变形可靠度指标，不仅可以考虑坝体材料分区的影响，而且在计算可靠指标时可不必知道基本变量的真实概率分布。此外，坝体地震变形等数据较容易在地震记录中获取。因此本文的可靠度分析方法简单易行，便于实际工程应用。

某沥青混凝土心墙堆石坝在上游侧靠近坝顶处的地震变形失效风险最大。基于本文提出的土石坝地震变形可靠度分析方法，计算获得某沥青混凝土心墙堆石坝设计基准期内的年计地震变形失效概率Py=2.156×10-6，对应的可靠指标β=4.6，满足规范的设计要求，说明坝体整体结构稳定。

地震作用下沥青混凝土心墙堆石坝还有坝坡失稳、渗漏破坏、砂土液化、心墙破坏等震害形式，单一的评价指标很难准确地进行地震风险评价。因此，后续研究中有必要考虑更多的评价指标，进一步完善沥青混凝土心墙堆石坝地震可靠度分析方法，为沥青混凝土心墙堆石坝的抗震设计、地震风险分析以及风险等级的建立提供依据。