高考数学能力小题训练(4)
一、填空题
2.已知z+2z-=9+4i(i为虚数单位),则|z|=
4.在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如右面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90~120km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有辆.
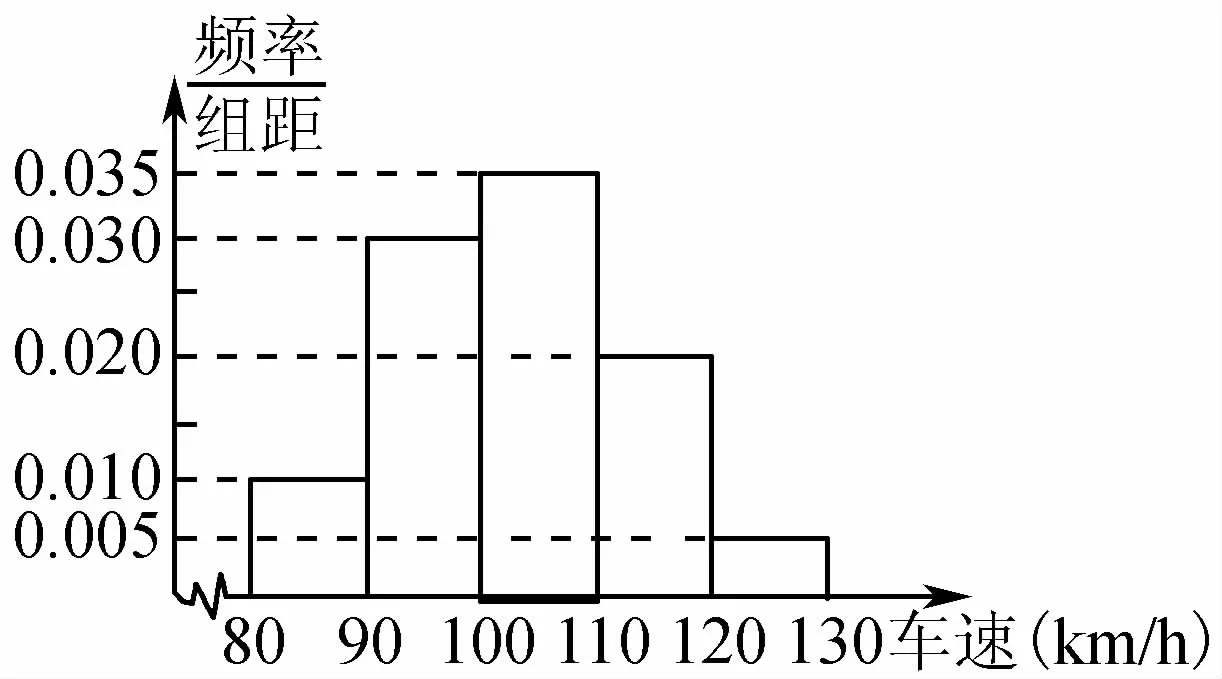
(第4题)
5.已知m,n表示两条不同的直线,α,β表示两个不同的平面,且m⊂α,n⊂β,给出以下匹个命题:
①若α∥β,则m∥n;
②若m⊥β,则α⊥β;
③若m∥β,则α∥β;
④若α⊥β,则m⊥n.
构建以职业能力培养为核心的三级项目课程体系,让企业项目引领课程教学。课程体系以三种级别的企业实际工程项目为载体,规划与整合专业课程资源,以“做项目”为主线,分阶段对学生的知识、能力和素养进行培养。其中1级项目体现专业综合知识与能力,涵盖整个教学阶段的主要课程;2级项目体现某个阶段综合知识与能力,涵盖该阶段的主要课程;3级项目主要体现某门课程基本知识与能力。在此课程体系中,以1级项目为主线的三种级别项目共同将整个专业的主要课程连成一体,通过对学生系统地进行构思、设计、实现和运作的整体项目训练,培养学生的职业能力与素养。
6.已知函数f(x)的部分对应值如下表所示.数列{an}满足a1=1,且对任意n∈N*,点(an,an+1)都在函数f(x)的图象上,则a2017的值为

x 1 2 3 4 f(x) 3 1 2 4
7.“a>1”是“函数f(x)=ax+cosx在R上单调递增”的条件.(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)
8.(2020年淮安联考)在正方形ABCD中,M,N 分别是BC,CD 的中点,若,则实数
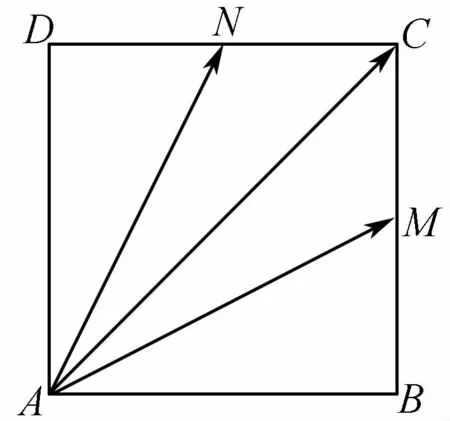
(第8题)
9.在锐角三角形ABC中,a,b,c分别是角A,B,C 的对边,已知a,b是方程x2-的两个根,且
11.在平面直角坐标系中,给出点A(1,0),B(4,0),若直线x+my-1=0上存在点P,使得|PA|=2|PB|,则实数m 的取值范围是
12.已知函数f(x)=|x2-3x|,x∈R.若方程f(x)-a|x+1|=0恰有4个互异的实数根,则实数a的取值范围是
13.在△ABC 中,AB=AC,D 为线段AC 的中点,若BD 的长为定值l,则△ABC面积的最大值为.(用l表示)
14.设a,b∈Z,若对任意x≤0,都有(ax+2)(x2+2b)≤0,则a+b=
二、解4题
(1)求α的值;
(2)求f(x)的最小正周期和单调递减区间.

16.已知圆O:x+y=1的切线l与椭圆C:x2+3y2=4相交于A,B 两点.
(1)求椭圆C的离心率;
(2)求证:OA⊥OB;
(3)求△OAB 面积的最大值.


