教你读懂数学建模问题——高考中的概率分布试题例析

祝维男

说起概率分布的应用，同学们很快就联想到我们的生活实际、科学技术等，它也成为了高考命题中数学模型的重要载体.下面一起来看看近几年高考中概率分布的典型问题，探究分析模型特点，总结命题规律，从而提升数学建模能力.

1．源自生活实际的精细模型

例1 （2017 年全国Ⅲ卷第18 题）某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4 元，售价每瓶6 元，未售出的酸奶降价处理，以每瓶2 元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500 瓶；如果最高气温位于区间[20 25， )，需求量为300 瓶；如果最高气温低于20，需求量为200 瓶，为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得右面的频数分布表：

最高气温[10,15) [15,20) [20,25) [25,30) [30,35) [35,40)天数 2 16 36 25 7 4

以最高气温位于各区间的频率代替最高气温位于该区间的概率．

（1）求六月份这种酸奶一天的需求量X（单位：瓶）的分布列；

（2）设六月份一天销售这种酸奶的利润为Y（单位：元）．当六月份这种酸奶一天的进货量n（单位：瓶）为多少时，Y 的数学期望达到最大值？

分析 （1）根据题意，列出六月份这种酸奶一天的需求量X 的可能取值，计算出得分X 所对应的概率值，写出X 的分布列为；

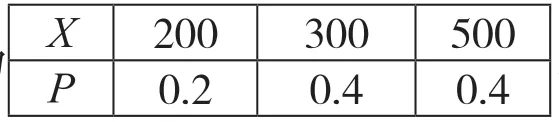
X 200 300 500 P 0.2 0.4 0.4

模型解读

日常生活中的“酸奶销售”大家都很熟悉，模型中的关键条件是“酸奶的不同标价”和“气温变化对酸奶需求量的影响”．解题时要围绕进货量n进行分类讨论．

2．源自科学技术的精细模型

例2 （2019 年全国Ⅰ卷理科第21 题）为了治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验．试验方案如下：每一轮选取两只白鼠对药效进行对比试验．对于两只白鼠，随机选一只施以甲药，另一只施以乙药．一轮的治疗结果得出后，再安排下一轮试验．当其中一种药治愈的白鼠比另一种药治愈的白鼠多4 只时，就停止试验，并认为治愈只数多的药更有效．为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1 分，乙药得−1分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1 分，甲药得−1分；若都治愈或都未治愈则两种药均得0 分．甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X．

（1）求X 的分布列；

（2） 若 甲 药、 乙 药 在 试 验 开 始 时 都 赋 予4 分，

表示“甲药的累计得分为i 时，最终认为甲药比乙药更有效”的概率，则其中a P X= =−( 1)，b P X= =( 0)，c P X= =( 1).假设α =0.5，β =0.8．

（i i）求p4，并根据p4的值解释这种试验方案的合理性．

模型解读

你是不是觉得自己在做阅读理解题，读完一遍不知道题目说的是啥？那就对了，就是为了考验你们的阅读理解能力和耐力!本题以药物的试验为模型：第一部分详细介绍了药物试验的实施方案，第二部分是将试验实施方案抽象成数学问题的再描述，第三部分经过层层提问，促进对模型内部关系的理解．

分析 （1）结合题目条件写出X 所有可能的取值，计算出得分X 所对应的概率值，写出X 的分布列为

?

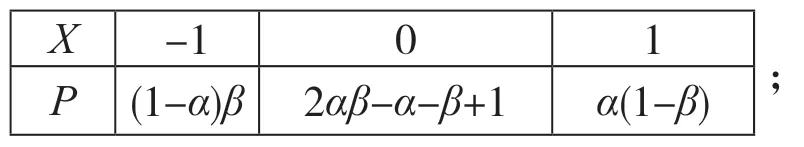
（2）（i） 将α， β 代 入（1） 中 得a b c, , 的 值， 所 以变形后结合等比数列的定义得证；（ii）求出等比数列的通项公式，根据p8和p0的值，采用迭加的方法求得p1；继续利用迭加的方法可求出p4为.

3. 源自组合数学的精细模型

例3 （2019 年江苏卷第23 题）在平面直角坐标系xOy 中，设点集An=从集合Mn中任取两个不同的点，用随机变量X表示它们之间的距离．

（1）当n=1 时，求X 的概率分布；

分析

（1）当n=1 时，M1中的点的分布如图1 所示;首先确定随机变量X 可能的取值，然

后计算出相应的概率值即可确定分布列为

X 1 2 2 5 P 7 2 4 2 ；15 15 15 15

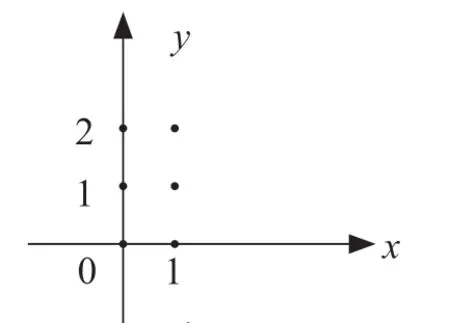
图1

（2）为避繁就简，可以考虑对立事件的问题先求解 P X n( > )的值，设A（a,b）和B c d( )， 是从Mn中取出的两个点，由条件中的点集，分b d= ；b=0，d =1；b=0，d =2；b d= =1, 2 四种情况确定满足X n> 的X 所有可能的取值，再求解相应的概率值得结果.

模型解读

【归纳提升】

以上几类模型的概率分布试题，背景新颖，乍看往往不知道如何下手.因此同学们要注意培养阅读理解能力以及提出问题、获取信息、处理数据的能力.

小试牛刀

“学习强国”APP 包含文章学习和视频学习两类，且这两类学习互不影响．已知积分规则如下：每阅读一篇文章积1 分，每日上限积5 分；观看视频累计3 分钟积2 分，每日上限积6分．经过抽样统计发现，文章学习积分的概率分布表如表1 所示，视频学习积分的概率分布表如表2 所示．

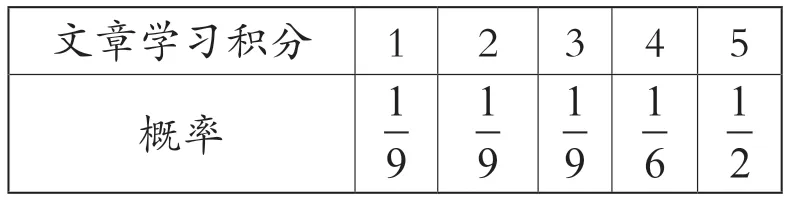
表1

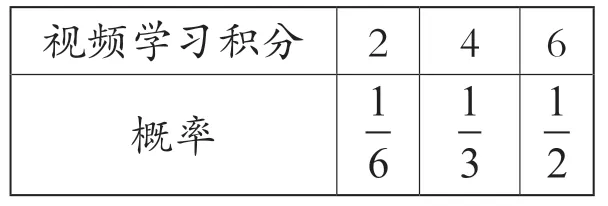
表2

（1）现随机抽取1 人了解学习情况，求其每日学习积分不低于9 分的概率；

（2）现随机抽取3 人了解学习情况，设积分不低于9 分的人数为X，求X 的概率分布及数学期望．