贝叶斯判别中对样品判别的评价研究

张国俭

（晋中学院数学学院，山西晋中 030619）

贝叶斯统计是统计学的一个重要的学派，它应用了先验信息、样本信息、总体信息3种信息。而经典统计只应用了样本信息和总体信息，所以，只要先验分布选取合理，会得到比经典统计学更精确的结果[1-3]。

贝叶斯判别分析是贝叶斯统计在判别分析中的应用[4]，在总体是正态分布的情况下，它的判别函数可以看成马氏距离判别函数的推广，特别是协方差矩阵相等的情况下。

贝叶斯判别虽然可以由后验概率来看样品判别的优劣，但对于两个总体的后验概率相等或很接近的情况，判别便没有了实际意义。对协方差矩阵相等的正态总体，在误判损失相等情况下的贝叶斯判别进行了研究，提出了待判域的概念，用以鉴别误判损失没有统计学意义的样品；提出了判别系数的概念，用以对样品判别的优劣进行评价。

1 准备知识

定理1设G1和G2是两个不同的p维正态总体，先验分布分别为p1和p2，均值向量分别为μ1和μ2，协方差矩阵相等且都为Σ，x0为一样品值，记c(i|j)，i,j=1,2表示把属于Gj的样品误判为Gi造成的损失，当则判别准则为：

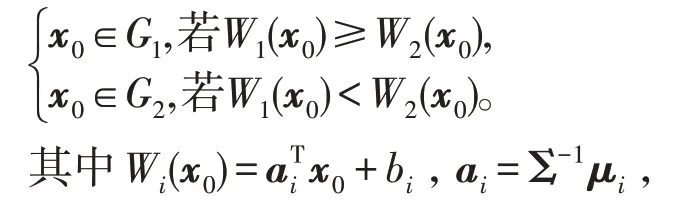
定理2设G1,G2,…,Gk是k个不同的p维正态总体，其先验分布为p1,p2,…,pk，均值向量分别为μ1,μ2,…,μk，协方差矩阵相等且都为Σ，x0为一样品值，记c(i|j)，i,j=1,2,…,k表示把属于Gj的样品误判为Gi造成的损失，当则判别准则为

定理3设G1,G2,…,Gk是k个不同的p维正态总体，其先验分布分别为p1,p2,…,pk，协方差矩阵相等，且都为Σ，

则后验概率为：

对于x是p维随机向量，有如下的结论：

定理4设x～Np(μ,Σ)，又Y=ATx+b，其中b为p维常向量，AT是l×p矩阵，rank(AT)=l，则Y～Nl(ATμ+b,ATΣA)[1]。

设x1,x2,…,xk是属于k个不同的p维正态总体的随机向量且相互独立，记ci=P(Gi|x),i=1,2,…,k,则任一待判样品是合理的。

定理5设xi～N(μi,Σ)，x=，i=1,2,…,k,ci为已知常数，则

证明显然随机变量x服从正态分布,求x的数学期望与方差：

因为x1,x2,…,xk相互独立，所以

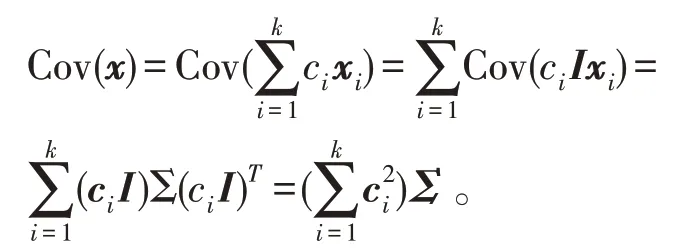
其中I为p×p单位矩阵，

证毕。

定理6记，x～N(μ,c2Σ)，则

证明x是来自p维正态总体的任一样品，由定理4知，随机变量Wi(x)服从正态分布。求Wi(x)的数学期望与方差：

证毕。

定理7若x～N(μ,c2Σ)，记Wij(x)=Wi(x)-Wj(x)，i,j=1,2,…,k且i≠j，则

证明设

由x～N(μ,c2Σ) 及定理4知，W(x) 服从正态分布。

证毕。

2 显著性检验

贝叶斯判别可以用误判概率或误判损失来刻画判别的优劣，但这只是对判别标准的评价，对样品可以用后验概率来进行评价。但如果样品属于两个总体的后验概率相等时，就无法对其进行判别，即使把其归为其中的一类，其判别的实际意义也不大。同理，如果样品属于两个总体的后验概率虽然不等，但很接近，其实际意义也不大。故有必要对其进行显著性检验。

对样品的判别函数的差异进行显著性检验。提出了待判域的概念，用以对数据指标没有明显所属的样品进行鉴别；提出了判别系数的概念，用以对样品的判别优劣进行评价。

对一个固定的样品来说，不同的观测有不同的观测向量，故可以把它看作一个随机向量。设样品x=(x1,x2,…,xp)T是p维空间中的一个随机向量，由1的讨论知，x～N(μ,c2Σ) 而具体的数据向量x0=(x10,x20,…,xp0)T看成x的一个观测向量，对判别函数的差异做显著性假设检验。

2.1 两个正态总体的情形

设G1和G2是两个不同的p维正态总体，其先验分布为p1和p2，其均值向量分别为μ1和μ2，协方差矩阵相等且都为Σ。当由定理1知，可以确定判别函数Wi(x),i=1,2。

不妨设W1(x0)>W2(x0)，对E(W1(x))>E(W2(x))做显著性检验：

提出假设

等价于(a1-a2)Tμ+(b1-b2)>0。

记d=(a1-a2)Tμ+(b1-b2)，

则假设等价为

由定理7知

故取检验统计量为

拒绝域{u≥u1-α}[5]，其中u1-α为标准正态分布的下侧1-α分位数。

{u≥u1-α}等价于W12(x)≥

定义1把上面的保留域{u

由定义1知道，如果x0落入待判域，说明判样品x0到两个总体的损失的差没有统计学意义。可以把x0作为待观察的对象。

检验的p值为：p=1-Φ(u0)，其中u0是由x0算出的u值。

由p值的意思可知，p值越小，越拒绝原假设，判别越好。

定义2把R=1-p=Φ(u0)称为样品x0的判别系数。

由定义2知道，0

2.2 k 个不同的p 维正态总体的情形

设G1,G2,…,Gk是k个不同的p维正态总体，其先验分布分别为p1,p2,…,pk，均值向量分别为μ1,μ2,…,μk，协方差矩阵相等且都为Σ，当时，由定理2知，判别准则为

在这种情形下，对算出来的Wi(x0),i=1,2,…,k，进行从大到小排序，只取前两个，分别记为W(1)(x0),W(2)(x0)，不妨设W(1)(x0)>W(2)(x0)。

类似两个正态总体，对E(W(1)(x))>E(W(2)(x))做显著性检验。

假设为

由定理5知

拒绝域{u′≥u1-α}。

若{u′W(2)(x0)没有统计学意义，说明判x0属于总体（1）和判x0属于总体（2）的损失没有统计学差别，x0可以被判属于总体（1），也可以被判属于总体（2），甚至还可以被判属于其他总体。这时，x0是待判的。即待判域为{u′

否则，W(1)(x0)>W(2)(x0)判x0属于不同总体的损失有统计学意义。就可以说，x0到（1）这个总体的损失最小。判x属于总体（1）。

判别系数为：R=，其中，是由x0算出的u′值。

3 不足及需要改进的地方

（1）只研究了协方差阵相等的正态总体的情形，并且误判损失相等的情形，其他情形没有研究；

（2）对样品的评价除了待判域和判别系数外还应该考虑判别函数整体的评价，最好做个综合指标；

（3）没有做实证研究，还需要做实证以检验判别的误判率的改进程度。