一类病毒自发变异时滞SIR传染病模型稳定性分析
李冬梅 付玉立 高添奇 李晨辰
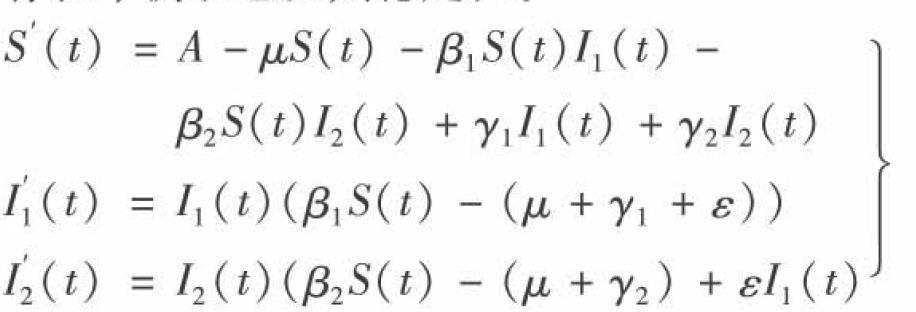
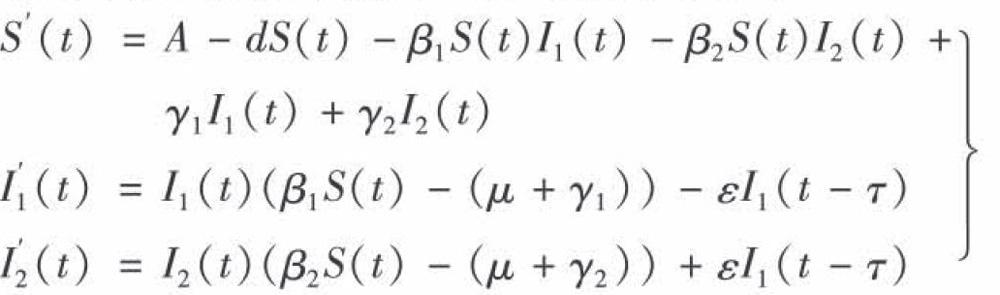
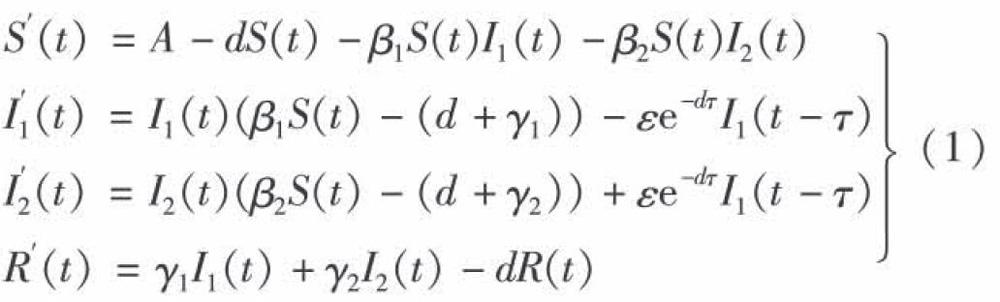
摘要:考虑了病毒自发变异对传染病流行的影响,建立了具有自发病毒变异的时滞SIR传染病模型,给出无病平衡点,单株地方病平衡点和地方病平衡点的存在性、局部稳定充分条件。通过构造Liapunov函数,证明了无病平衡点、单株地方病平衡点和地方病平衡点全局渐近稳定性。借助数值模拟的方法,分析了病毒自发变异对疾病传播的影响。
关键词:病毒自发变异;平衡点;稳定性
DOI:10.15938/j.jhust.2020.02.022
中图分类号:0175.1文献标志码:A 文章编号:1007-2683(2020)02-0166-07
0引言
传染病动力学模型在了解疾病的传播规律和预测疾病流行趋势中发挥着极其特殊的作用。针对病原体为病毒类型的传染病,可借助病毒动力学传染病模型的定量分析来了解疾病的变化趋势,制定疾病防控策略已取得诸多的结果。但是,病毒在其传播过程中受到多因素的影响,可能会发生自身变异现象,从而改变原有的传播规律和治愈率,病毒变异感染者会再次传播疾病可能会导致疾病流行。无变异病毒动力学模型的研究结果无法了解更多的病毒变异后疾病流行趋势,如乙肝病毒、狂犬病毒。通过研究带有病毒变异后的传染病模型,将有助于了解疾病感染者数量的最终演变趋势,可为制定防控措施提供一定理论依据。有关病毒变异传染病传播问题的研究结果不多。文考虑病毒感染者和病毒变异感染者两类人群均具有传染性,经过治愈后不具有免疫性,建立了如下分段传播的无免疫一类的传染病S赐模型,研究了两类人群存在平衡状态及其稳定性。
文考虑病毒变异感染者是由病毒感染者经过一定时间时滞转移而来的,建立了如下无免疫的一类具有时滞的病毒变异的5/s模型,研究了模型的无病平衡点和地方病的稳定性。
本文考虑了病毒侵人感染者体内经过治疗,部分感染者治愈而获得免疫。还有部分感染者会在一段时间内发生病毒变异,成为新的一类感染者,这类人群可以采取新的治疗措施,治愈后也获得免疫。在此治疗期间这两类患者均具有感染能力。因而建立了如下带有双线性发生率的具有免疫的病毒自身变异的时滞传染病SIX模型。
其中S(t),I1(t),I2(t),R(t)分别是t时刻易感人数、病毒自身变异前的患者、病毒自身变异后的患者和恢复的人数;A是输入率;β1和β2分别表示病毒自身变异前患者和病毒自身变异后患者的传染率系数;ε为变异前患者变为变异后患者的速率;d为死亡率;γ1为病毒自身变异前的恢复率;γ2为病毒自身变异后的恢复率;τ为病毒自身变异时间。假设ε
显然区域Ω={(S,I1,I2)|S(t)≥0,I1(t)≥0,I2(t)≥0,S(t)+I1(t)+I2(t)≤A/d|是模型(2)正向不變集。
1 主要结果
1.1 模型平衡点的局部稳定性
模型(2)的平衡点满足下列方程
2 数值模拟
取模型(1)中的参数A=10,d=1,β1=0.03,β2=0.05,ε=0.1,τ=0.01,γ1=0.02,γ2=0.04.经计算满足R2≤R1≤1,定理3可知无病平衡点E0全局渐近稳定,其数值模拟图见图1.
若取模型(1)的参数为A=10,d=0.4,ε=0.03,τ=0.1,β1=0.02,β2=0.04,变异前的恢复率γ1,变异后的恢复率γ2分别取γ1=0.02,γ2=0.4;γ1=0.2,γ2=0.5.
经计算,均满足R1<1,R2>1,由定理4,知单株地方病平衡点是全局渐近稳定的,其数值模拟图见图2(a),2(b)。
取模型(1)中的参数为A=8,d=0.4,β1=0.03,β2=0.05,ε=0.09,τ=0.1,变异前的恢复率γ1变异后的恢复率γ2分别取γ1=0.02,γ2=0.4;γ1=0.02,γ2=0.5;γ1=0.1,γ2=0.4,经计算均满足R2<1,R1>1,由定理6,模型(1)存在地方病平衡点E2全局渐近稳定,其数值模拟图见图3(a),图3(b),图3(c),图3(d)。
若取模型(1)中的参数为A=10,d=0.4,ε=0.03,τ=0.1,β1=0.05,β2=0.03,变异前的恢复率γ1变异后的恢复率γ2分别取γ1=0.2,γ2=0.5;γ1=0.3,γ2=0.2.经计算,满足R1>R2>1,由定理1知,模型(1)存在单株地方病平衡点E1,地方病平衡点E2。模型(1)的数值模拟图如图4(a),4(b)所示。发现地方病平衡点是稳定的,单株地方病平衡点是不稳定的。

