基于改进Census变换和网状聚合的立体匹配方法
刘爽 陈德运


摘要:为了获得连续稠密的视差图像,提出了一种基于改进Census变换和网状代价聚合的立体匹配方法。在初始匹配代价计算中,用灰度排序剔除极值的方法获取参考像素,改善Census变换对于亮度差异的抑制效果。在代价聚合计算中,采用SLIC超像素分割方法对图像进行区域划分,在区域内按照网状搜索去寻找邻域像素,并根据邻域像素距离待匹配像素的远近配置权重,完成待匹配像素的代价聚合。实验结果表明,提出算法计算出的视差图像,坏像素比例低、视差连续而稠密,其性能与Middlebury平台上排名第一的Locamxp算法接近。
关键词:稠密视差图像;立体匹配;Census变换;网状聚合
DOI:10.15938/j.jhust.2020.02.004
中图分类号:TP391文献标志码:A 文章编号:1007-2683(2020)02-0025-06
0 引言
Daniel将稠密视差图像的计算方法划分成四个阶段,初始匹配代价计算、代价聚合、视差计算、视差优化。其中,初始匹配代价求取的准确性、代价聚合的可靠性,对于整个立体匹配方法具有决定性影响。
起初,初始匹配代价计算广泛采用了像素灰度相似性作为是否匹配的判断依据。但是像素灰度对于光照因素过于敏感,导致光照不均匀时匹配代价计算不准确。为此,Hirshmuller提出了运用Cen。SUS变换算子计算初始匹配代价的思路。Census变换算子确实具有明显的光照鲁棒性,但过于依赖于变换区域中心像素的准确性。因此,只有保障中心像素信息的准确性,才能保证初始匹配代价计算的准确性。
对于局部匹配算法而言,代价聚合是提升整个算法匹配精度的最重要手段。在代价聚合的研究工作中,最早出现的是矩形窗口。但矩形窗口的形状是固定的,在图像上的漫游过程中也容易将噪声像素纳入聚合体系,从而导致代价聚合结果的不准确。为此,Zhang提出了一种十字形交叉聚合窗口,并根据其它像素和中心像素的颜色相关性、空间距离相关性,灵活地调整调整窗口的大小,以尽可能剔除聚合窗口中的噪声干扰。Cheng根据各像素初始匹配代价的关联性,构建了一个交叉树状的聚合结构,这个交叉树由水平树和垂直树构成,进而结合区域边缘约束实现了更加准确的匹配。Li将最小生成树方法和3D标签技术结合起来,设计了一种3D代价最小树随机搜索策略,实现了快速而有效的代价聚合。
本文在Middlebury框架的基础上,在初始匹配代价计算和代价聚合阶段提出新的方案,构建出一种新的立体匹配方法以获得更加理想的稠密视差图像。
1 提出的立体匹配方法
1.1 改进Census变换计算初始匹配代价
以像素灰度作为依据来计算匹配代价,对于光照条件非常敏感。如果立体视觉传感器中两个像机接收的光强不一致,就容易形成立体图像对中左右两个图像的亮度差异较大,导致匹配代价计算出现较大误差。因此,本文选择了对光照条件更为鲁棒的Census变换方法,来完成初始匹配代价的计算。但是Census变换对参考像素比较敏感,如果参考像素受到了噪声污染,就容易导致匹配代价计算的不准确。为此,本文建立一个新的流程来确定参考像素,以提升其对噪声的敏感性。
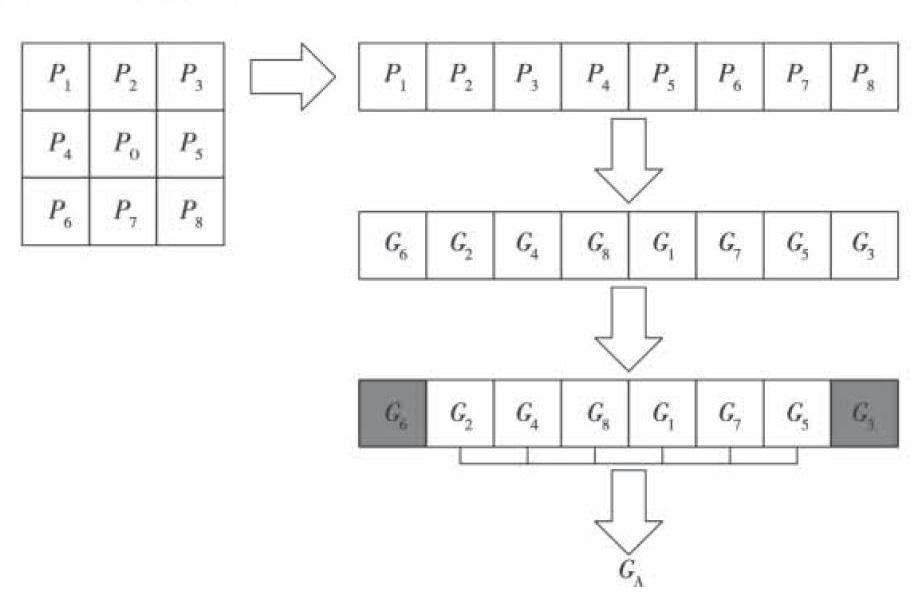
以一个3*3的窗口为例,参考像素值确定的方法如图1所示。
图1中,P0]为要计算初始匹配代价的像素,Pi(i=1,2,…,8)为像素P0的邻域像素。首先,按照像素位置将8个邻域像素进行排列。其次,根据像素灰度值的大小调整8个像素的位置关系。再次,去掉8个像素中的灰度值最小像素和灰度值最大像素。最后,以剩余6个像素的灰度平均值作为参考像素的灰度值。
接下来,按照Census变换方法的流程,计算Po的初始匹配代价。
计算变换窗口内的比特串,处理如下:
式中:B(P0)为以P0为待处理像素计算出的Bit串,GA对应于图2中的参考像素灰度;Pi代表像素P0的邻域像素;C(只)代表邻域像素的灰度;×表示按位连接的操作。
按照式(1)的方法,分别计算立体图像对中左右图像对应的Bit串,可得BL(P0)、BR(P0)。BL(P0)表示左图像的Bit串,BR(P0)表示右图像的Bit串。进而在搜索视差范围的约束下,可以计算出像素P0的初始匹配代价,如下:
C(Po,d)=Hamming[BL(Po),BR(P0+d)] (2)式中:d為搜索视差;Hamming[·]为汉明距离;C(P0,d)为像素P0的初始匹配代价。
1.2 基于网状搜索的代价聚合
代价聚合,是将待匹配像素及其周围邻域像素的初始匹配代价进行聚合,以增强待匹配像素匹配代价的可信度。在立体匹配算法发展的早期阶段,固定大小的矩形窗口是普遍使用的聚合窗口。但是,矩形窗口内的邻域像素,有的可能和带匹配像素缺乏局部灰度、局部纹理的相关性。这些像素的初始匹配代价,对于待匹配像素匹配代价可信度的提升具有严重的负面影响。因此,学者们提出了不同的聚合窗口以提升邻域像素和待匹配像素之间的关联程度。
本文中,采用超像素分割方法对图像进行区域划分,进而在区域内按照网状搜索去寻找邻域像素,并根据邻域像素距离待匹配像素的远近配置权重,进而将这些像素的匹配代价按照对应权重加权聚合起来,完成待匹配像素的代价聚合。
在超像素分割中,采用SLIC算方法。这种算法通过种子点初始化、种子邻域更新、像素点配置标签、距离度量、迭代优化、增强连通性,实现分割,其示意如图2.
从图2可以看出,经过SLIC算法的超像素分割,整个图像平面被划分为多个大小接近的区域,这些区域也比较精确地利用了图像中的灰度和纹理边界,各区域纹理和灰度信息都比较接近,具有较高的关联性。
接下来,在每个区域内执行网状搜索,遍历区域内待匹配像素的关联邻域像素,其搜索过程如图3所示。
在图3中,斜线填充区域为超像素分割获得的区域边界,0号标注的红色像素为待匹配像素,各个黄色像素为最终搜索到的邻域像素。搜索过程按照先横向后纵向的原则进行。以图中的位置为例,从位置0开始,先执行横向搜索,逐次找到1号、2号、3号、4号、5号像素,0号像素的左侧和5号像素的右侧均为区域边界,不与记录。之后,分别从0号、1号、2号、3号、4号、5号像素向上方纵向搜索,只有4号像素上方找到6号像素。之后,从6号像素再分别执行横向搜索和纵向搜索,均为区域边界。之后,分别从0号、1号、2号、3号、4号、5号像素向下方纵向搜索,分别找到7号、8号、9号、10号、11号像素。以此类推,一直找到区域内全部像素。
搜索到区域内的全部像素以后,按照距离待匹配像素的远近,为每一个像素配置权重,具体处理如下:
式中:i为像素标号;ωi为第i号像素的权重;xi、yi为第i号像素的横纵座标;x0,y0表示第0号像素的横纵座标。
最后,将网状聚合窗口内各个像素的初始匹配代价进行聚合,具体处理如下:
2 实验结果与分析
2.1实验数据
为了验证本文提出的基于改进Census变换和网状代价聚合的立体匹配方法对于获得致密视差图像的有效性,进一步展开实验研究。实验中,选择了Middlebury立体视觉评价平台上的4类立体图像,分别是Staircase,Newkuba,Livingroom,Hoops。这4类立体图像由Daniel Scharstein及其合作者采用德国DLR立体视觉传感器拍摄,配置了标准的视差图像,是立体视觉领域通用的测试数据。
为了形成和本文方法的直观对比,在Middle-bury立体视觉评价平台选择了2类方法,分别是Lo-calExp算法、FEN-D2DRR算法。目前,这2类方法的立体匹配性能在Middlebury平台上分别排名第1、4位。
2.2 视差图质量比较
3种方法生成的视差图像质量的视觉效果比较。如图4所示。
图4中,第一列为Staircase图像及其视差图像,第二列为Newkuba图像及其视差图像,第三列为Livingroom图像及其视差图像,第四列为Hoops图像及其视差图像。第a行为四组图像对的左图原始图像,第b行为四组图像的真实视差图,第c行为四组图像采用LocalExp算法获得的视差图像,第d行为四组图像采用FEN-D2DRR算法获得的视差图像,第e行为四组图像采用本文算法获得的视差图像。
从图4中的视差图质量可以看出,本文方法获得了比较理想的稠密视差图像,其效果与目前Mid-dlebury平台上排名第一的LocalExp算法不相上下,都非常接近真实视差图像。
2.3 坏像素占比比较
进一步比较3种方法生成的视差图像中的坏像素情况,如图5所示。
图5中,第一列为Staircase坏像素图像,第二列维Newkuba坏像素图像,第三列为Livingroom坏像素图像,第四列为Hoops坏像素图像。第a行为四组图像对的真实视差图像中的坏像素分布,第b行为四组图像采用LocalExp算法获得的视差图像中的坏像素分布,第c行为四组图像采用FEN-D2DRR算法获得的视差图像中的坏像素分布,第d行为四组图像采用本文算法获得的视差图像中的坏像素分布。
为了进一步直观地比较本文方法和其它4種方法立体匹配过程中坏像素比例的高低,对图8、图9中的坏像素比例进行统计,列在表1中。
3 结论
为了获得连续稠密的视差图像,本文在Daniel立体匹配算法框架的基础上,构建了一种新的立体匹配方法。在初始匹配代价计算步骤,对Census变换方法进行改进,通过剔除极值的方法对亮度差异进行了有效抑制,提升初始匹配代价计算的准确性。在代价聚合步骤,采用SLIC算法对立体像对执行超像素分割,在每个分割区域内采取网状策略搜索聚合像素,提升聚合代价的可信度。选择Middlebury平台上的Staircase,Newkuba,Livingroom,Hoops等4类立体像对作为测试图像,选择LocalExp算法、FEN-D2DRR算法作为本文算法的比较算法,执行立体匹配。实验结果表明,本文算法可以获得连续稠密的视差图像、坏像素比例低,其性能与Middle。bury平台上排名第一的LocalExp算法接近。

