高动态条件下星点像斑建模与补偿*

练 达，周 琦，余路伟，毛晓楠，郑循江

(1.上海航天控制技术研究所·上海·201109； 2.中国航天科技集团公司红外探测技术研发中心·上海·201109)

0 引 言

星敏感器作为现有的精度最高的三轴姿态测量产品，在各类航天飞行器上得到了广泛应用。星敏感器的动态性能是指在航天器以一定角速度转动的情况下，星敏感器对这种转动的适应能力，是星敏感器的一项重要指标。卫星初始入轨、快速机动、大角度调姿等条件下，对星敏感器动态性能提出了很高要求；导弹等其他高机动性航天器对星敏感器的动态性能提出了更高的要求[1]。

星敏感器对恒星成像是光电子在像元上做能量累积的过程，积分时间通常在几十到几百毫秒。因此，在高动态条件下，由于运动模糊，星点能量可能不再是近圆形的高斯分布，而呈现出条带状的星点像斑，称为“拖尾”现象。星点“拖尾”像斑有可能断裂为若干段，采用常规星点提取方法无法准确定位质心；为缩短星点拖尾，减少断裂的可能性，可将曝光时间缩短，但这会导致探测器接收的星点总能量变少，使星点信号湮没在噪声中难以识别。

高动态下的星点像斑提取与质心定位技术对于提高星敏感器动态性能十分重要，近年来有一些学者对此展开研究。针对“拖尾”现象，文献[2]提出一种自适应选取窗口并在窗口中进行星点目标提取的方法，当星体存在断裂时利用数学形态学的方法对星体进行断点判定和补偿，但用于补偿的结构元素和灰度值选择方法较为简单，容易失真；文献[3-4]介绍了不同运动形式下星图的退化模型，通过连续卷积得到退化矩阵，采用分步复原去除星点模糊，但多次采用卷积运算实时性难以保证；针对高动态下的暗弱星点提取，文献[5]提出基于帧间窗口移位叠加灰度增强的方法，提高窗口内弱星信噪比，使其成为可提取的观测星，但此方法主要用于提高弱星探测率，对于质心定位精度没有进行研究与探讨。

针对高动态情况下暗弱星点的提取与质心计算问题，本文提出一种通过相关性匹配提取并补偿动态星点像斑的方法来提高星点提取成功率和质心定位精度。首先，介绍如何建立星点像斑静态模板；其次，结合星点像斑静态模板与星点运动模糊模型建立星点像斑动态模板，以动态模版为基础运用相关性匹配法进行星点提取与补偿。最后通过实际拍摄的高动态星图完成了算法的仿真，验证了其有效性。

1 星点像斑静态模板

恒星成像静态模板为星敏感器在良好工况下的成像模型，即在星敏感器处于飞行平稳、背景噪声情况良好等条件下的成像模型，这也是星敏感器主要的工作状态，在此工作状态下建立星点像斑静态模板[6]。星敏感器的光学系统一般通过离焦技术使星点成像为近圆形的弥散斑，以提高质心细分定位的精度[7]。在理想条件下，像斑的分布近似为二维高斯分布[8]，但由于像差、噪声等干扰因素，实际星点像斑与二维高斯分布存在一定的误差。因此偏正态分布模型比二维高斯分布能够更好地拟合像斑模型，其数学表达形式如式(1)所示。

fstar(x,y)=

(1)

其中fstar(x,y)为像元(x,y)的光电子数；(x0,y0)为像斑能量分布峰值坐标；A1、A2为转换系数；σ1、σ2为高斯半径，表征像斑弥散程度；Nstar为星敏感器接收恒星辐射能量产生的光电子总数，与恒星目标特性、星敏感器响应特性和星敏感器曝光时间等有关，对于特定的恒星及特定的星敏感器，Nstar可视为常数。

随后根据量化等级，可将光电子数转化为灰度值，星点像斑静态模板如式(2)所示。

(2)

其中Istar(x,y)为像元(x,y)的灰度值，n为量化系数，如8 bit，16 bit，M为像元电子满阱容量。

令参数向量v=[A1,A2,σ1,σ2]T，确定参数向量v后即可根据式(1)、(2)建立某一恒星在某型星敏感器上的星点像斑静态模板Istar(x，y)。

星点静态像斑具有灰度总和、像斑所占像元数、像斑最大灰度值等几个主要的特征量。星敏感器成像的输入为确定的恒星目标，其辐射特性可认为恒定不变。星敏感器成像系统的参数虽然会随着器件老化缓慢产生变化，但在短时间内(通常几周或几个月)可视为恒定的。由此，星敏感器成像在一定时间内可视为一个确定的过程，其输出的针对某一恒星的星点像斑是确定的。当恒星划过星敏感器视场时，像斑的形状可能会由于光学系统存在的像差略微发生变化，但星点像斑特征量是稳定的。因此，可以认为星敏感器对恒星成像的像斑及其特征量是平稳的随机过程，对于具体的某台星敏感器和确定的某颗恒星，其成像的像斑及能量分布是稳定的，组成星点像斑的每个像元的灰度为某个确定数值叠加噪声[9]。这一特点使得基于Kalman滤波理论估计像斑的特征量成为可能。Kalman滤波过程如下：

将星点像斑测量模型视为一个随机线性离散系统，其状态方程如(3)所示。

x(k+1|k)=x(k)

(3)

其中x(k)为星点像斑特征向量。

式(4)为测量方程，z(k)为量测信息，即从每帧星图中提取的星点像斑特征。v(k)是测量噪声，其方差R(k)根据工程经验进行估计，本文实验中取R(k)如式(5)所示。

z(k+1)=x(k+1)+v(k+1)

(4)

(5)

在实际在轨飞行中，可通过理论计算得到x(0)作为初值，当星敏感器进入稳定运行阶段后，恒星成像的图像序列可视为平稳的随机过程，可使用该滤波器进行迭代运算，实时输出星点像斑特征x(k)用于确定模型参数。

根据上述计算与滤波结果可得到实际星点像斑特征量，以此作为参考基准，确定偏正态模型参数向量v，即寻找一组参数，使基于偏正态分布模型仿真得到的星点像斑特征量与通过Kalman滤波器得到的星点像斑特征量参考值的误差最小。高精度星敏感器将在长期的在轨飞行中，不断地对其导航星表中的每颗恒星做成像模型参数估计，并更新到导航星表中。

2 星点像斑动态模板与配准补偿法

在高动态条件下，星点提取具有以下两个难点：

(1)在曝光时间较短的条件下，星点像斑“拖尾”不显著，且不易断裂，但星敏感器接收到的星点总能量减少，而动态条件下星点能量被分配到更多的像元上，导致单个像元接收能量相对于静态条件下变少，使得星点可能湮没于噪声信号中难以识别，这对于暗弱星点目标尤其明显。同时在星敏感器寿命末期，由于噪声增多，信噪比降低，这一问题会更加突出，如图1(a)。

(2)曝光时间较长的条件下，接收到的星点总能量增多，导致“拖尾“较长，可能出现断裂、残损等情况，如图1(b)，使目前常用的星点提取方法(连通域算法)失效，并且缺失部分信息会导致星点质心定位精度降低。

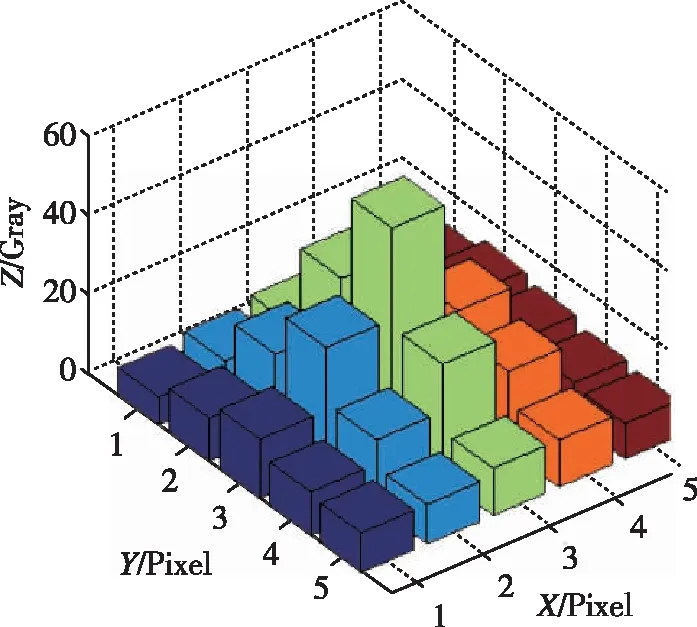
(a)暗弱星点像斑

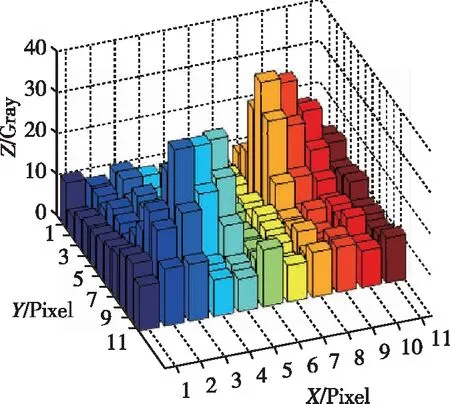
(b)断裂星点像斑图1 两种典型的动态星点像斑Fig.1 Two types of typically star spots in high dynamic conditions

针对上述难点，本文提出一种基于相关性匹配的星点配准与补偿方法。该方法可分为四步：(1)建立星点像斑动态模型。(2)根据星敏感器运动信息预测星点成像波门位置。(3)在波门中使用模板匹配法找到相关性最大区域，视其为星点所在区域。(4)根据模板补偿星点断裂或残损部分，用灰度加权的质心法计算星点质心。

2.1 建立星点像斑动态模型

在得到星点静态成像模型Istar(x,y)后，通过陀螺得到的星敏感器载体运动信息结合星点运动模糊模型[10]，可得到旋转运动模糊长度Lxy为

Lxy=fωxyδt/d

(6)

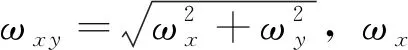
(7)

退化函数hRP(x,y)为

hRP(x,y)=

(8)

通过卷积得到星点动态成像模型

w(x,y)=I(x,y)⊗hRP(x,y)

(9)

w(x,y)即为星点成像模板。

同时，根据星敏感器载体运动信息及连续多帧星图的星点质心轨迹，可预测星点质心下一时刻出现的位置。以此为中心取32×32个像素的波门为匹配区域。星敏感器动态情况下的星点像斑长度一般控制在20个像素之内，因此该波门大小能够包络整个星点像斑。后续算法的处理均在此波门中进行。

2.2 星点配准方法

基于相关的模板匹配技术是一种图像处理技术，其可用于在一幅图像中寻找某种子图像模式[11]。对于大小为M×N的图像f(x,y)和大小为J×K的子图像模式w(x,y)，f与w的相关可表示为：

c(x,y)=

(10)

其中，x=0,1,2,…,N-K,y= 0, 1, 2,…,M-J，坐标系原点均位于图像的左上角。

计算相关c(x,y)的过程为在图像f(x,y)中逐点地移动子图像w(x,y)，使w的原点和点(x,y)重合，随后计算w与f中被w覆盖的图像区域对应像素的乘积之和，以此计算结果作为相关图像c(x,y)在(x,y)点的响应，其只和图案模式本身的形状或纹理有关，与幅值(像素灰度)无关。在模板移过整幅图像f后，最大的响应点(x0,y0)即为最佳匹配的左上角点。

以1.1节中所得的星点像斑模板为子图像w(x,y)，波门图像为f(x,y)，依据上述公式与方法计算得到最佳匹配点(x0,y0)，以(x0,y0)为左上角的J×K大小的区域即为星点所在区域s，即

(11)

在动态条件下，即使星点像斑存在断裂和部分像元淹没在噪声中这两种情况，由于星点像斑主体能量分布趋势不变，模板能够与之匹配，因此可以正确提取星点像斑。

2.3 星点补偿方法

高动态条件下，由于星点像斑断裂及部分像元淹没在噪声中，丢失了部分星点像斑图像信息，导致星点质心定位精度降低。因此，需要对星点像斑进行补偿，提高星点质心定位精度。

首先对星点所在区域s进行背景滤波[12]，选取s外围一周的像元背景估计中心点背景，有

(12)

式中，P为背景估计模板，pij为各点对应权值。

在估计背景并滤波后可得到残差图像s′。将动态星点像斑模板w上存在星点能量的像元与残差图像s′一一对应，可得到残差图像s′理论应该存在星点能量的像元。将s′内不存在星点能量的像元灰度置0，得到只存在星点像斑的图像s″。计算s″与w像元灰度比例α，有

α(x,y)=

(13)

依据式(14)进行星点像斑补偿

s″(x,y)=

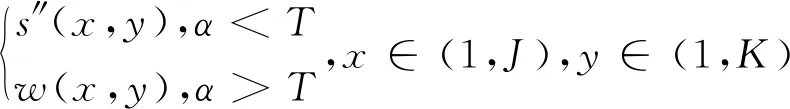
(14)

其中阈值T可依据工程经验确定。

在补偿完毕后，利用灰度加权的质心法进行星点质心定位，得到星点质心在s″内的坐标

(15)

根据前文所得s″区域在背景星图f(x,y)中的坐标，可得星点质心坐标(xc,yc)为

(xc,yc)=(xc′,yc′)+(x0,y0)

(16)

3 实验验证与分析

3.1 实验条件与准备工作

实验分为两组，第一组实验采用本文提出的配准与补偿法处理星图，第二组实验采用传统的阈值分割与连通域法处理星图。

实验采用的星图数据为某型号星敏感器外场观星数据，数据分为A、B两组，为同一台星敏感器在不同时间对于不同天区观星所得，因此A、B两组数据涉及到的恒星信息不相同，星敏感器器件参数相同。

A组观星数据为地速条件下星敏感器观星数据，用于建立恒星成像模型并迭代优化模型参数，星敏感器可视为静止状态。

B组星敏感器安装于转台上，为动态条件下星敏感器观星数据，用于验证高动态条件下恒星模型对于星敏感器姿态精度提升效果，B组实验条件如下：

(1)星敏感器三轴角速度约为ωx= 1.50[(°)/s]，ωy= 1.50[(°)/s]，ωz= 0[(°)/s]，合成角速率ωs= 2.12[(°)/s]，与x轴夹角为θ= 145°，实际速度以测量值为主；

(2)由于转台自身误差，每一帧的三轴角速度会略微有所偏差，选取其中较为平稳的100帧观星数据作为实验数据；

(3)曝光时间t=100 ms；

(4)总时长为10 s，即100帧图像；

(5)由于星敏感器软硬件条件限制，获取的波门图像灰度矩阵信息为8 pix×8 pix大小；

(6)星敏感器焦距为f=52 mm；

(7)探测器像元尺寸为dx=dy=d=18×10-3mm；

(8)在实际星图中，坐标系为星敏感器测量坐标系，在图像处理时为便于处理，以图像左上角为原点，x轴为矩阵行方向，向右为正方向，y轴为矩阵列方向，向下为正方向。

由于星敏感器在动态条件下划过视场的天区较大，视场中出现的恒星较多。地速条件下观星时只对准一片固定的天区，无法覆盖到动态条件下划过的所有天区。即在外场观星中，无法得到动态条件下所有定姿星的静态星点像斑图像，无法直接对动态条件下的所有定姿星进行模型迭代优化过程。因此，仿真实验中将A、B两组跟踪星进行分类，选取其中合适的A组跟踪星作为代表星，建立代表星的成像模型，用此成像模型作为此类恒星的成像模型用于B组实验。

由于实验条件限制，星敏感器下传的数据包内储存的波门图像只有8 pix×8 pix大小，如图2所示，而计算得到的星点模糊像斑长度在10 pix以上。这导致有一部分的星点像斑可能在波门图像之外未被截取。并且，若直接在波门图像内以星点模糊像斑作为子图像进行匹配，两者大小接近甚至相同，会导致模板匹配无法进行。因此需要对波门图像进行扩充以满足模板匹配的要求。

选取没有星点像斑存在的背景图像区域作为填充像素，随机填入32 pix×32 pix大小的图像灰度矩阵中。设定此灰度矩阵中的6至13行与6至13列重叠区域为星点像斑区域，将波门图像填入其中，作为实验原图像I0(x,y)，如图3(a)所示。为方便显示，截取其1至16行与1至16列重叠区域显示灰度矩阵。

(a)波门图像

(b)图像灰度矩阵

(a)波门图像

(b)图像灰度矩阵

将所有波门图像进行处理，以I0(x,y)为新的波门图像，在I0(x,y)内进行星点识别、提取与补偿等后续处理。

3.2 建模、复原及质心提取

由图3可见，在高动态条件下，星点模糊像斑在背景图像中已经难以识别，采用阈值分割与连通域判定相结合的方法，无法从背景中将星点像斑分割并提取。

令星点静态像斑模板为f(x,y)，依据式(6)～(9)及实验条件可建立高动态下星点像斑成像模型g(x,y)，如图4所示

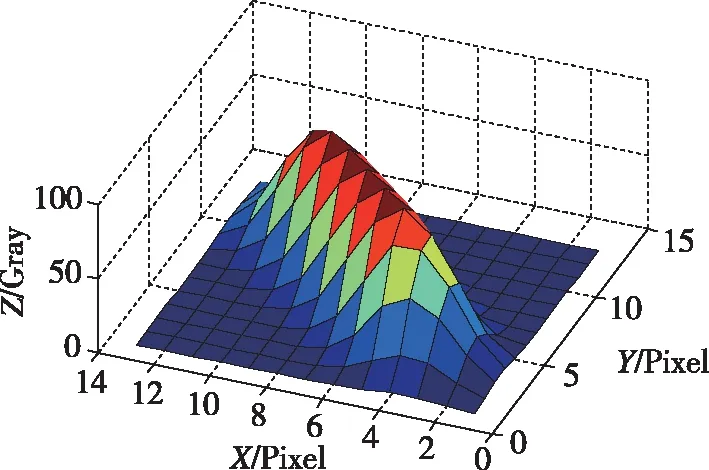
(a)成像模型

(b)灰度矩阵

图4 星点动态像斑模板

Fig.4 Dynamic star spot model

以星点动态像斑模板为子图像，利用模板匹配法在原图像I0(x,y)内寻找相关性最大的区域，并得到星点像斑所在区域s″。由于实际观星实验存在大气环境等实际观星条件差异，星点动态像斑模板与实际动态星点像斑之间会存在灰度差异，但其像斑灰度能量分布特征不变，因此不能直接使用星点动态像斑模板补偿实际像斑。为消除这种灰度差异，选取模型中灰度值最大的三个像素，与实际像斑中灰度值最大的三个像素求取比例，按比例调整模板灰度值后再进行补偿，补偿后提取星点质心坐标信息。

3.3 实验结果与分析

绘制100帧图像的星点质心变化轨迹，应用配准与补偿法所得结果如图5(a)所示。图5(b)为阈值分割与连通域法所提取的星点质心坐标轨迹，图5(c)为配准与补偿法轨迹对照图，其中蓝点为配准与补偿法提取质心坐标，红点为导航星质心坐标，即坐标位置参考值。

(a)配准与补偿法质心坐标

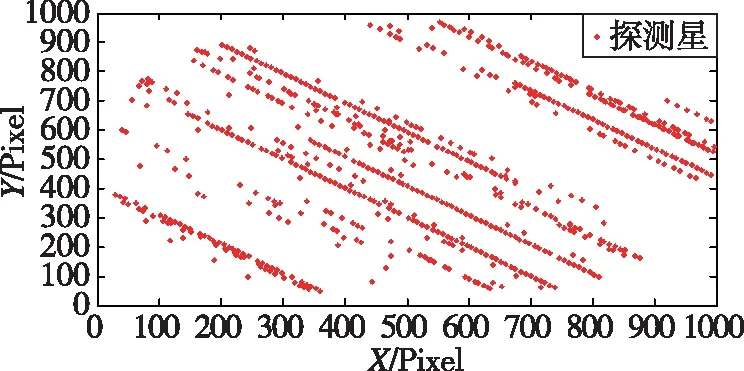
(b)阈值分割与连通域法质心坐标

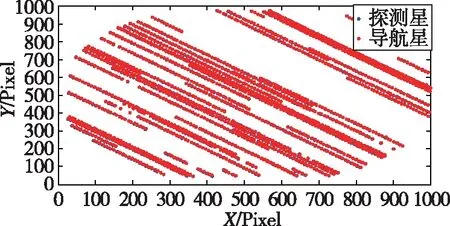
(c)配准与补偿法质心坐标对比图5 星点质心轨迹图Fig.5 Star centroid trajectory

由图5可见，阈值分割与连通域相结合的方法，在高动态条件下星点提取率不高，大多数星点质心轨迹存在断裂；而配准与补偿法星点提取率极高，且精度较高，实验星点质心轨迹与参考星点质心轨迹拟合较好。

采用星间角矩法计算100帧姿态精度误差epos，并求取平均姿态误差与最大、最小姿态误差，结果如图6与表1所示。

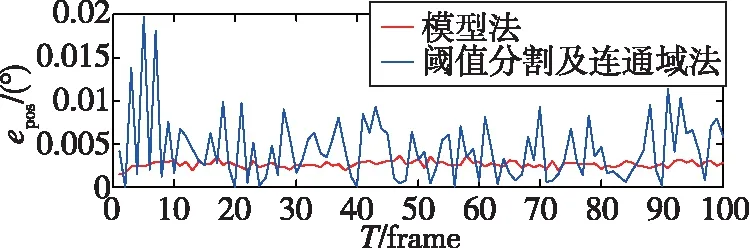
图6 姿态精度误差比较Fig.6 Comparison of attitude accuracy errors

表1 姿态精度误差/数据有效率统计

Tab.1 Attitude accuracy error/data effective rate statistics

算法姿态精度误差/(°)均值最大最小配准与补偿法0.00260.003700.00150阈值分割与连通域法0.00440.019700.00002

由图6与表1可见配准与补偿法的姿态精度误差较为稳定，且普遍低于阈值分割及连通域法，姿态精度误差均值减少了40.9%，最大误差减少了81.2%。从数据有效率方面来看，配准与补偿法能够稳定输出姿态信息，阈值分割与连通域法不稳定，会出现跟踪失败的情况。配准与补偿法姿态精度误差平均为0.0026°，即9.36″，满足星敏感器精度要求。

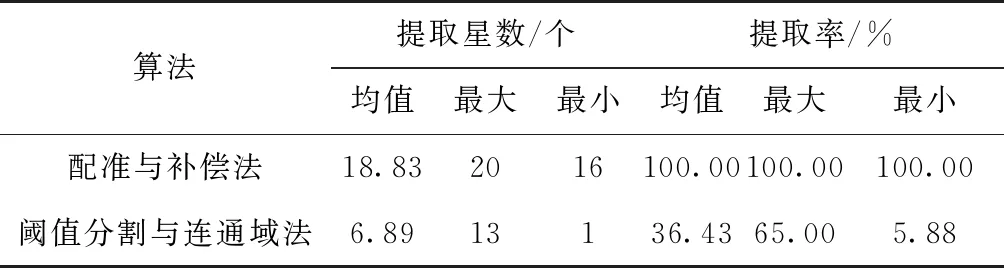
表2 单帧提取星数/提取率统计

表2为100帧内两种算法的单帧提取星数与提取率。由表2可见，配准与补偿法提取星数能够稳定地提取星点，提取率达到100%，相比阈值分割与连通域法提高174.5%，提取星数相比阈值分割与连通域法提高了173%；阈值分割与连通域法提取率较低且不稳定。说明恒星成像模型能够有效帮助提高星点提取率，星点提取率直接影响到星敏感器姿态精度与跟踪稳定性。

4 结 论

本文针对高动态条件下星点像斑提取的难点，提出了一种星点的提取与补偿方法，此方法通过建立动态条件下的恒星成像模型，利用图像处理中的模板匹配法提取星点，能够有效提取断裂星点像斑与暗弱星点像斑，并利用模板补偿星点像斑的断裂部分或边缘缺失部分，有效地提高了星点质心定位精度。基于外场观星数据的仿真实验验证，相比传统算法，本文提出的方法姿态精度误差均值减少了40.9%，最大误差减少了81.2%；星点提取率达到100%，提高174.5%，提取星数相比阈值分割与连通域法提高了173%。