基于粒子群寻优的高精度星敏感器在轨标定方法*
张 刘,张家坤,吕雪莹,范国伟,章家保,满益云
(1.吉林大学 仪器科学与电气工程学院·长春·130061; 2.钱学森空间技术实验室·北京·100094)
0 引 言
星敏感器是一种以恒星为参照系,以星空为工作对象的高精度空间姿态敏感器[1],具有定位精度高、质量小、功耗低、高度自主,并且无姿态累积误差等优点[2]。但星敏感器在工作过程中会受到像平面主点、主距、倾斜与旋转等多种误差源的影响,这些误差的耦合将使得星敏感器的在轨标定工作变得极其困难,如何提高星敏感器的标定精度成为科研人员的研究热点。
国外关于星敏感器在轨标定技术的研究起步较早,1981年,Shuster M D和Oh S D开创性地研究了敏感器安装误差的标定,打破了星敏感器标定只能在地面完成的壁垒[1]。2001年,Ju[3]提出基于星对角距的恒星检校方法,该方法采用星对角距的正弦相等的原理对星敏感器的内参数进行了检校[4],有效地提高了星敏感器的标定精度。2013年~2014年,Pal M[5-6]提出了两种方法。第一种方法为自主标定法,利用多幅星图中的星点坐标信息进行标定,第二种方法基于最小二乘法,利用赤经赤纬星点信息对姿态和相机参数同时估计[1]。2015年,Zhou[7]利用最优化理论对星敏感器光学畸变和光学参数进行了多步标定,其方法精度相较于最初的Samaan方法有很大提升。
国内关于星敏感器在轨标定技术的研究起步晚于国外,但近年来发展迅速。2008年,袁彦红等[8]由最小二乘最优估计法在轨标定星敏感器星像点偏移和光学透镜焦距变化,以最小二乘最优估值为量测, 用卡尔曼滤波算法设计了星敏感器在轨自主标定模型,结果表明,该方法可准确标定星敏感器星像点偏移和透镜焦距变化。2010年王跃钢等[9]提出了捷联惯导/星敏感器组合系统中对陀螺仪和星敏感器进行在轨自标定的方法,仿真结果表明,基于卡尔曼滤波的在轨自标定方法能够标定出85%以上的陀螺仪随机常值漂移和95%以上的星敏感器安装误差。2014年,魏新国等提出了针对星敏感器的内外参数标定法,其研究表明该方法可有效提高定姿精度[10]。2019年崔航等[11]通过绕陀螺仪三个敏感轴方向的姿态激励实现对陀螺仪工具误差以及初始对准误差和星惯安装误差的在线标定,通过对惯性器件测量结果的修正,抑制导航误差。仿真结果表明,在线标定方法可以实现对上述误差参数的在线标定,具有一定的工程实用价值。
本文提出一种基于粒子群算法的星敏感器在轨标定方法,与传统标定方法的优势在于它不需用陀螺对星敏感器进行标定,而是直接利用星敏感器像平面的坐标来进行标定,减少了陀螺所带来的误差,有效地提高了标定精度。
1 星敏感器标定过程
1.1 星敏感器理想成像模型
星敏感器成像的理想模型是小孔成像模型[12],在天球中,恒星发出的平行光通过星敏感器的光学镜头在其像平面上呈现一个光斑。星敏感器的成像模型如图1所示:
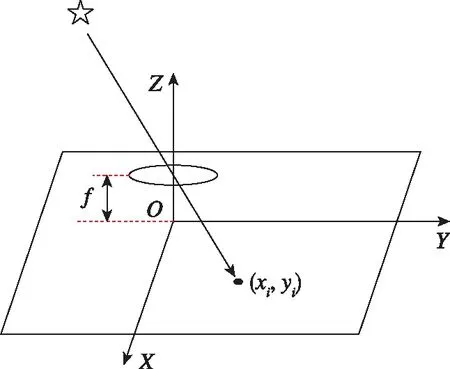
图1 星敏感器理想成像模型Fig.1 Ideal imaging model of star sensor
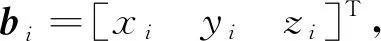
(1)
(2)
恒星在天球坐标系上的赤经赤纬为(α,δ),恒星在天球坐标系下的参考矢量ri为:
(3)
当星敏感器无误差时,恒星在星敏感器坐标系中的星光矢量为:
(4)
星敏感器在工作过程中会产生诸多误差,主要分为像平面主点误差、旋转误差、倾斜误差与主距误差,这些误差会使星光矢量投影在CCD像平面中的坐标发生误差,进而影响星敏感器的测量精度。当星敏感器存在误差时,星光在星敏感器坐标系中的矢量为:
Wi=
(5)
其中(x0,y0,f0)为(xi,yi,fi)经过星敏感器综合误差产生的偏移量。
1.2 星敏感器误差模型
当星敏感器含有主点、主距、倾斜与旋转四种误差时成像模型如下所示[13]:
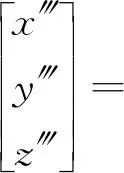
(6)
(7)
(8)
其中:(x‴,y‴,z‴)为真实像点在无误差星敏感器坐标系下的坐标,η为星敏感器像平面倾斜的角度,设像平面绕单位矢量(a,b,0)倾斜,ψ为星敏感器像平面旋转的角度,(x0,y0)为主点的偏移量,(x,y)为含有误差的像平面的坐标,(xnew,ynew)为校正后像点坐标。
校正后的观测矢量为:
(9)
已知观测矢量bi与参考矢量ri,通过Quest算法可以计算出星敏感器三轴姿态角θ(俯仰角)、φ(滚转角)、ψ(偏航角)计算精度可由式(10)求得。
(10)
1.3 Quest算法
几乎所有基于矢量观测的姿态确定问题都可以归结为Wahba问题。在1965年,Wahba提出利用矢量观测信息确定航天器的姿态问题,其核心是求解行列式为+1的最优正交矩阵,构造损失函数[14]
(11)
其中ai为非负的权重系数,ri是相应的参考系中的单位矢量。利用矩阵迹的轮换不变性,整理式(11)可得:
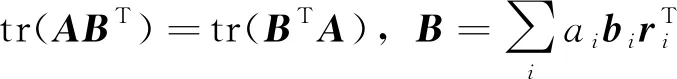
将姿态矩阵A写成四元数形式:
将上式代入得:tr(ABT)=tr(BTA)
(12)
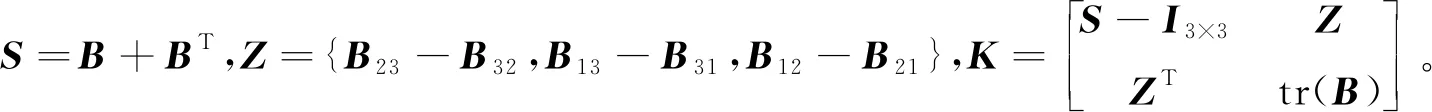
式(12)可进一步转化为:
Kqopt=λmaxqopt
(13)
由式(13)可知,最优四元数可以表示为:
(14)
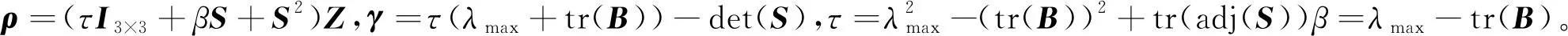
λmax可由方程(15)通过牛顿迭代法求出:
λ4+(κ+ξ)λ2-μλ+(κξ+μσ-d)=0
(15)
其中:κ=(tr(B))2-tr(adj(S)),ξ=(tr(B))2+ZTZ,μ=det(S)+ZTSZ,d=ZTS2Z,σ=tr(B)。
2 基于粒子群算法的标定流程
2.1 粒子群算法原理
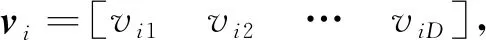
vil=wvil+c1r1(pil-xil)+c2r2(pgl-xil)
(15)
xil=xil+vil
(16)
式(15)中w是权重系数,c1,c2为加速常数,r1,r2为[0,1]内的随机值,式(15)中vil与xil分别是第i个粒子第l维的速度与位置。pil表示第i个粒子的个体极值中第l维的值,pgl表示全局最优值中第l维的值。另外,考虑到粒子速度应在合理范围内,分别可设定速度上限Vmax和速度下限-Vmax。在公式(15)中的第1部分为粒子“旧”速度部分;第2部分是“认知”部分,表示粒子自身的思考;第3部分为“社会”部分,表示粒子之间的信息共享与合作[16]。
2.2 基于粒子群算法的标定步骤
(1)已知在含有误差的情况下星光在星敏感器像平面上的坐标为(xi,yi),i=1,2,3(以3颗星为例)。估计星敏感器含有误差的像点坐标与无误差时像点坐标差值的范围,设置相应参数并初始化种群。
(2)通过初始化的种群对(xi,yi)进行误差补偿,得到新的像点坐标(x′i,y′i),i=1,2,3,在此基础上得出校正过后的观测矢量b′i,带入Quest算法得出三轴姿态角。将解算出的姿态角带入目标函数F中,计算F的值。目标函数为:
(17)
其中:θ′、φ′、ψ′为矫正后的姿态角,θ、φ、ψ为没有误差时的姿态角。
(3)分别将粒子当前的F与自身最优值和全局最优值进行比较,如果粒子当前值的F比自身最优值更优,则粒子当前值替代成为新的自身最优值,类似的,粒子当前值的F比全局最优值更优,则粒子当前值替代成为新的全局最优值。按照公式(15)和公式(16)更新粒子的位置和速度,产生新的种群。
(4)若F小于给定精度或达到最大迭代次数,则程序停止,得出F的最小值,此时的(x′i,y′i)为在此误差范围内,最接近无误差的像点坐标。
(5)根据含误差的观测矢量与校正后的观测矢量求出误差像平面与虚拟像平面的姿态矩阵。
3 仿真试验及结果分析
令天球坐标系X轴、Y轴、Z轴均旋转60°与星敏坐标系重合,则无误差时参考矢量bi为:
给星敏感器加表1所示误差:

表1 误差分布
含有误差后的观测矢量b′i为:
此时的三轴姿态角为:
θ=60.008333972371750φ=60.001596402881255ψ=59.996040471943220
利用粒子群优化算法进行标定得出欧拉角,连续运行5次,结果如表2所示:

表2 标定结果
由表2可知,当星敏感器坐标系与天球坐标系之间的三轴姿态角均为60°,标定精度达到10-10角秒量级,且程序运行稳定。
五次标定过程中,星敏感器误差像平面与虚拟像平面之间的姿态矩阵分别为:

令天球坐标系X轴、Y轴、Z轴均旋转45°与星敏坐标系重合,给星敏感器加表3所示误差:

表3 误差分布
利用粒子群优化算法进行标定得出欧拉角,连续运行5次,结果如表4所示:

表4 标定结果
由表4可知,当星敏感器坐标系与天球坐标系之间的三轴姿态角均为45°,标定精度达到10-10角秒量级,且程序运行稳定。
五次标定过程中,星敏感器误差像平面与虚拟像平面之间的姿态矩阵分别为:

综上所述,当星敏感器坐标系与天球坐标系之间的三轴姿态角为不同角度时,均可精确标定三轴姿态角,精度可达10-10角秒。
4 结 论
提高星敏感器在轨标定的精度是当下的研究热点,本文针对这一问题提出了一种基于粒子群算法的星敏感器在轨标定方法,同时详细阐述了该标定流程。经仿真可知,该方法提高了星敏感器的标定的精度,精度可达10-10角秒,具有较大的工程实用价值。但本文未考虑其它误差源,比如星敏感器镜头畸变、温度等。因此后续将研究关于镜头畸变与温度对星敏感器标定精度的影响。

