遗传算法在通信卫星轨道优化设计中的应用*

邓武东，陈 锋，成 飞，赖 京

(1.上海卫星工程研究所·上海·201109； 2.上海航天技术研究院·上海·201109)

0 引 言

中低轨增强通信是对常规静止轨道卫星通信手段的补充，主要有针对目标区域的大椭圆通信和全球低轨移动星座通信。美国“战术星”-4是一种大椭圆通信卫星，它在频段的选择、通信体制的设计上，能够与其现役或后续规划的UHF通信星形成配合或者在能力上进行增强，并且可对特定目标区域提供一定能力的连续通信支持。构建基于区域型应用的星座系统，可为目标地区提供准实时的空间服务。为了解决大椭圆通信卫星星座设计问题，陈锋等提出通过粒子群算法[1]对星座的轨道参数进行优化，但未寻找到全天时通信星座。相对于粒子群算法多用于连续问题的求解[2]，遗传算法(Genetic Algorithm)还可用于对离散问题的求解，且收敛性分析方法较为成熟。在科学和工程领域常用的遗传算法可用于非线性、不可微和多峰值的复杂优化，于亮等利用遗传算法[3]实现对导航星座轨道参数的优化设计，优化参数为全轨道参数，模型计算复杂；ASGARIMEHR M以定位精度作为评价函数优化了导航星座设计[4]，评价函数的计算稍显复杂。其他智能算法在航天器任务设计中也有着广泛的应用[5-7]，本文以局部重点通信地区为例，基于改进的遗传算法提出了一种大椭圆通信卫星星座轨道参数的优化方法，模型计算量小，且逐代提升效能，收敛速度快。

1 通信卫星轨道的初始模型

大椭圆通信卫星远地点可选择运行在北极方向，可以实现轨道运动的大部分时间对北半球重点区域建链通信，以西太平洋作为局部重点通信地区，进行大椭圆通信卫星轨道的设计优化。

1.1 轨道与星座设计

轨道设计的任务是在载荷、星座规模一定的条件下实现对目标区域的24小时实时通信支持。下文给出了设计输入和设计目标，并阐述了关键轨道参数的选择过程。

(1)输入条件

卫星轨道与星座设计的输入条件为：

①目标地区：西太平洋区域为目标通信站；

②通信仰角：10°；

(2)设计目标

轨道与星座设计目标如下：

①对目标地区24小时不间断访问；

②卫星的数量最少；

③载荷的作用距离最短；

(3)轨道倾角选择

图1给出了近地点幅角随倾角在60天的变化情况，若采用30°低倾角，近地点幅角60天变化增加了113°，对于轨道覆盖性能影响巨大，不可接受，因此须采用倾角为63.43°的临界轨道冻结近地点幅角。

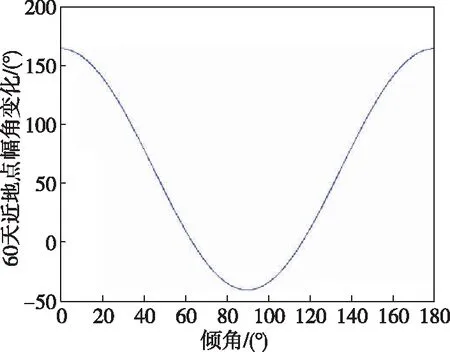
图1 近地点幅角随倾角变化情况Fig.1 Peripheral angle change with different inclination

(4)轨道高度选择

考虑大气阻力的影响，轨道近地点高度暂定为658km。椭圆轨道的回归圈数与轨道高度以及对应的载荷作用距离如表1所示。在载荷作用距离约束下，可根据表1选择合适的轨道高度和回归天数。

初步选择回归圈数为6圈的天回归轨道、远地点高度在12093km左右的这条轨道。

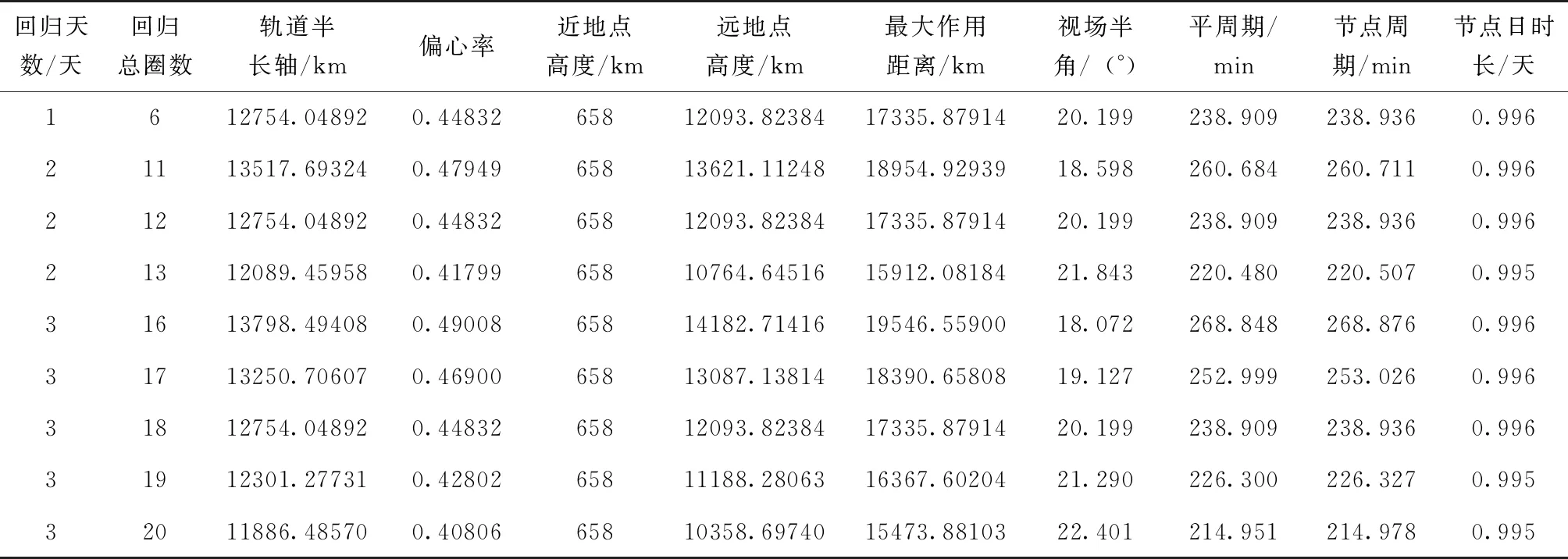
表1 椭圆轨道高度参数

1.2 星座初步方案及效能

在前述1.1节中，阐明拟采用大椭圆临界倾角回归轨道，利用卫星在远地点附近运行速度慢、运行时间长的特点以及回归特性，再配合波束扫描能力或卫星的姿态机动能力，实现对目标区域的长时间通信覆盖。结合通信载荷能力最远约20000km的通信能力，单星轨道具体参数如表2所示。

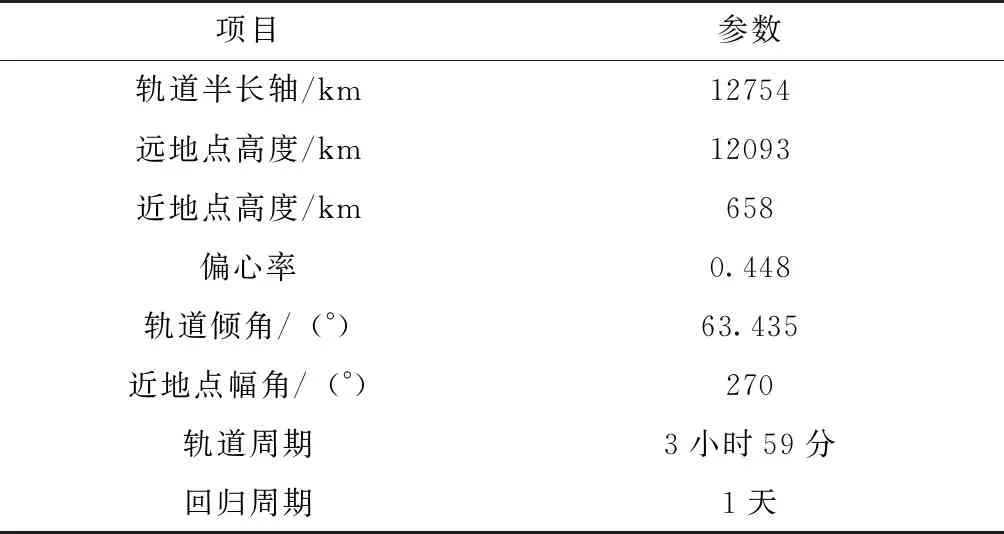
表2 椭圆轨道参数

(1)单星覆盖性能

卫星轨道周期约为4小时，每天运行6圈，星下点轨迹每天重复。如下图2和图3所示，对目标区域一天能形成四个时段的覆盖，总时间可达约7.5小时。其中连续三轨每轨理论覆盖时间超过2小时。因此，理论上只需要四颗星，通过相位和升交点赤经的配合设计，即可实现对目标区域的24小时连续覆盖。

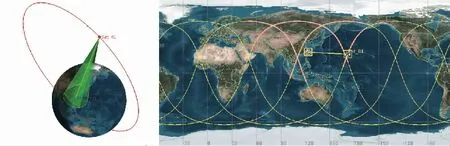
图2 椭圆轨道单星目标区域覆盖特性Fig.2 Single star’s coverage characteristics of elliptical orbit for target area

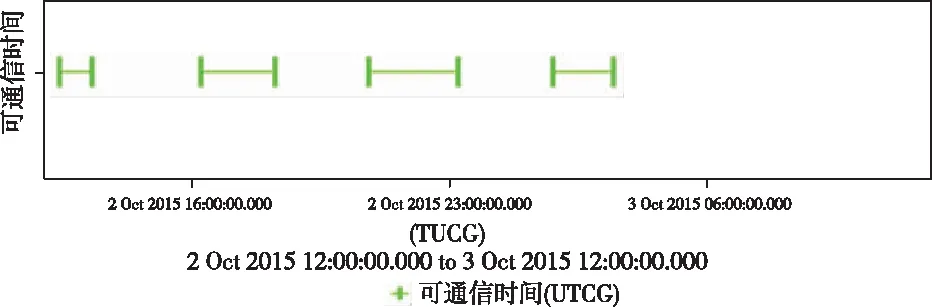
图3 椭圆轨道单星目标区域覆盖时间Fig.3 Single star’s coverage time of elliptical orbit for target area

(2)双星共面椭圆轨道星座覆盖性能分析

采用上述轨道参数，配置共轨道面但相位相差180°的两颗大椭圆通信卫星，轨道参数如表3所示。

表3 双星星座配置方案

采用双星接力，提供对地通信能力的方式，其覆盖形式及特性如图4所示:

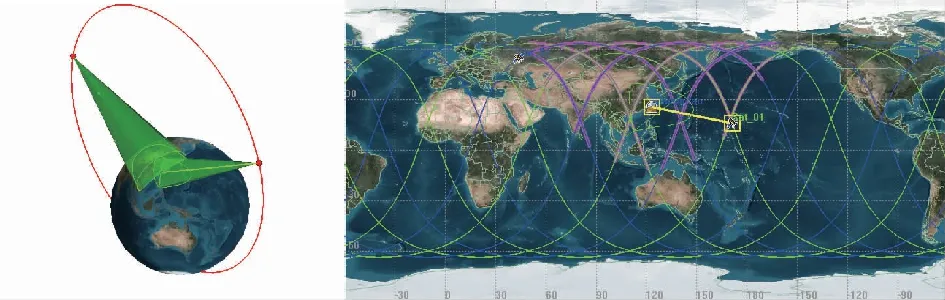
图4 椭圆轨道双星目标区域覆盖特性Fig.4 Double star’s coverage characteristics of elliptical orbit for target area

图5 椭圆轨道双星目标区域覆盖时间Fig.5 Double star’s coverage time of elliptical orbit for target area

由图5可知，相位相差180°的两颗大椭圆通信卫星在上述椭圆轨道上接力工作，可对地提供近15小时的准连续通信能力。

(3)四星准全天通信覆盖星座设计

进一步，为了实现准全天通信要求设计大椭圆通信卫星星座方案。椭圆轨道参数不变的前提下，布置两个轨道面，每个轨道面上部署两颗相位相差180°的大椭圆通信卫星，轨道参数如表4所示。覆盖特性如图6及图7所示，可实现准全天的通信覆盖。

表4 四星星座配置方案

图6 椭圆轨道四星目标区域覆盖特性Fig.6 Four star’s coverage characteristics of elliptical orbit for target area

图7 椭圆轨道四星目标区域覆盖时间Fig.7 Four star’s coverage time of elliptical orbit for target area

根据上述轨道、星座仿真及覆盖特性分析形成如下结论：

①单星椭圆轨道每天可提供3～4次通信覆盖窗口，最多对目标区域提供2.5小时的连续覆盖通信时间；

②椭圆轨道两星共面接力通信每天可提供超过12小时的准连续通信覆盖能力，在同一个轨道面上增加卫星数量对提高连续覆盖能力贡献不大；

③采用两个轨道面，每个轨道面上部署两颗相位相差180°的大椭圆通信卫星，可实现准全天连续对目标区域的通信覆盖能力。

2 方案选择与优化

上述四星方案的升交点赤经和相位的布置还不是最优的，接下来通过增加了保优算子的改进的遗传算法寻找到最优布置，并且按照该布置方案设计24小时无缝覆盖的通信星座。

2.1 待优化参数

在高度、偏心率、倾角、近地点幅角给定的情况下，待优化参数包括两轨道面升交点赤经，四颗星相位，将待优化参数作为遗传算法编码对象[8]，如表5所示。

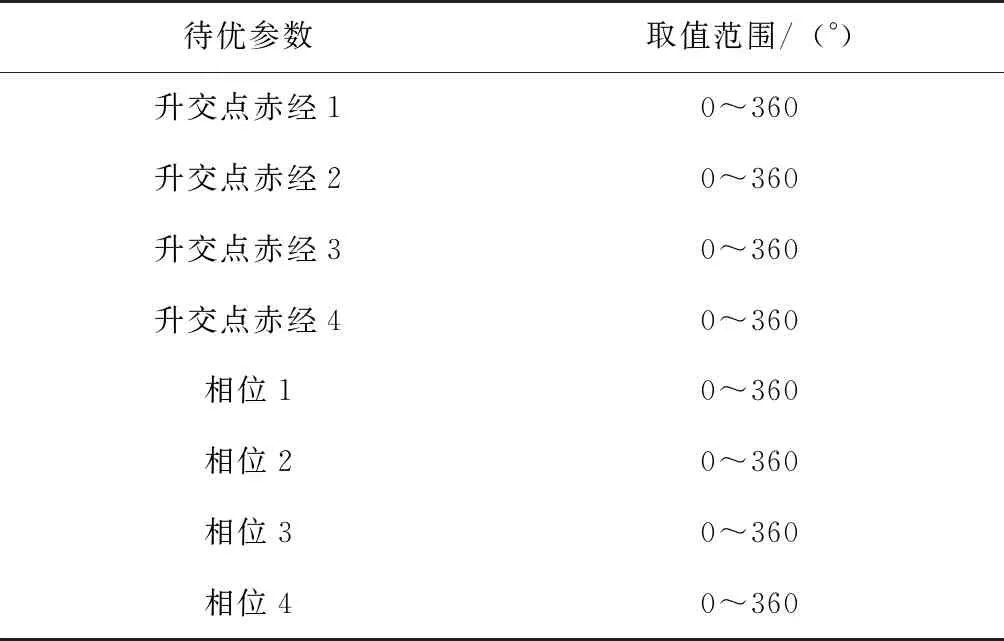
表5 遗传算法待优化参数

2.2 遗传算法优化方法

遗传算法是一种模拟自然界进化过程的优化算法。它利用编码技术将对象转换成自然界中个体的染色体形式，通过设计相应的遗传算子来操作由这些个体组成的种群，从而达到模拟生物种群进化过程的目的。本文将采用遗传算法对星座的布置进行优化求解。

2.2.1 适应度函数

类似文献[9]基于指标的多目标搜索方法，本文以适应度函数作为评价指标。适应度函数是遗传算法收敛性和稳定性的关键因素之一，对最终的优化结果也有重要影响。因此，本文以通信覆盖的总时间作为适应度函数。

f=ttotal

2.2.2 遗传算子

常规遗传算子通常包括选择算子、交叉算子和变异算子[10-13]。为提高算法收敛性和求解的全局最优性，本文还提出了保优算子。下面将针对这四个算子进行设计。

(1)选择算子

通过选择算子选出种群中较优的个体形成一个新的种群，可使得种群中的个体不断逼近最优解。选择算子可采用常用的轮盘算法，设定个体被选中的概率如下，

(1)

式中fj为个体j的适应度值，n为种群数目。

在上述选择方式下，个体的适应度值越大，被选择的概率也越大，则其基因构造被遗传到下一代的可能性越大。这种选择方式使得种群中的个体都存在被选中的概率，保证了较小个体的遗传性。

(2)交叉算子

交叉是指按交叉概率从种群中选择部分个体，通过交换个体部分基因形成新的个体，从而形成新的种群。交叉算子可采用双点交叉算子。由于个体采用实数编码，所以交叉操作采用实数交叉法，如式(2)所示，第k个染色体ak和第l个染色体al在j位的交叉操作方法为：

akj=akj(1-b)+aljbalj=alj(1-b)+akjb

(2)

其中akj代表第k个染色体ak在j位的值，b是[0,1]区间的随机数。

(3)变异算子

变异算子模拟的是生物进化过程中的基因突变现象，具体操作为：令变异概率为Pc，则变异的节点个数为[nSPc]，S为单个个体的节点数；根据生成的随机数r决定变异方向，选中某些个体上的某些节点，然后用新值替代这些节点上的原值。新值的产生过程如式3所示。变异算子维持了群体的多样性，有利于防止早熟现象的出现。

aij=aij+(amax-aij)kb,r>0aij=aij+(amin-aij)kb,r<0

(3)

其中aij代表第i个染色体ai在j位的值，amax和amin代表a的上下边界值，k是变异系数，b是[0,1]区间的随机数，r是[-1,1]区间的随机数。

(4)保优算子

通过上述三个算子的操作后，种群将由原来的父代变成性能更为优异的子代。但是仍无法保证父代种群中最优秀的个体能全部被遗传到子代种群，从而降低了获得最优解的收敛速度，甚至导致最后寻求到的最优解只是局部最优，而非全局最优。文献[14-15]的常规选择算法都陷入了局部最优的情况。因此，本文提出了一种具有“保优”思想的保优算子。其基本思想是：完全保留父代种群中适应度值最大的部分个体至子代种群。具体操作方式为：分别对父代种群和子代种群中的所有个体按适应度值的大小降序排列，若保优率为Pa(大约为5%～10%)，则父代种群中适应度值排在前[nPa]个的个体将完全取代子代种群中适应度值排在后[nPa]个的个体，形成一个性能更为优异的子代，其中[]表示取整，不同于文献中只保留父代最优个体的保优方法[16]，本文的方法保优率可调，更为灵活。

2.2.3 算法流程

本文算法的计算步骤如下：

(1)生成初始化种群；

(2)根据设计的适应度函数，计算该代种群中所有个体的适应度；

(3)判断是否满足终止条件，若不满足则到步骤(4)，若满足则到步骤(5)；

(4)根据交叉概率和变异概率，经过选择算子、交叉算子、变异算子和保优算子产生下一代种群，然后返回步骤(3)；

(5)选出最后一代种群中的最优个体，输出相应的最优解，算法终止。

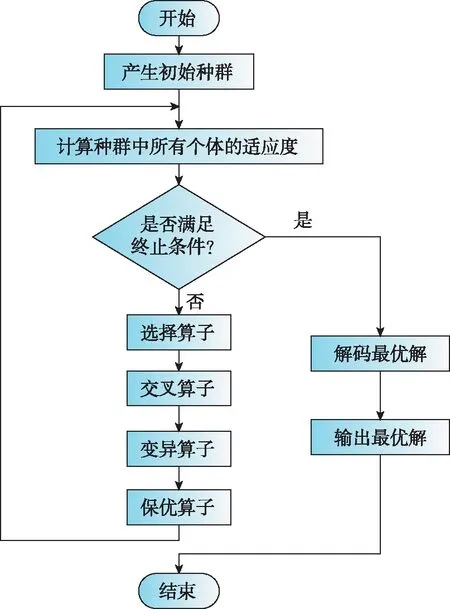
图8 遗传算法流程图Fig.8 Flowchart of genetic algorithm

2.3 优化结果

为验证算法的正确性和有效性，本文运用MATLAB软件对所提出的算法进行了仿真。对2.1节的星座中的8个待优化参数进行优化求解，结果如表6所示。

表6 遗传算法优化结果

2.1节四星原始方案相对相位为0-180-0-180，遗传算法优化后的方案为0-180-90-270。从图9的遗传算法优化过程发现，适应度函数逐代提升。优化前，5天可提供约392894.850秒时长的通信时间，可通信时间占比90.948%;优化后，5天可提供约428721s的通信时长，可通信时间占比99.24%，且间隔次数较少。图10为1天6圈回归四星组网优化前后的效能对比。可得出结论：两轨道面升交点赤经差180°较为合适，相对相位0-180-90-270比原始设计0-180-0-180要优。

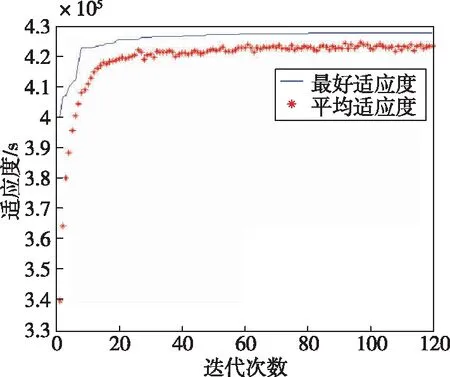
图9 迭代过程适应度变化曲线Fig.9 Fitness curve of iteration process

(a) 优化前通信时间图

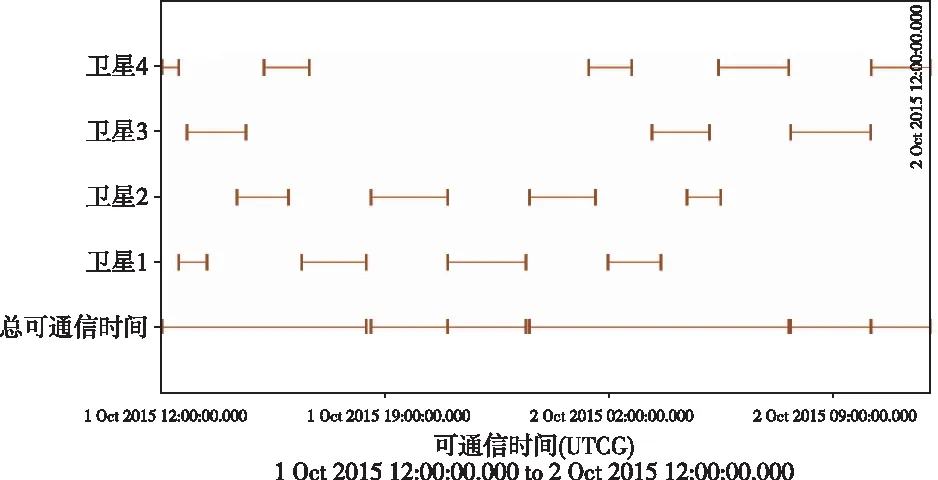
(b) 优化后通信时间图 图10 优化前后通信时间对比Fig.10 Comparison of communication time before and after optimization

3 寻找实时通信星座

按照前述遗传算法优化得到的结论，拟采用相对相位0-180-90-270的四星组网方案；通过提高轨道高度的方法，选用表1中第二行的轨道参数方案，可增加通信时间。

3.1 轨道及星座参数

卫星标称轨道设计为：

轨道半长轴：a=13517.69324 km

近地点高度：hp=658 km

远地点高度：ha=13621.1 km

最大作用距离：18954.92939 km

轨道倾角：i=63.43°

偏心率：e= 0.479487

近地点幅角：ω= 270°

轨道平周期：T=260.68354 min

回归周期：2 天

回归总圈数：11

按照遗传算法优化后的结论，即180°的升交点赤经差和0-180-90-270的相对相位方案，配置2个轨道面，每个轨道面的参数及卫星数量见表7，四星组网示意见图11。

表7 实时通信星座配置方案

图11 实时通信星座配置Fig.11 Real-time communication constellation configuration

3.2 星座效能

仿真了5天的通信情况如图12所示，结果表明可为目标区域提供24小时实时通信服务。

图12 实时通信星座可通信时间Fig.12 Communication time of Real-time communication constellation

4 结 论

本文介绍了国外战术卫星的发展情况、目标区域实时通信的实现方法、卫星星座与轨道设计优化方案，对类似任务卫星轨道与星座设计具有一定的借鉴意义。通过改进的遗传算法对轨道六根数中的升交点赤经、相位两个参数，共8个变量进行了寻优计算。经多次独立优化过程验证，证明了优化结果是一种较优的设计方案；基于此进一步通过轨道高度提高增加覆盖能力，寻找到了可实时覆盖的星座设计，满足目标区域实时通信的要求。