三轴陀螺稳定平台伺服回路全姿态解耦及变增益控制方法*

魏宗康,徐白描

(北京航天控制仪器研究所·北京·100854)

0 引 言

三轴稳定平台系统由台体、内框架、外框架和基座组成，相对于捷联系统的优点在于通过框架隔离载体的角运动，使平台台体相对于惯性空间始终保持稳定，为导航解算用的加速度计提供一个良好的工作环境。现有的文献[1-2]认为，台体相对惯性空间稳定的三轴平台存在“框架锁定”现象，即内框架角为90°时平台台体轴和外框架轴相重合从而使平台失去一个自由度。在发生框架锁定时，如果平台基座沿垂直于台体轴和外框架轴的第三个正交轴存在转动时，则通过平台外框架轴和内框架轴的轴承约束，将带动整个台体绕该第三个正交轴转动从而使其不能相对惯性空间保持稳定。为此，三轴平台在工程应用中在内框架轴上增加限位挡钉以避免内框架角工作于大角度，这就使得三轴平台只能应用于机动姿态有限的载体上。

但随着飞机、运载火箭和弹道式导弹对机动变轨飞行需求的增加，要求惯性平台在全姿态、大机动运动时台体仍能保持稳定。为此，在原来两框架三轴平台的基础上，通过在最外面增加一个随动框架构成四轴平台用来避免“框架锁定”现象的发生。为了使四轴平台的内框架工作于0°，文献[3-4]提出了一种全方位四轴平台随动回路方案。当外框架角为±90°时，可通过将随动框架转动90°的方法使内框架角回零，同时使外框架离开±90°位置，使四轴平台重新具备闭合随动回路的工作条件。这就带来一个新的问题是，既然内框架角始终工作于0°，那么四轴平台就退化为一个由台体轴、外框架轴和随动框架轴构成的三轴平台了，是不是三轴平台也能实现全姿态、大机动状态下的工作？

国内对三轴平台内框架限幅的主要依据是参考文献[1]，所建立的三轴平台运动模型中包含了内框架角的正切函数和正割函数，转动惯量和力矩变换的计算公式中也包含了内框架角度的正切值或正割值，因此当内框架角度为±90°时，计算的结果趋于无穷大，但该结论不符合物理规律。因此，本文建立了一种新的三轴平台动力学方程、伺服回路模型，并提出了一种适应全姿态的解耦方法，可对回路中的力矩耦合和转动惯量耦合进行解耦，实现了三条回路的独立控制。针对伺服回路系统中的变参数问题，本文提出了变增益控制策略，仿真结果表明该控制方法可保证伺服回路性能不变，具有更好的鲁棒性。

1 三轴陀螺稳定平台的框架系统动力学方程

包含台体、内框架、外框架和基座的三轴平台结构如图1所示，设βzk为内框架相对台体的转动角度，βyk为外框架相对内框架的转动角度，βxk为基座相对外框架的转动角度。在βzk=0、βyk=0、βxk=0时，台体坐标系OXpYpZp、内框架坐标系OXp1Yp1Zp1、外框架坐标系OXp2Yp2Zp2和基座坐标系OX1Y1Z1重合。此时，平台框架可以隔离基座的角运动，台体相对惯性空间稳定。

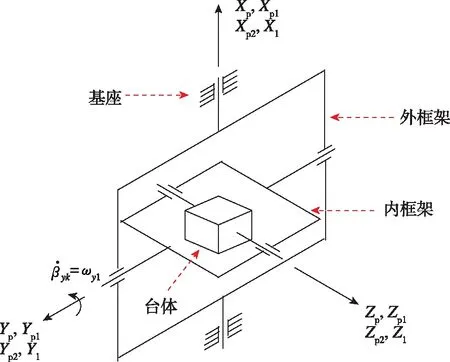
图1 框架归零时的三轴平台结构Fig.1 Three axes platform structure when frame angle values are zeros

图2 三轴平台4个坐标系之间的关系Fig.2 The relation within four coordinates of three axes platform

在建立平台系统的动力学方程时，定义ωxp、ωyp、ωzp分别为台体坐标系相对于惯性坐标系的转动角速度在Xp、Yp、Zp轴上的投影分量；ωxp1、ωyp1、ωzp1分别为内框架坐标系相对于惯性坐标系的转动角速度在Xp1、Yp1、Zp1轴上的投影分量；ωxp2、ωyp2、ωzp2分别为外框架坐标系相对于惯性坐标系的转动角速度在Xp2、Yp2、Zp2轴上的投影分量；ωx1、ωy1、ωz1分别为载体坐标系相对于惯性坐标系的转动角速度在X1、Y1、Z1轴上的投影分量。

采用欧拉法分别列写出台体、内框架和外框架的动力学方程。

(1) 台体的动力学方程：

(1)

式中，Jxp、Jyp、Jzp为台体(包括陀螺仪壳体)对Xp、Yp、Zp轴的转动惯量；Mxp、Myp、Mzp为台体Xp、Yp、Zp轴上的外力矩；MDzp为台体轴力矩电机的反馈力矩。

(2) 内框架的动力学方程：

(2)

式中，Jxp1、Jyp1、Jzp1为内框架对Xp1、Yp1、Zp1轴的转动惯量；Mxp1、Myp1、Mzp1分别为内框架轴上的外力矩，不包括电机力矩的反馈力矩；MDy1为内框架轴力矩电机反馈力矩。

(3) 外框架的动力学方程为：

(3)

式中，Jxp2、Jyp2、Jzp2为内框架对Xp2、Yp2、Zp2轴的转动惯量；Mxp2、Myp2、Mzp2分别为外框架轴上的外力矩，不包括电机力矩的反馈力矩；MDx2外框架轴力矩电机反馈力矩。

(4) 基座随着载体运动时对外框架施加的力矩为

(4)

式中，Mx1、My1、Mz1为基座受到载体的作用力矩。

2 存在奇异值的三轴平台台体合成动力学方程

式(1)～(4)是分析平台系统运动规律的基础，对其求解可得三轴平台的台体三轴动力学方程。在具体求解过程中，忽略二阶惯性干扰力矩，可以列写出各框架力矩作用到台体三个轴Xp、Yp、Zp的动力学方程。根据参考文献[1]的推导思路，依据内框架动力学方程，有

(5)

(6)

以及外框架OXp2轴动力学方程

Mxp1=

(7)

需要注意，当βyk=90°时，上式中的1/cosβyk将趋于无穷大，βyk为奇异值。把式(6)代入式(7)，再把式(7)代入式(5)，并把式(5)代入式(1)，即可求得三轴稳定惯性平台系统的台体合成动力学方程为

(8)

其中，

Jzp1cos2βzktan2βyk+Jxp2cos2βzksec2βyk；

Jzp1sin2βzktan2βyk+Jxp2sin2βzksec2βyk；

Jxp2sec2βyk)sin2βzk。

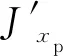
根据该动力学方程，三轴平台伺服回路如图3所示。图中，由框架至台体的干扰力矩的耦合矩阵为

(9)

在现有平台系统中只采用了平面坐标分解器进行力矩解耦，平面分解器的表达式为

(10)

但上述结果存在以下问题：

(1) 当βyk趋于±90°时，如果外框架Xp2、台体Zp轴上存在有限力矩Mxp2和Mzp，台体Xp和Yp轴将接收到趋于无限大的被动力矩。从物理意义上来说，在框架轴输入有限能量时将在台体产生无限能量，显然不符合客观规律。

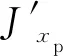
分析错误的原因，根源在于两个方面，其一是式(6)中把内框架Mzp1用台体轴力矩Mzp-MDzp表示，即该方法认为内框架的干扰力矩是由台体的运动造成的；其二是式(7)，在求解Mxp1时只用到外框架OXp2轴的动力学方程，而没有用到OZp2轴的动力学方程。

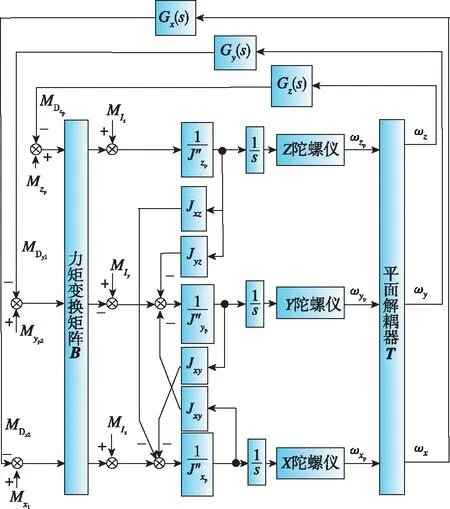
图3 基于平面坐标分解器的三轴平台伺服回路Fig.3 Three axes platform servo based on plane coordinate resolver

3 适应全姿态的三轴平台系统台体合成动力学方程

通过把内框架力矩Mzp1用外框架力矩Mxp2和Mzp2的合成来表示，采用表达式

Mzp1=[M7-(Mxp2-MDx2)]sinβyk- (M9-Mzp2)cosβyk

(11)

把上式代入式(7)，有

Mxp1=-[M7-(Mxp2-MDx2)]cosβyk-

(M9-Mzp2)sinβyk

(12)

忽略二阶小量，具体推导过程见图4。

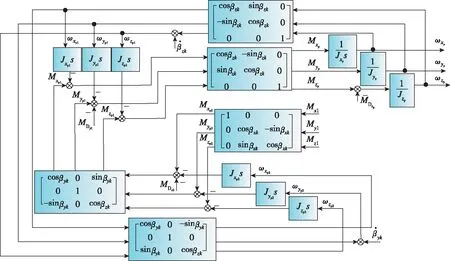
图4 三轴平台动力学方程推导流程Fig.4 Derivation flow of kinematic equation of three axes platform

(13)

其中，

4 三轴平台系统伺服回路全姿态解耦设计

在惯性稳定平台伺服系统工作时，作为伺服回路执行机构的三个力矩电机分别装在台体轴、内框架轴和外框架轴上，在不同框架角时伺服回路会存在着力矩耦合。框架系统的转动惯量最终通过惯性干扰力矩对台体的作用体现出来，包括转动惯量间的耦合、惯量积的耦合等，但最关键的是框架转动惯量在台体上的耦合。为此，在设计三轴惯性稳定平台系统的伺服回路控制器时，需要进行解耦。

目前的三轴平台的内框架角工作范围较小，一般不会超过±40°的范围，所以对伺服回路进行解耦时只考虑了力矩解耦，即所谓的坐标分解器。随着内框架角工作范围达到±180°时，转动惯量耦合对伺服回路的影响不可忽略，主要表现为两个方面：(1)三个回路交链的耦合作用会直接影响静态精度和动态精度；(2)三个回路增益大小的变化会影响相位裕度。这些都会影响平台台体相对惯性空间的稳定性和精度。为此，本文提出了一种新的三轴稳定平台系统伺服回路解耦方法，如图5所示。图中，由框架至台体的干扰力矩的耦合矩阵为

(14)

(15)

(16)

图5 基于转动惯量和力矩解耦的三轴平台伺服回路Fig.5 Three axes platform servo based on moment of inertia and moment decoupling

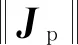
图6 解耦后的X轴平台伺服回路Fig.6 Decoupled servo loop of X-axis platform

5 三轴平台系统伺服回路变增益控制设计

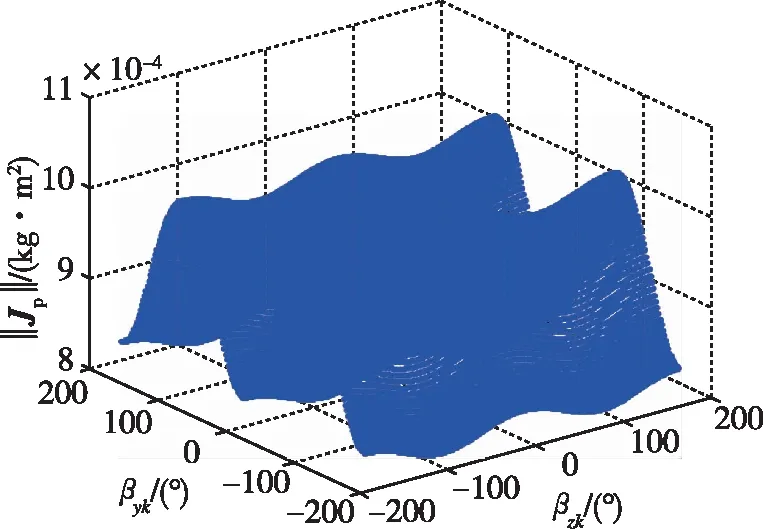
图在不同框架角时的值Fig.7 The value of according to different frame angle

本文提出一种三轴惯性稳定平台系统伺服回路变增益控制方法，实现步骤如下：

(1)根据台体上安装的陀螺仪输出的角速度，得到台体在Xp轴、Yp轴和Zp轴上的角速度分量ωxp、ωyp、ωzp；

(2)经过解耦后，得到台体Zp轴的合成转动角速度βz、内框架Yp1轴的合成转动角速度βy；外框架Xp2轴的合成转动角速度βx；

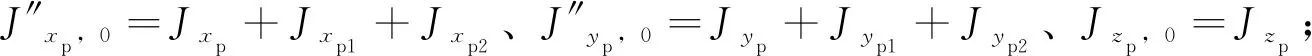
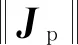
性能指标要求包括静态精度指标、动态精度指标和对象不确定性指标：(1)静态精度指标为伺服回路为一个II型系统，因此，需增加一个积分环节；(2)动态精度主要考虑在低频段尽量增加伺服回路的力矩刚度；(3)对象不确定性主要考虑高频未建模特性。由于精度指标和对象不确定性指标是一对矛盾量，因此，在设计控制器时需要在上述两个指标之间取折中[7-8]。

在具体设计时，以X轴伺服回路为例，采用H∞控制设计的βyk=0°、βzk=0°时的控制器为[11-12]

Cx,0(s)=

(19)

伺服回路开环传递函数如图8所示，可以看出，在带宽范围内的低频段，开环传递函数幅值大于性能界函数的值，而在带宽范围外的高频段，开环传递函数幅值小于对象不确定性的值；伺服回路的带宽为163.2(rad/s)，相位裕度为53.9°，满足设计要求。

图8 X轴伺服回路开环伯德图Fig.8 The magnitude versus phase plot of X-axes servo loop

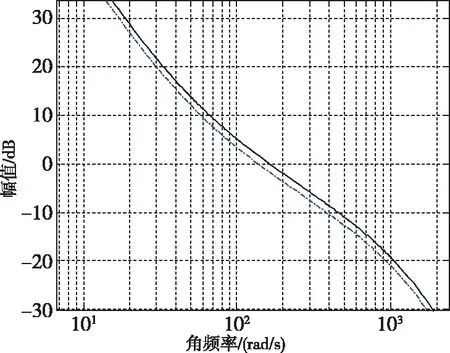
图9 X轴伺服回路开环幅值伯德图Fig.9 The magnitude plot of X-axes servo loop

为比较变增益的效果，不考虑系统中的饱和特性，设框架角βyk=90°、βzk=0°，外框架受到一个常值干扰力矩Mx1=1(N·m)的作用，电机力矩MDx2的响应过程见图10中的上图，控制器输出ux的电流见图10中的下图。无增益补偿时的伺服回路单位阶跃响应如图10中红线所示，黑线为采用变增益控制的伺服回路单位阶跃响应，可以看出，变增益控制具有响应时间快、超调量小、精度高的优点。

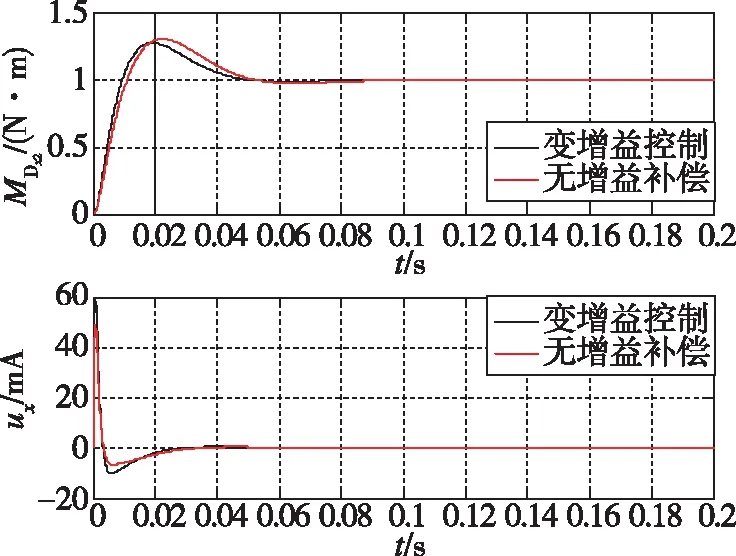
图10 X轴伺服回路单位阶跃响应Fig.10 The step response plot of X-axes servo loop

6 结 论

本文针对载体全姿态、大机动运动的应用需求，探讨了三轴平台在台体相对于惯性空间稳定时的全姿态伺服控制方法，有如下结论：

(1) 传统上认为三轴平台存在“框架锁定”而不能实现全姿态功能的观点是有局限性的，主要原因为理论推导有不足之处，在工程实际中又采用限位挡钉使内框架角工作于小角度等具体措施；本文建立了新的三轴平台伺服回路动力学模型，实现了三轴平台任意框架角时的全姿态运动描述。

(2)工程实现中三轴平台采用平面坐标分解器实现伺服回路解耦有其局限性，解耦的条件是假设内框架角工作于小角度；本文提出了一种新的伺服回路解耦方法，不仅可实现全姿态条件下框架力矩耦合的解耦，还可实现转动惯量耦合的解耦，实现了真正物理意义上的解耦。

(3) 现有的伺服回路控制器为固定参数超前滞后频率域控制器，具有较好的鲁棒稳定性，但在全姿态条件下个别性能会下降；本文提出了一种变增益控制方法，实时补偿伺服回路在不同框架角时的增益变化，确保了伺服回路的性能不变。