基于线性重力差模型的拦截弹中制导技术*
陆 诚,崔朗福,张庆振,曾浩然,聂 华,赵友铖
(1.北京航空航天大学 自动化科学与电气工程学院·北京·100083; 2.中国舰船研究设计中心·武汉·430064; 3.北京机电工程总体研究所·北京·100854)
0 引 言
机载动能拦截弹是一种由载机携带发射,在大气层内通过初始上升段进行快速爬升、大气层外中制导段缩小弹目距离、动能杀伤武器(Kinetic Kill Vehicle,KKV)末制导阶段对姿态位置进行微调并最终通过直接碰撞,实现对数千千米外的空间目标进行打击的拦截武器[1]。大气层内的初始上升段经过一、二级助推使得拦截弹在最短时间内爬升到大气层外进入中制导阶段;大气层外中制导段的主要目的是将弹目相对距离尽量减小到量级较小的值,为末制导创造良好条件[2];末制导经过初始上升段、中制导段助推后距离目标已经较为接近,通过拦截弹的最后一级KKV自带的姿轨控发动机对自身状态进行微调,使得KKV导引头能够探测到空间目标并实现直接对撞打击。其中,中制导段的任务是将数量级在上千千米的弹目距离通过中制导段尽量减小到几千米甚至几百米的数量级,对于拦截弹的成功打击具有重要作用[3]。
针对上述中制导问题的研究,陆亚东等[4]利用预测命中点的制导方法给出了发动机的定向策略,但计算量大不适合在线处理而且未考虑中制导段轨道修正后对末制导段攻击角的影响,存在不完善之处;臧月进等[5]利用零重力差模型结合最优控制和庞特里亚金极小值设计出了一种大气层外最优拦截制导律,但零重力差模型只适用于弹目距离较小的情况,当弹目距离较大时误差过大;Zes D等[6]提出了一种考虑地球重力项摄动和完整引力差的比例导引方法,通过假设弹目重力差为零来计算零控脱靶量,同样只适用于弹目初始位置较为接近、初始零控脱靶量较小的情况。
本文提出了一种通过线性重力差模型来计算脱靶时刻和零控脱靶量的方法,并基于此设计了拦截器助推级的点火策略,经过仿真验证表明本文方法能够有效应对长程(大于3000km)拦截任务,具有一定的工程价值。
1 拦截弹目标运动模型
拦截任务主要关注拦截弹与目标在惯性空间下的相对运动情况,因此在发射惯性坐标系下建立运动方程进行研究。大气层外空气稀薄,气动力可忽略不计,拦截弹与目标的质点运动方程表示如下[7]:
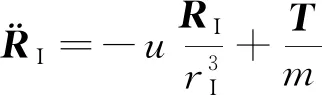
(1)
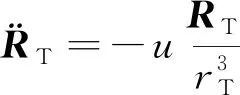
(2)
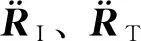
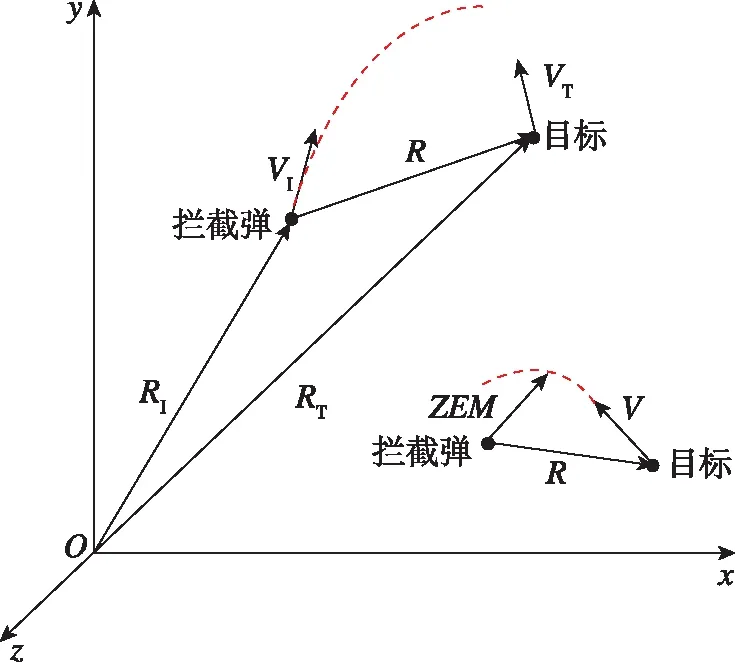
图1 空间惯性坐标系下拦截弹与目标运动情况Fig.1 Motion of Interceptor and Target in Space Inertial Coordinate System
其中拦截弹除了受到引力作用之外还受到额外的推力T作用,零控脱靶量是指从当前时刻起,不加外部控制、只受引力作用下拦截弹与目标最终的位置矢量偏差,既可以作为一种衡量拦截器全段制导精度的性能指标,也可以作为对当前状态进行指引的预测值。当前状态下弹目相对运动方程如下[8]:
(3)
拦截弹多段助推的目的是通过调整推力矢量使得弹目相对距离最小,也就是实现对目标的拦截。上述非线性二阶时变方程难以通过实时解析方法得到精确解,而整个中制导段的目的就是通过调节T推力的大小和方向,将二者位置矢量差值尽可能降低,因此对于公式(3)中二者重力差值ΔG(t),提出四种模型进行简化处理,提高零控脱靶量预测值的计算速度。
2 四种重力差模型的建立
分别提出等重力差、常值重力差、线性重力差、二次重力差四种模型[9],给出相应的解析式并求出各自对应模型下的零控脱靶量预测值。
2.1 等重力差模型
假设拦截弹与目标所受重力相等[9],公式(3)简化为:
(4)
在外部推力作用T=0时,相对运动方程如下:
(5)
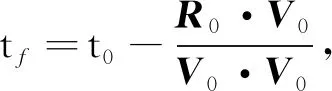
(6)
2.2 常值重力差模型
拦截弹与目标初始时刻重力差值ΔG(t0)可以通过指挥控制通信系统(Command and Control Integrated Communication and Intelligence System,C3I)和拦截弹自带导航系统得到,而最终脱靶时刻可认为弹目位置较为接近,重力差ΔG(tf)=0,因此常值重力差为两个端点平均值[9],即:
(7)
常值重力差模型下相对运动方程如下:
(8)
结合零控脱靶量的定义并利用牛顿迭代法求解出拦截时间tf,带入可得常值重力差模型下的零控脱靶量预测值:
(9)
2.3 线性重力差模型
线性重力差模型即假设自由飞行段飞行器所受重力(地球引力)随时间线性变化[9],即:
(10)
此时相对运动方程形式如下:
(11)
求解零控脱靶量预测值细节不再赘述,直接给出结果:
(12)
2.4 二次重力差模型
进一步对重力差模型进行精确模拟可假设重力差值以二次函数形式变化[9]。为获得二次函数模型需要知道两个时间点t0与tp时刻导弹与目标的重力差。二次重力差模型可表达为:
ΔG(t)=ΔG2(tp,t0,tf)(tf-t)2+
ΔG1(tp,t0,tf)(tf-t)
(13)
此时的相对运动方程如下:
(14)
求解出二次重力差模型下的零控脱靶量预测值:
V(t0)(tf-t0)+R0
(15)
在此基础上对上述四种重力差模型精度进行分析:以助推火箭中制导段终端时刻t0作为初始条件,分别采用上述四种零控脱靶量预测模型进行仿真,拦截目标为800km的赤道圆轨道空间目标,拦截器与目标在t0时刻状态如下表:

表1 弹目初始状态
得到的四种模型下实际轨道和预测轨道偏差情况如下所示:
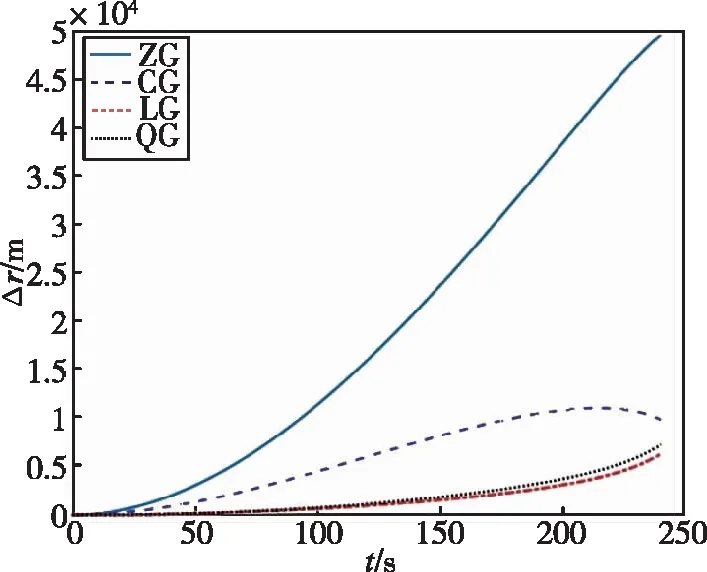
图2 弹道预测精度对比Fig.2 Precision comparison of trajectory prediction
表2 脱靶时刻预测精度对比
Tab.2 Precision comparison of miss time prediction
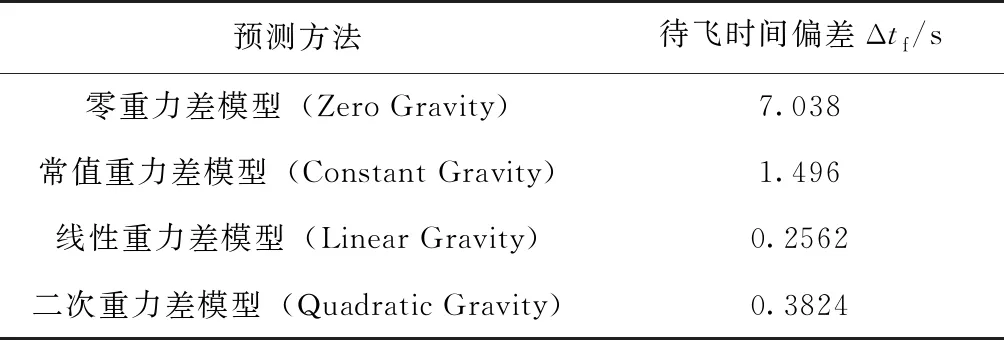
预测方法待飞时间偏差Δtf/s零重力差模型(Zero Gravity)7.038常值重力差模型(Constant Gravity)1.496 线性重力差模型(Linear Gravity)0.2562二次重力差模型(Quadratic Gravity)0.3824
由仿真结果可见线性重力差模型与二次重力差模型的预测值与真实值偏差量较小,由于二次重力差模型需要更多参数,但在精度上没有很大优势,因此选择线性重力差模型预测零控脱靶量。
3 中制导律设计
通过前文分析,可以得到较为精确的零控脱靶量预测值ZEMpred,基于求得拦截弹推力矢量T=Tλ(T为拦截弹推力大小,λ为推力方向的单位矢量)将零控脱靶量预测值ZEMpred消除为零[10]。
制导律具体形式如下:
T=TλΛ=ε+KZEM⊥=Λλ
(16)
表示为两项之和:第一项ε=R/R为弹目视线方向上的单位向量;第二项KZEM⊥为零控脱靶量垂直于弹目视线方向上的分量ZEM⊥与增益K的乘积。二者有如下关系:
(3)原虫寄生类疾病。在对这类疾病进行治疗时,因为大部分抗寄生虫药物都含有一定毒性,为将这些药物的副作用降低到最小,防疫人员在用药的同时应通过营养、强心等药物升治疗效果。
ZEM⊥=ZEM-(ZEM·ε)ε
(17)
因此推力方向主要由零控脱靶量在弹目视线方向和垂直于弹目视线方向的两个分量决定,实际应用当中主要通过调节增益系数K来对两个分量进行调整。
中制导过程中,拦截弹与目标的相对运动方程如下:
(18)
其中ε,n分别为沿弹目视线方向上的和垂直于弹目视线方向上的单位矢量,结合制导律公式可得:
(19)
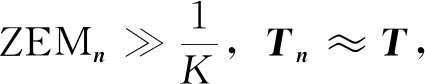
4 拦截器助推级点火时间确定
前述方法可以得到精度较高的零控脱靶量预测值ZEMpred,并通过制导律设计可以使ZEMpred趋近于零,但一方面预测值与真实值存在一定的偏差,另一方面随着中制导段无控飞行时间的增长,原本趋近于零的ZEMpred可能会出现发散,因此如果不加以限制,很有可能出现脱靶。
为解决可能出现的脱靶问题,采用延迟中制导二次助推(也即拦截器助推级)点火的策略,因此将助推级的作用更多地体现在中制导段的轨道修正上[11],因此拦截弹二级助推完成后先进行一段时间的自由飞行,并通过实时参数计算得到某一点火信号Jk,满足开机条件之后开启拦截器助推级来修正零控脱靶量的预测值ZEMpred。
选取开启时间主要有以下原则:
(1)末制导段KKV轨道修正能力有限,为提高打击精度不能过晚开启助推级;而助推级完成助推之后已经修正为零的零控脱靶量预测值ZEMpred可能会再次发散,因此助推级也不能开启过早[12]。
确定以上原则后若信号不满足开机条件则拦截弹继续飞行直至满足;若一直不满足条件则实时计算待飞时间dt=tf-t=100s时开启拦截器助推级[13]。
结合地面测试得到的拦截器速度增量ΔV和实时待飞时间tf可决定拦截器变轨能力ΔR:
(20)
其中twork为拦截器助推级的工作时间,可见飞行过程中变轨能力ΔR在不断变小,若变轨量ΔR小于零控脱靶量预测值ZEMpred则在理论上无法命中目标;结合实际情况下计算待飞时间要考虑助推级的加速过程以及推力方向的限制,定义点火信号如下:
(21)
其中0≤M≤1为一常数,一般选取0.6~0.8之间。定义Jp=Jc/ΔR,其中Jc是零控脱靶量的绝对值,因此Jp表示拦截过程中的需求和剩余实际变轨能力的比值;点火信号为上升沿触发[12],第一次由0置1时拦截器助推级点火。
至此,中制导律设计部分完成。
5 仿真验证
5.1 中制导仿真验证
根据上文设计的中制导律,在Matlab Simu-link环境下进行仿真,目标为1000km高的赤道圆轨空间目标,弹目初始状态如下,中制导段二级助推火箭剩余工作时间为30s,拦截器主推机工作时间为60s,弹目初始距离为3596.3km。

表3 弹目初始状态
中制导段仿真结果如下:
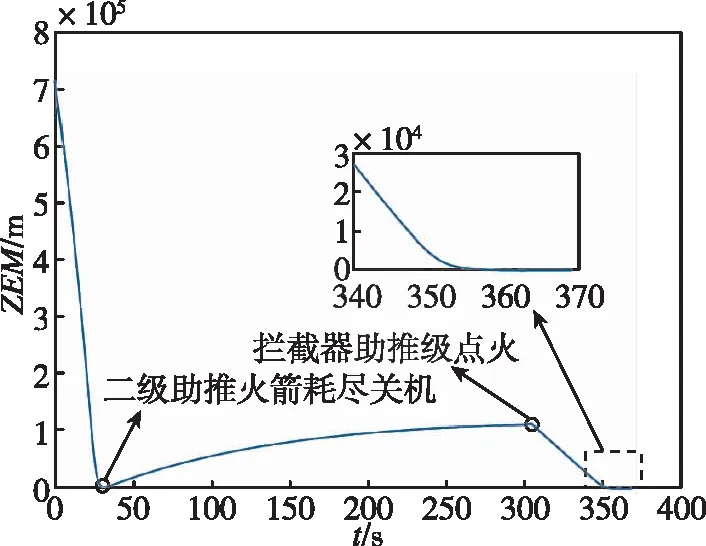
图3 零控脱靶量预测值ZEMpred与时间关系Fig.3 The relationship between predicted zero miss distance and time
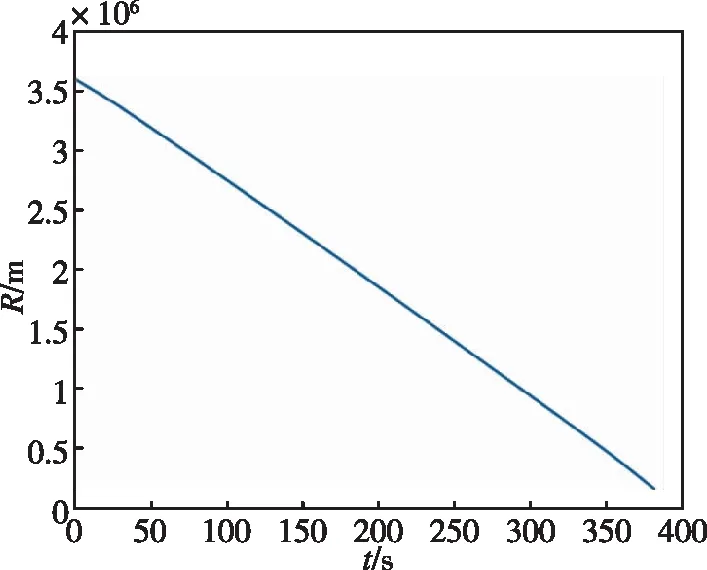
图4 相对距离与时间关系Fig.4 The relationship between relative distance and time
中制导段仿真结果可知:
(1)二级助推火箭关机时减小为零的零控脱靶量预测值ZEMpred逐渐发散;在长距离自由飞行后由302.34s开启拦截器助推级,将零控脱靶量预测值ZEMpred再次修正为零。
(2)弹目相对距离始终呈减小趋势,最终脱靶量为164.51m,也就是说末制导段KKV只需要修正164.51m的脱靶量即可。
5.2 全段仿真验证
结合拦截弹全段对中制导律进行验证,为简化问题给出如下假设:(1)只考虑相对惯性系位置,不考虑地面相对位置;(2)轨道为圆形轨道;(3)目标从北向南看逆时针运动。
5.2.1 仿真情况一
目标为800km轨道高度的圆轨道空间目标,弹目初始条件如表4所示。
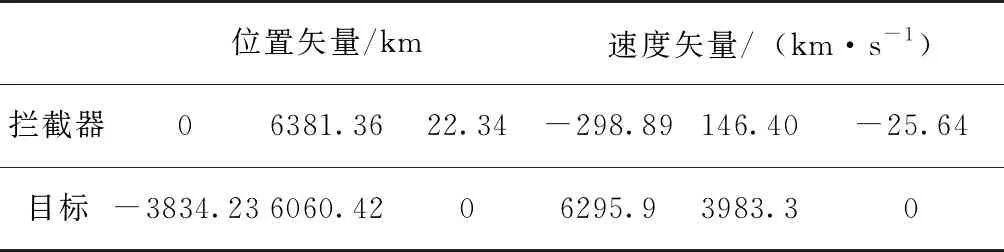
表4 弹目初始状态
全段仿真结果如下:
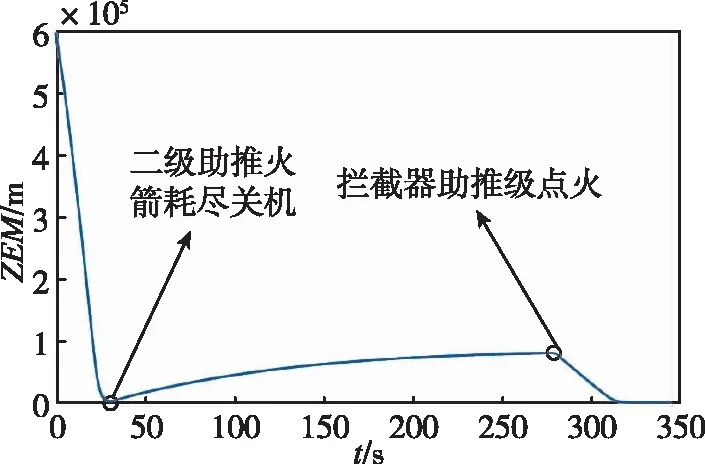
图5 零控脱靶量在中制导段随时间变化Fig.5 The relationship between zero miss distance and time in midcourse
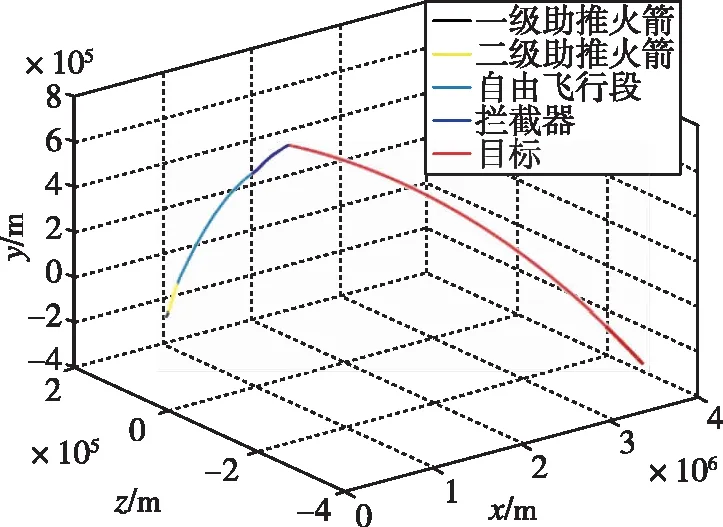
图6 发射坐标系下全段弹道仿真Fig.6 Simulation of whole trajectory in launch coordinate system
拦截过程中的全段参数如下表所示:
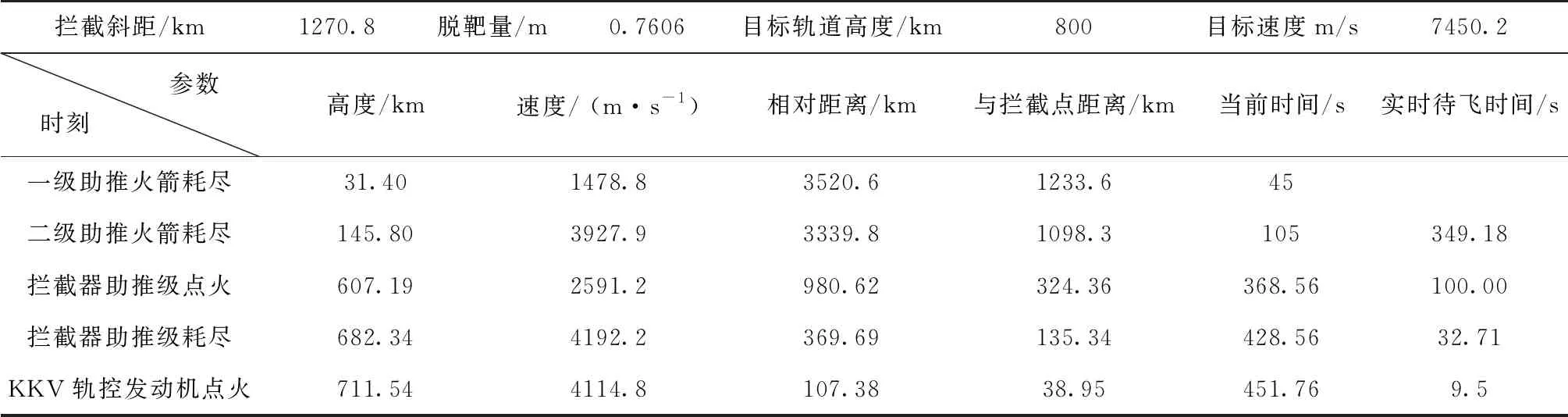
表5 全段弹道仿真参数
从仿真结果可以看出,最终的零控脱靶量为0.7606m,可认为全段制导律能够成功拦截800km高度的空间目标,并且助推级点火由待飞时间条件触发也即正常点火,剩余射程能覆盖脱靶量,有足够的拦截能力。
5.2.2 仿真情况二
目标为1200km轨道高度的圆轨道空间目标,弹目初始条件如下:

表6 弹目初始状态
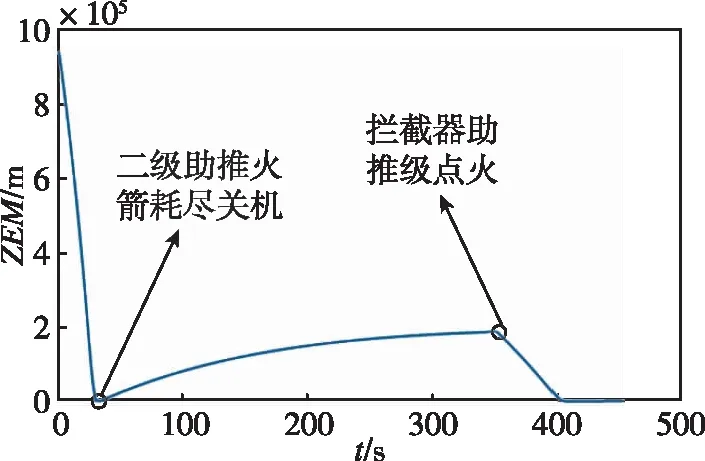
图7 零控脱靶量在中制导段随时间变化Fig.7 The relationship between zero miss distance and time in midcourse
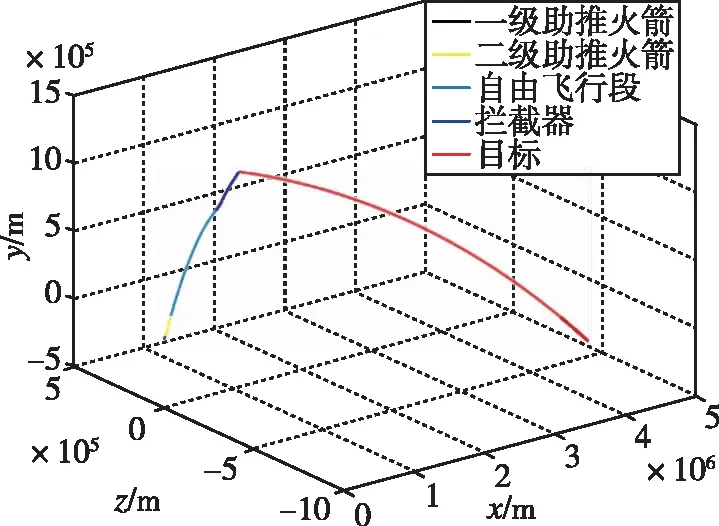
图8 发射坐标系下全段弹道仿真Fig.8 Simulation of whole trajectory in launch coordinate system
拦截过程中的全段参数如下表所示:
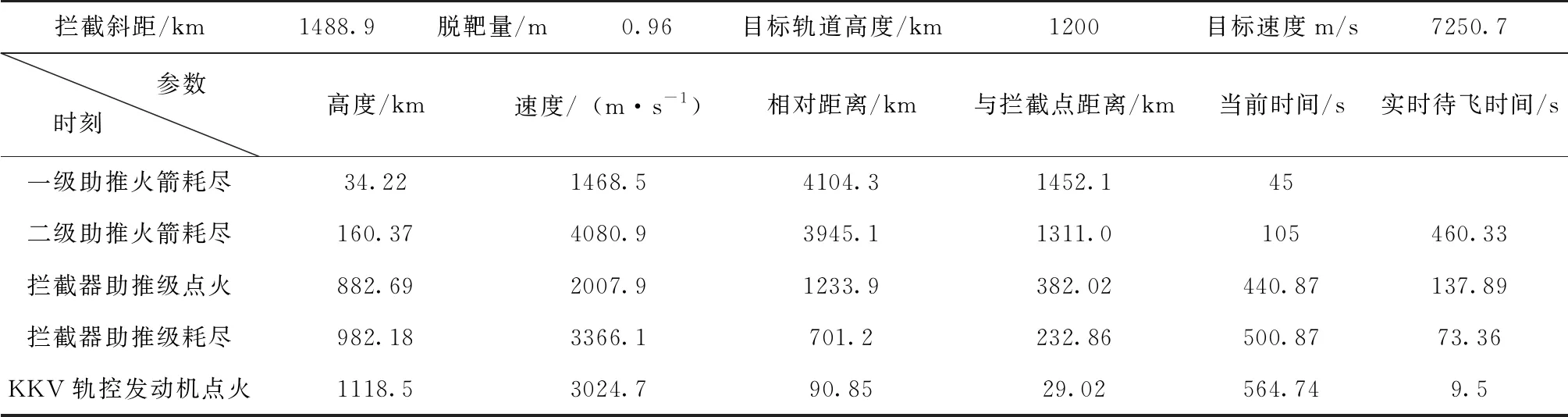
表7 全段弹道仿真参数
从仿真结果可见,最终的零控脱靶量为0.96m,可认为全段制导律能够成功拦截1200km高度的空间目标,并且拦截器助推级由轨道修正能力条件触发,也即提前点火;若仍按照待飞时间条件触发则脱靶量会在千米级别,证明点火策略对拦截情况的有效预判与控制能力。
6 结 论
本文结合机载动能拦截弹任务需求,结合多级助推各段制导的特点,选择零控脱靶量预测值作为指标设计了一种预测制导方法,随后介绍了基于四种模型的预测方法(零重力差模型、常值重力差模型、线性重力差模型、二次重力差模型),并经过仿真说明线性重力差模型较优,选取线性重力差模型预测零控脱靶量;在此基础上设计中制导律,确定制导增益;针对长距离拦截情况下的零控脱靶量预测值发散问题,采用延迟点火策略,结合实际拦截情况与自身拦截能力设计拦截器助推级点火信号。最后对所设计的中制导律与点火信号进行仿真验证,仿真结果表明制导律对于长距离拦截具有较高精度,能够为末制导提供良好的初始条件。

