基于分段常值的全电推进GEO卫星制导策略*
张 冉,李小娟,韩 潮,张亚航,于俊慧
(1.北京空间飞行器总体设计部·北京·100094; 2.北京航空航天大学 宇航学院·北京·100191)
0 引 言
电推进系统以其比冲大、推力小的技术特点在深空探测、近地轨道阻力补偿、轨道位置保持等领域得到应用[1]。近年来,电推进器在GEO轨道转移中崭露头角。欧洲先进通信卫星ARTEMIS(2001)和美国先进极高频军事通信卫星AEHF-1(2010)原计划以化学推进和电推进结合的混合方式进行GTO-GEO轨道的转移,但因不同的故障导致化学推进失效,电推进系统成为GEO轨道转移的主推力器,超时工作挽救了任务。波音公司基于702SP平台发展了全电推进通信卫星,迅速投入商业市场;截至目前,已有五颗702SP平台全电推进卫星发射入轨,单星质量在1950 kg~2300 kg之间,每颗卫星配备了4台XIPS-25离子推力器,总推力大小为165 mN,GEO入轨时间为6个月;其中两次发射采用猎鹰九号“一箭双星”的发射方式,极大降低了发射成本。空中客车防务与航天基于E3000EOR平台也发展了全电推通信卫星,单星质量3550 kg~5300 kg之间,每颗卫星配备一台SPT140D稳态等离子推力器,推力大小约290 mN,GTO-GEO轨道转移时间为4~6个月;目前已有三颗E3000EOR平台的通信卫星发射入轨。全电推进通信卫星采用比冲更高的电推进系统进行GTO-GEO的轨道转移,可以大幅减少燃料质量,有效降低卫星总重或提高有效载荷的质量比,延长任务的寿命,降低发射成本[2-4]。因此,在GTO-GEO轨道转移中采用电推进技术已经成为中小型通信卫星发展的趋势,研究电推进GEO轨道转移优化和制导方法具有重要的工程意义。
全电推进GEO卫星的轨道转移设计主要分为轨迹优化和制导控制两个方面。求解航天器轨迹优化最优控制问题的数值方法分为直接法、间接法和结合二者的混合法[5-6]。直接法通过离散变量和参数将最优控制问题转换为参数优化问题,然后通过非线性规划算法获得最优解,直接法的计算量比较大。间接法通过变分法和庞特里亚金极大值原理构造两点边值问题(Two-Point-Boundary-Value-Problem,TPBVP),然后通过打靶法求解靶函数;间接法的困难在于靶函数的收敛域很小,靶函数对于初值特别敏感。一些学者提出同伦法[7-9]和非线性滤波参数估计算法[10]等解决初值敏感的数值问题。混合法则结合了直接法和间接法各自的优点,通常假定推力结构,由间接法的必要条件保证控制的最优性。在对控制结构适当假设和简化的前提下,一些学者获得了轨迹优化的解析求解方法。Kechichian[11]提出了保持偏心率为零的前提下使半长轴和轨道倾角最快改变的分段常值控制律;田百义等[12]在小推力GEO入轨问题中假设平面内外控制解耦,平面内保持远地点高度不变,平面外在升降交点采取控制的解析策略。高扬[13]提出三种分别控制轨道半长轴、偏心率和轨道倾角的切向、惯性和偏航控制律。解析法的控制律只能达到次优的控制结果,与最优转移相比有一定差别。在小推力轨道转移制导方法研究方面,许多文献提出了跟踪最优轨迹的控制思路[14-15],通过设计一组控制参数,修正实际轨道与参考轨道之间的偏差;另外,基于李雅普诺夫函数理论的制导律也得到利用,主要问题是李雅普诺夫函数的定义方式和增益的计算[16-17]。
本文主要研究全电推进GEO卫星的入轨转移制导策略问题,提出了一种跟踪最优参考轨迹的分段常值制导策略,该策略形式简单,易于星上执行,并且控制结果与最优控制律相差不大,可为我国全电推进通信卫星平台的研究提供参考。
1 电推进GEO转移轨迹优化模型
本文采用经典轨道要素的高斯摄动方程作为轨道转移优化的控制模型,形式如下:
(1)
式中,μ为地球引力常数,a为轨道半长轴,e为轨道偏心率,i为轨道倾角,Ω为升交点赤经,ω为近地点幅角,θ为真近点角;p为轨道半通径,h为轨道角动量大小,r为卫星地心距,v为卫星速度大小;控制加速度a在卫星速度方向、垂直速度方向和动量矩方向的三个分量分别为ft,fn,fh。a是除二体加速度外的其他外力加速度矢量,包含发动机推力和摄动加速度矢量两部分;本文摄动加速度仅考虑了地球非球形引力场J2项的影响。
设卫星质量为m,全电推进发动机具有上限推力大小Tmax和常值比冲Isp,g0为赤道重力加速度,式(1)改写为矩阵的形式:
(2)

对于全电推进GEO卫星的燃料最优轨道转移问题,性能指标为
(3)
转移时间tf是相应时间最短问题转移时间tfmin的倍数,用系数Ctf表示,Ctf>1。
利用变分法和极大值原理,小推力燃料最优GEO轨道转移问题可以表述为下面的两点边值问题:
(4)
其中,λ是与轨道要素对应的协态变量,λm是与质量对应的协态变量,λθ,λΩ,λω分别是与真近点角、升交点赤经、近地点幅角对应的协态变量,Ctf是飞行时间系数;下标“0”表示初始时刻的状态,下标“f”表示变轨终止时刻的状态。
上述TPBVP问题需要利用打靶法求解协态变量的初值λ(t0)、λm(t0)。对于电推进GEO轨道的转移问题,轨道转移过程包含几百圈轨道,转移时间长达半年左右,靶函数对于初值非常敏感。为了解决数值求解困难,本文采用了文献[10]提出的UKF非线性滤波参数估计算法。
2 小推力GEO转移参考轨道
本文仿真中采取的初始轨道是GTO转移轨道,轨道要素如表1所示。飞行时间系数Ctf设为1.5,使用UKF滤波参数估计算法求解不同推力值Tmax情况下的燃料最优GEO轨道转移问题。为避免结果陷入局部极值,本文采取逐步缩小推力幅值Tmax的延拓思路,每一步计算时以上一步计算结果为初值,并根据控制结构筛查全局最优的极值。

表1 轨道转移初始与目标轨道要素
图1(a)显示了燃料最优GEO轨道转移问题不同推力幅值Tmax条件下轨道半长轴、偏心率和轨道倾角随时间的变化历程,为便于比较,横轴的时间做了去单位化处理(t=t/tf)。Tmax较大时,轨道要素的变化呈现出“阶梯”形,这是由Bang-bang控制结构造成的。随着Tmax的减小,轨道要素的变化变得平滑,局部放大后仍存在“阶梯”特性。不同Tmax条件下,轨道要素呈现出相似的变化趋势,可以考虑用一条平滑曲线去拟合轨道要素的变化规律。
第1节获得了燃料最优GEO转移的最优轨迹和最优控制曲线,这些轨道和控制信息可以作为实际工程中飞行制导的参考,然而直接存储上述轨道与控制信息有以下几个缺点:①轨道圈数多,转移时间长,存储数据量大;②最优控制律的表达式与协态变量相关,而协态变量没有其他物理意义;③状态变量和控制变量与时间关联,摄动力和控制偏差会造成相应状态在指定时间达到预定数值,使存储信息失效;④轨道要素随时间的小幅度振荡影响制导律的设计。
为解决以上问题,本文利用拟合方式获得简单解析形式的曲线,更适合在星上计算机存储和利用。根据最优轨迹的形状,本文选择简单的多次多项式对最优轨迹进行拟合,数值试验表明,采用四次及以上的多项式对最优轨迹的拟合效果比较好。
图1(b)为使用四次多项式对推力幅值Tmax为2.5 N、1.0 N、0.5 N和0.2 N条件下的燃料最优GEO轨道转移轨迹进行拟合时获得的参考轨道,四条拟合曲线非常接近。Ctf固定时,燃料最优轨道转移轨迹的轨道要素变化趋势与推力大小关系不大,在设计小推力燃料最优转移问题的参考轨道时,仅需计算较大推力条件下的轨道转移工况,通过曲线拟合方式可以快速得到小推力条件下的参考轨道。
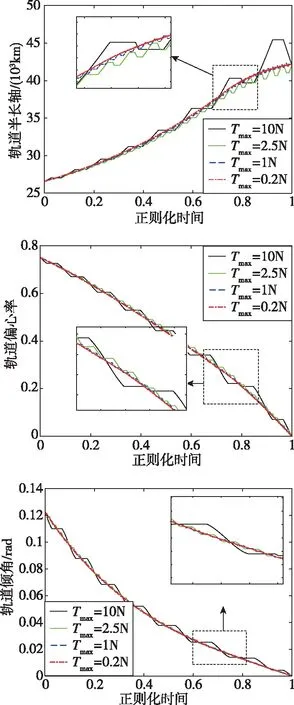
(a)最优轨迹
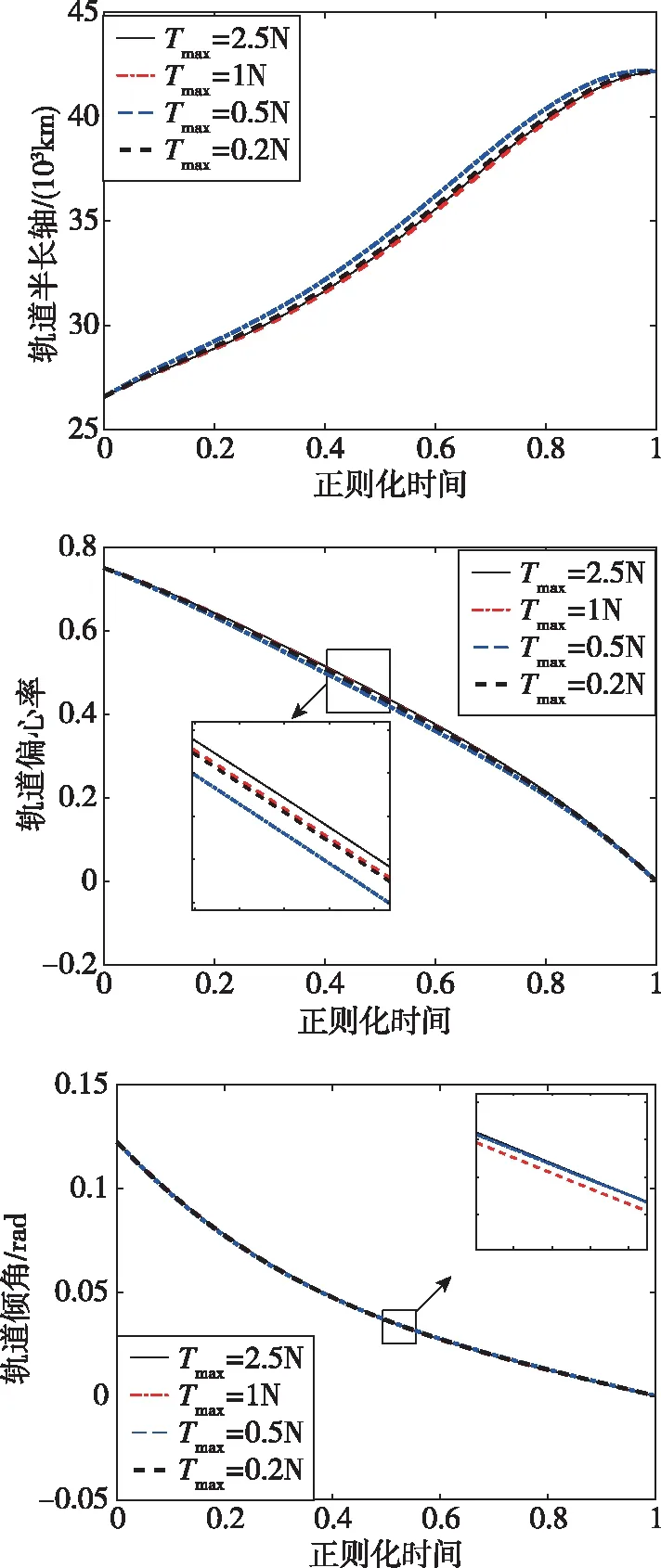
(b)拟合轨迹
3 分段常值跟踪制导策略
第一节的最优轨迹对应的最优控制是一组开环的控制,这些数据中控制力的大小和方向等数据量非常大,不适合在星上计算机存储;控制力的方向与当前协态变量和状态变量以及时间相关,协态变量本身没有具体的物理含义,这给制导律的设计带来了很多不便。在卫星的实际变轨过程中,不确定的扰动因素、未建模的摄动力、导航与控制偏差会导致卫星偏离参考轨道,必须设计含闭环反馈的制导控制律。在获得解析化的参考轨道之后,多圈长时的轨道转移问题可以分解为多个单圈转移设计问题,根据参考轨道的形式,将整个轨道改变量以一种近乎优化的方式分配到每一个轨道周期内,本节基于此基础设计单圈内的轨道制导律。
电推进控制加速度[ft,fn,fh]T与引力加速度相比是小量,使用偏近点角E代替真近点角θ作为第六个轨道要素,dE/dt可以近似为:
(5)
式中,n为轨道角速度。将式(5)代入式(1),可得到以偏近点角为独立变量的微分方程:
(6)
在推力加速度[ft,fn,fh]T作用下,卫星轨道偏近点角由E1到E2的过程中轨道要素的变化量具有解析表达式,轨道要素X的改变量具有以下形式:

(7)
根据式(7),根据不定积分的公式,可以获得TX,NX,HX的表达式,具体形式可以参考文献[18]。
卫星在偏近点角由E1到E2的过程中满推力工作时,质量的改变量为:
(8)
图2显示了燃料最优GEO轨道转移的最优控制的曲线和设计的常值推力控制结构,其中ut,un,uh是推力加速度单位矢量在速度方向、垂直速度方向和动量矩方向上的三个分量。细线表示的是最优控制曲线,黑粗实线是根据最优控制曲线形状设计的分段常值控制结构。

(a)轨道控制前中期
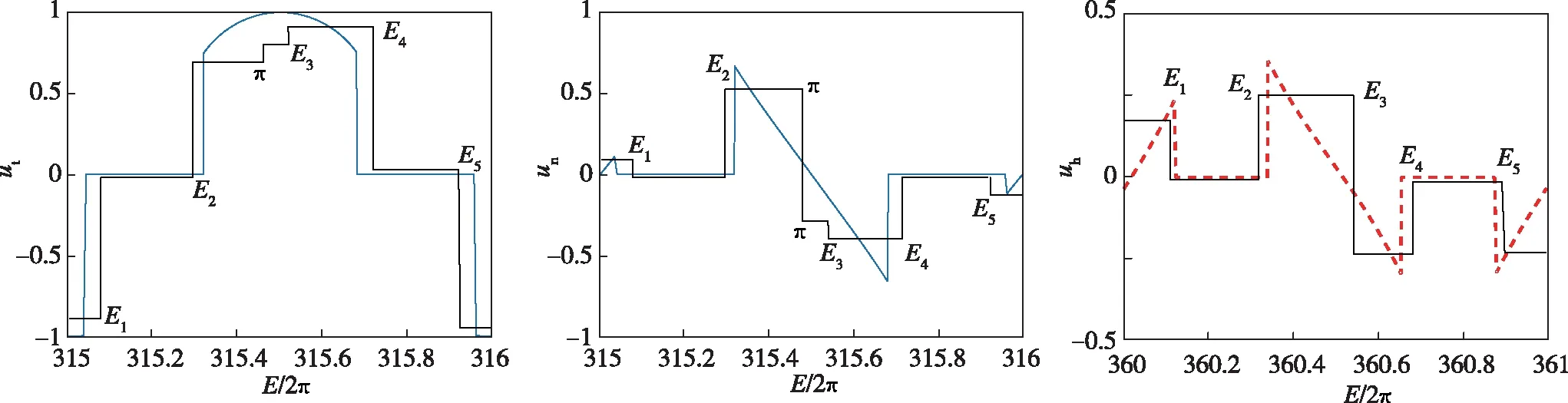
(b)轨道控制末期图2 最优和分段常值推力控制结构Fig.2 Optimal and piecewise constant thrust control structure
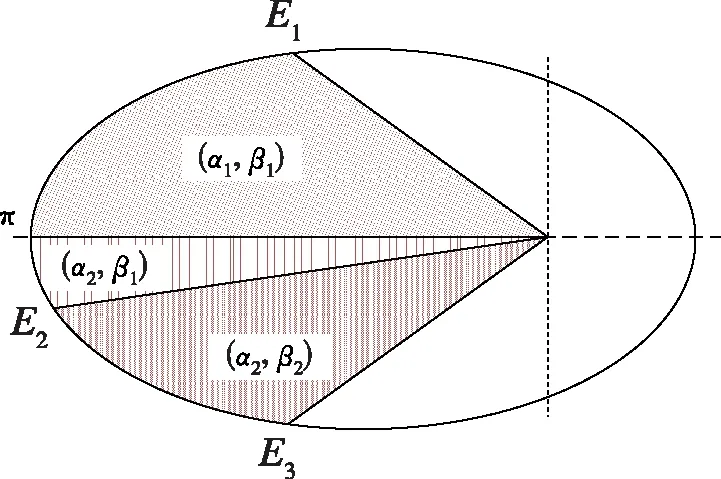
在轨道转移的前中期,平面外有两个推力弧段:[E1,E2]和[E2,E3]段,平面外推力方向分别用β1和β2描述;平面内的推力方向角用α1和α2描述。常值推力结构见表2所示,在轨道转移的前中期,每个轨道周期内,在三段常值推力的作用下,轨道要素的变化量为:

(9)
轨道转移的末期,平面外有四个推力弧段,弧段用五个设计变量描述:E1,E2,E3,E4,E5;平面内根据E3和π的大小关系,分为五个推力弧段;为减少变量数目,分别用四个方向角α1,α2,β1,β2描述推力矢量的方向,轨道转移末期的常值推力结构如表3所示。在轨道转移末期,在五段常值推力作用下,轨道要素的变化量为:
ΔX=
(10)

表3 轨道末期的常值推力弧段
在考虑J2摄动时,单圈内的控制结构如图3所示。在轨道转移的前期和中期,控制序列包含三个连续的推力弧段和一个漂移弧段,设计变量为
σ=[E1,E2,E3,α1,α2,β1,β2]
(11)
性能指标为:
J=(E3-esinE3)-(E1-esinE1)
(12)
约束条件为:

0≤α1,α2,β1≤π/2,-π/2≤β2≤π/2
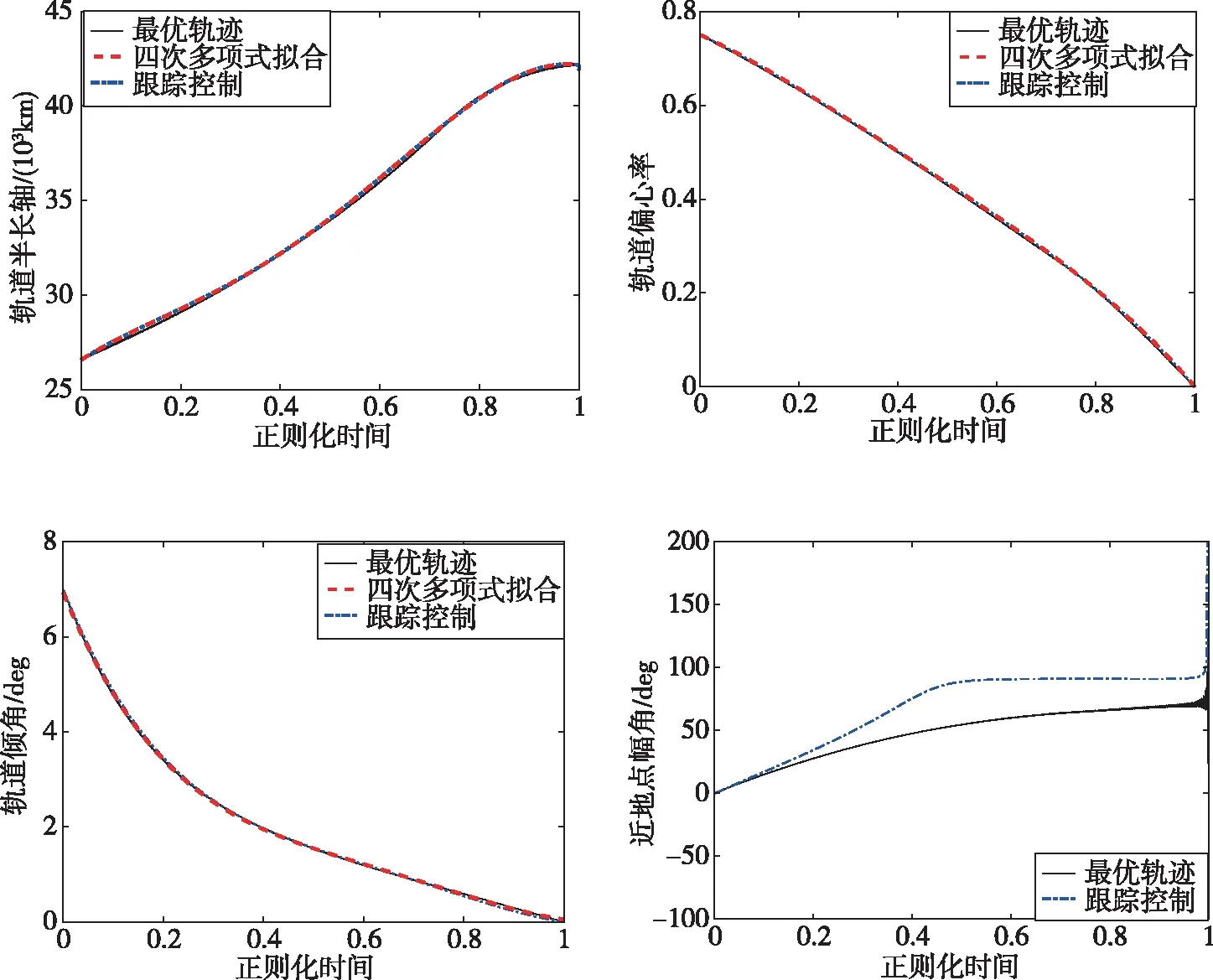
0 (13) (a)轨道控制前中期 (b)轨道控制末期图3 单圈内的控制序列示意图Fig.3 Schematic diagram of control sequence in a single loop 在轨道转移的末期,单圈内控制序列包括五个推力弧段和两个漂移弧段,设计变量为: σ=[E1,E2,E3,E4,E5,α1,α2,β1,β2] (14) 性能指标为: J=(E4-esinE4)-(E2-esinE2)+(E1-esinE1)-(E5-esinE5) (15) 约束条件为: (16) 其中ΔX为根据式(10)所计算的轨道要素改变量。 以上完成了控制单圈内数学规划问题的数学建模,这是一个具有简单边界约束的优化问题,该类问题有较成熟的优化算法;控制律充分利用了最优控制的变化规律,给出了较好的初值;每一圈的优化结果可以作为下一圈的设计变量初值,提高了优化求解速率。 选取表1所示的初末轨道要素,最大推力值为Tmax=0.2N,在最优轨迹计算时考虑J2项摄动,最优轨迹的飞行时间为265.53天,燃料消耗123.84 kg;采用四次多项式拟合生成参考轨道。图4显示了本文提出的分段常值推力跟踪制导策略的控制结果,半长轴、偏心率和轨道倾角的跟踪效果非常好。在考虑J2项摄动的情况下,变轨结束后轨道半长轴控制误差为0.83 km,偏心率误差为0.00145,轨道倾角控制误差为0.0025°。由近地点幅角的变化规律可以看出,跟踪控制并不会抑制近地点幅角ω的漂移。分段常值跟踪控制的飞行时间为266.96天,燃料消耗132.72 kg。本文提出的分段常值跟踪制导方法与最优轨迹相比,飞行时间延长0.54%,燃料消耗增加了7.17%。燃料消耗的主要原因是简化的分段常值的推力结构控制效率低于连续变化的最优控制结构。如果能根据最优控制结构的形状,找出一组简化的数学解析式来模拟推力值与偏近点角的关系,燃料消耗能够进一步优化。 图4 GTO-GEO转移分段常值制导轨迹、拟合轨迹和最优轨迹Fig.4 GTO-GEO transfer piecewise constant guidance trajectory, fitting trajectory and optimal trajectory 本文针对全电推进GEO卫星的入轨转移制导策略进行了研究分析,提出了一种跟踪参考轨道的制导策略,并结合算例分析了制导策略的效果。根据最优轨迹的变化规律,提出采用多次多项式拟合最优轨迹生成参考轨道的方法,参考轨道形式简单,能够表征最优转移轨道的变化特点,易于在星上计算机存储和使用。跟踪参考轨道的闭环反馈控制策略将多圈轨道转移的控制量分配到每一个轨道单圈内,保证了制导的燃料近优性。在轨道单圈内,本文提出一种分段常值推力控制结构,这种控制结构形式简单,在此假设下轨道要素改变量有解析解,简化了制导策略设计;并且常值推力结构易于工程实施。仿真结果显示,在考虑J2摄动条件下,分段常值的制导策略比最优控制解多消耗7.17%的燃料,对参考轨道的跟踪效果好,控制精度高。上述设计可为我国全电推进GEO通信卫星的入轨控制提供参考。为进一步提高跟踪制导策略的效率,后续可研究一类模拟最优控制结构的解析连续变化的曲线,并进一步考虑更多的工程约束条件。

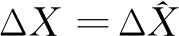
4 结 论

