基于自适应多设计融合航天器近距离操作的执行器故障补偿技术研究*

马亚杰，任 好，姜 斌

(南京航空航天大学 自动化学院·南京·211106)

0 引 言

近年来，随着空间技术的飞速发展，各国的空间活动也越来越多且空间任务的复杂性也在逐渐增加[1-2]。航天器近距离操作因其在空间探索中的实际应用受到广泛的关注[3-6]，如抓捕空间碎片、无动力航天器加油、大型航天器构造和维修服务等。航天器近距离操作包含追踪航天器和目标航天器。追踪航天器需要同时协调地跟踪目标航天器的姿态和位置。

容错性能是航天器近距离操作中的重要一环[7-10]。在实际情形中，执行器故障将会直接导致一个空间任务的失败，并引发很多潜在的问题，比如过度的燃料消耗、在轨碰撞等。如何保证当执行器故障发生时，对航天器近距离操作系统实行一个有效的并且稳定的控制已经成为一个热门的研究话题。容错控制系统能够在故障发生时补偿故障，并且将控制系统性能保持在一个可以接受的水平。但是如今大多数的文献仅仅考虑了航天器近距离跟踪控制[11-13]，或在考虑故障时，未将姿态和位置的耦合信息纳入容错控制系统中[14]。所以对于航天器近距离操作的容错控制是必要且亟需的。

本文为基于对偶四元数描述的带有执行器故障的航天器近距离操作系统设计了一个基于多设计融合的自适应故障补偿策略，其中未知故障发生在推力器和反作用轮上，不需要故障诊断，包含一个反馈控制律和对控制器参数和故障参数的自适应估计。所设计的自适应故障补偿策略可有效保证系统的稳定性和期望的跟踪性能。

1 问题描述

本节主要介绍对偶四元数的基本知识，基于对偶四元数描述的航天器近距离操作相对系统的运动学和动力学方程，执行器故障的数学模型以及考虑到的故障模式，本文的控制目标也在本节给出。

1.1 对偶四元数

对偶数由Clifford[15]提出，后由Study[16]进一步完善。算子ε表示一个对偶单元并且满足ε2=0,ε≠0。对偶四元数是传统四元数和对偶数的结合，可以表示为：

(1)

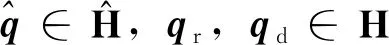
(2)

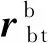
1.2 相对运动的运动学和动力学

基于对偶四元数描述下的6自由度航天器近距离操作相对运动学和动力学模型分别表示为：

(3)

(4)

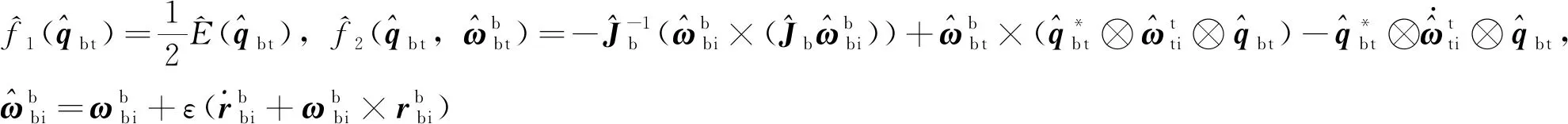
(5)

(6)

(7)

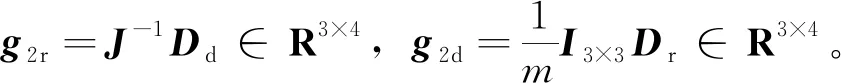
1.3 故障模型

故障信号可以参数化为

(8)

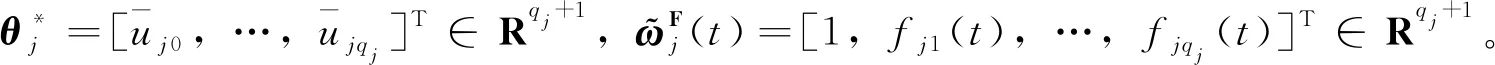
(9)

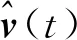
(10)

其中：σr=diag{σr1(t),σr2(t),σr3(t),σr4(t)}，σd=diag{σd1(t),σd2(t),σd3(t),σd4(t)}为对偶对角执行器故障模式矩阵，当σi(t)=1时表示第i个执行器故障，否则σi(t)=0，i=r1,…,r4,d1,…,d4

(11)

注意为保证航天器发生故障后的可控性，执行器故障需满足以下执行器冗余条件：rank(Drσr)=3和rank(Ddσd)=3。

本文主要考虑如下三种可能的故障：

(1)无故障：ui(t)=vi(t),i=r1,…,r4,d1,…,d4；

(2)ur1故障：

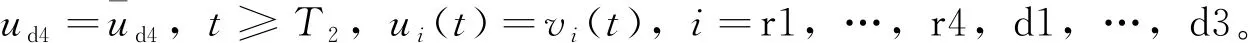
选择ur1和ud4故障补偿研究和选择其他的故障模式具有相同的技术难度，但便于控制策略的展示。而故障同时在推力器和反作用轮上发生的故障模式等同于故障模式(2)和(3)的结合。

1.4 控制目标

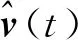
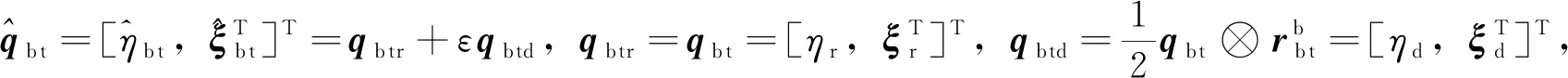
(12)

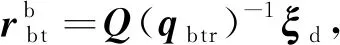
2 自适应执行器故障补偿

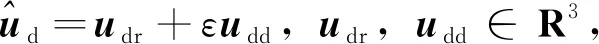
(13)

仍需要被满足。

2.1 标称故障补偿设计

首先在假设故障模式，故障值都已知的情况下为三种故障情况分别设计三个标称故障补偿控制器结构。

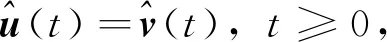
(14)

(15)

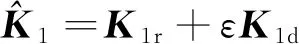
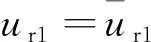
(16)

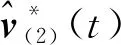
(17)

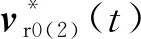
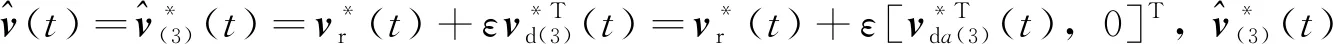
(18)

(19)

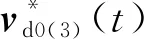
融合以上的3种单故障补偿控制器可得标称控制器如下：

(20)

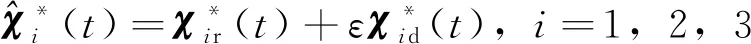
(21)

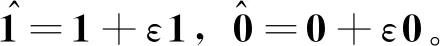
2.2 自适应执行器故障补偿

由于未知追踪航天器的执行器故障模式、故障值、故障发生时间，所以航天器近距离操作相对运动系统亟需一个自适应故障补偿方案。

2.2.1 自适应控制器结构

自适应控制器的结构可以表示为

(22)

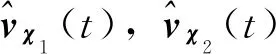
(23)

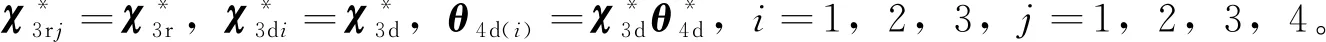
εdiag{χ1d1,χ1d2,χ1d3,χ1d4}h1dK1dudd

(24)

vχra(2)(t)=χ2rvra(2)(t)

=diag{χ2r1,χ2r2,χ2r3}h2rK2r1udr+

(25)

vχ2d(t)=χ2dh2dvd0(2)(t)

=diag{χ2d1,χ2d2,χ2d3,χ2d4}h2dK2dudd

(26)

vχ3r(t)=χ3rh3rv0(3r)(t)

=diag{χ3r1,χ3r2,χ3r3,χ3r4}h3rK3rudr

(27)

vχda(3)(t)=χ3dvda(3)(t)

=diag{χ3d1,χ3d2,χ3d3}h3dK3d1udd+

(28)

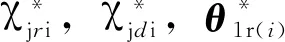
在本文中，自适应控制策略会被应用在带有未知故障模式、故障值以及故障发生时间的航天器近距离操作相对运动系统(3)和(4)中。

2.2.2 Backstepping控制设计

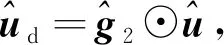
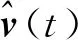
α=-k1Δ-1e1

(29)

其中：k1>0是一个给定的常数。

(30)

(31)

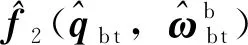
(32)

其中：

(33)

(34)

(35)

(36)

(37)

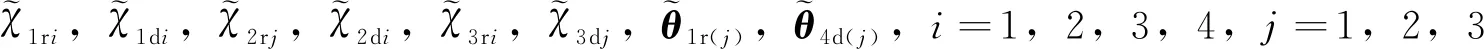
(38)

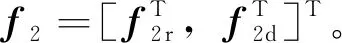
2.2.2 自适应律

本节将会给出控制器参数χjri，χjdi，θ1r(i)和θ4d(i)的自适应律。

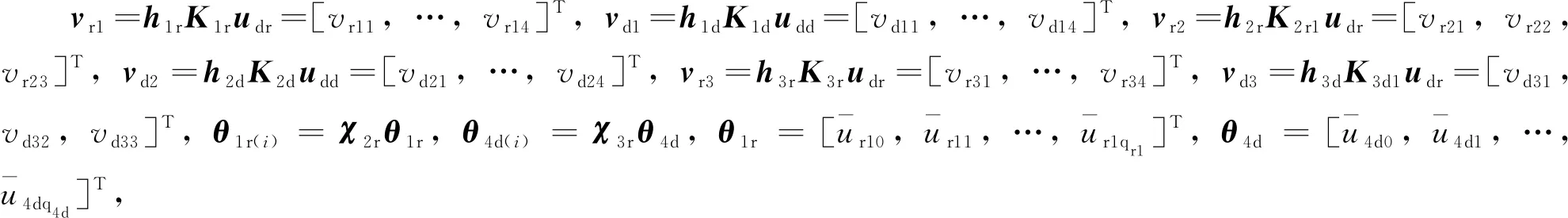
=[θ1r(i)(0),θ1r(i)(1),…,θ1r(i)(q1r)]T

(39)

=[θ4d(i)(0),θ4d(i)(1),…,θ4d(i)(qd4)]T

(40)

选择自适应律如下：

(41)

2.2.3 性能分析

系统全局稳定性分析如下。首先给出定理1。

证明：定义[Ti,Ti+1)，i=0,1,2为执行器故障模式固定的时间间隔，其中：T0=0，T3=∞。假定ur1在T1发生故障，并在[T1,T2)保持故障；假定ud4在T2发生故障，并在[T2,T3)保持故障。

针对无故障情形，考虑如下李雅普诺夫函数

(42)

那么，V1的时间导数为

(43)

同样地，可以得到针对ur1和ud4故障情形的李雅普诺夫函数V2和V3：

(44)

(45)

V2和V3的时间导数分别为

(46)

(47)

3 仿真验证

本节将给出将设计的自适应故障补偿方案应用于控制航天器近距离操作相对运动系统来验证其有效性。数据来源于文献[11]。

3.1 仿真条件

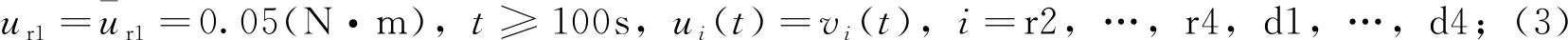
3.2 仿真结果

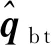
图1 系统误差 e1Fig.1 System error e1

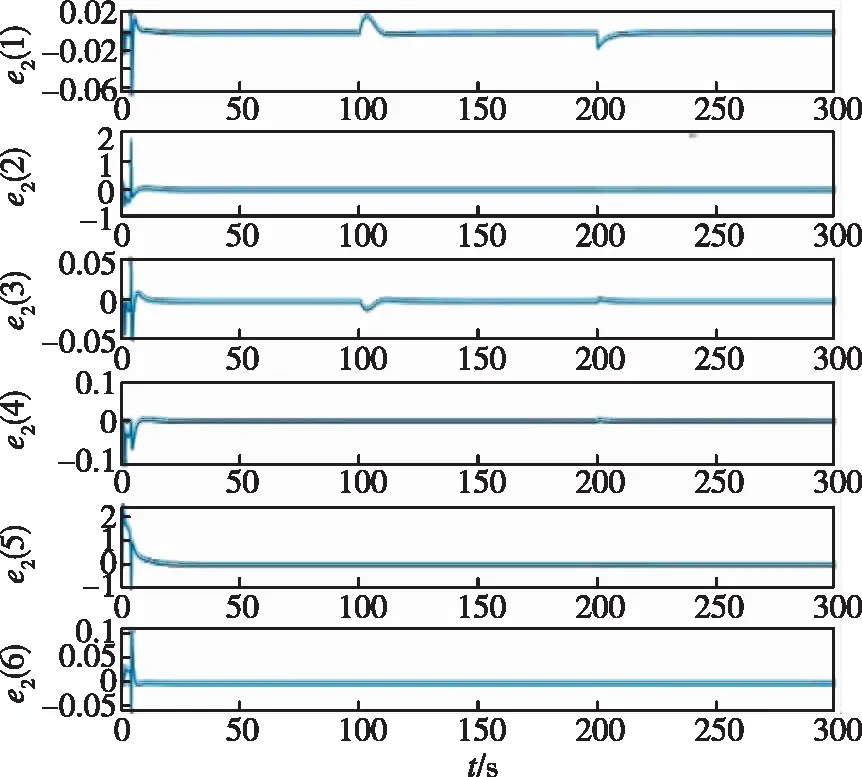
图2 系统误差e2Fig.2 System error e2

4 结 论

本文针对有执行器故障的基于对偶四元数描述的航天器近距离操作系统，设计了一个基于多设计融合的自适应容错控制方案。该方案能够使得追踪航天器在有执行器故障的情况下，位置和姿态信息都能跟踪上目标航天器。该方案的设计核心是通过用故障模式参数和故障值参数的自适应估计来构建故障补偿器，使得考虑到的所有故障都得以补偿。仿真结果也表明了该方案的有效性。同时，本文没有考虑到追踪星的转动惯量和质量的不确定性，可在本设计方案的基础上拓展研究。