时变论域下设施智能滴灌系统的模糊PID控制

王 正，孙兆军

(1.宁夏大学新华学院，银川 750021；2.宁夏大学土木与水利工程学院，银川 750021；3.宁夏大学环境工程研究院，银川 750021；4.教育部中阿旱区特色资源与环境治理国际合作联合实验室，银川 750021)

目前，应用智能灌溉系统[1-3]是提高农业用水利用效率最广泛的方式，通过人工智能算法、自动控制理论交互机制，使智能灌溉系统可以配置出符合作物生长规律和需水要求的控制策略[4,5]，同时完成灌水设备参数的优化和管理[6]，实现精确控制、精准供水。

然而，智能灌溉系统是时变非线性系统，具有大时滞、大惯性以及多随机干扰等特点[7]，这将对系统的可靠性和稳定性产生重要影响。研究表明，优化算法与模糊PID结合形成的交互控制策略可有效地解决这些问题。张志柏等[8]提出利用遗传算法来调整PID参数的方法，结果表明该方法可提高参数的搜索精度，缩短稳态响应时间；赵亮等[9]将Fuzzy-PID直接应用于温室节水控制系统中，可使系统的鲁棒性增强，节水率约提高23%；吴兴利等[10]设计了基于模糊控制的智能滴灌装置，结果表明该装置能准确地采集土壤水分数据，进行精准供水控制，且相比对照，作物长势更好；田思庆等[4]采用模糊控制方式对部分灌水器进行了有效控制，结果表明该方法可提高水资源利用效率，促进作物生长；刘洪静等[11]设计了基于Modbus协议的模糊PID算法对灌溉设备实施智能控制，结果表明灌溉系统振荡时间缩短，最大超调量减小；李建军等[7]和刘东等[12]将BP神经网络算法应用于模糊PID的参数调节，结果表明该方法可实现精量灌溉；吴迪等[13]提出将模糊PID与变频器结合控制地下恒压灌溉系统，结果表明能有效抑制超调，缩短响应时间，节能40%以上，节水35%以上。

虽然智能算法与模糊PID控制结合能较准确地配置和管理设施智能灌溉设备，但当土壤环境和灌水条件等外部干扰输入变化时，智能算法仅能优化模糊PID 控制器的参数，而不能自适应调整模糊规则，故易产生较大的误差。因此，本文于设施智能滴灌系统模糊PID控制中引入时变论域算法，建立时变论域下的模糊PID控制器模型，运用模糊数学推理实现PID参数和模糊规则的自适应调整，提高控制精度。

1 智能滴灌系统数学模型

本研究的设施智能滴灌系统结构如图1所示。主要由决策管理和数据显示模块(模糊PID控制器)、数据采集模块(湿度传感器、电磁阀)、可编程控制器控制柜(Programmable Logic Controller，PLC)和系统执行模块(水泵、水表)等组成。

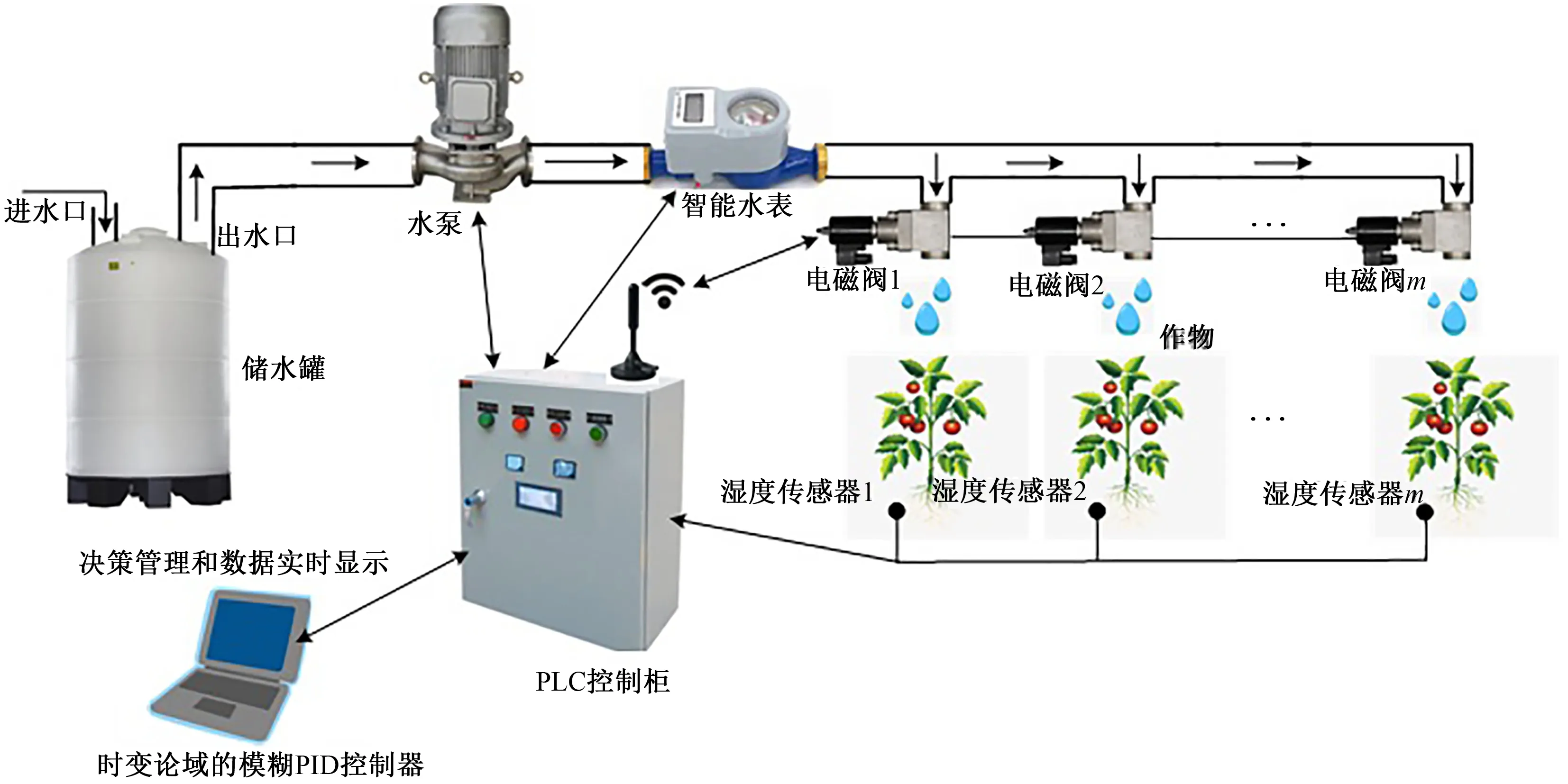
图1 智能滴灌系统示意图

通过建立水泵电机、水泵供水系统和其他控制及检测元件等环节的数学模型，进一步构建智能滴灌控制系统的传递函数。智能滴灌系统是利用变频器来调节水泵供水量，而变频器调节水泵电机转速过程可近似为一个惯性环节[14]，惯性环节时间常数为T1，其大小由变频器和水泵性能决定，数学表示为：

(1)

式中：K1为放大系数；T1为惯性环节时间常数；Nm(s)为水泵电机转速nm(t)的Laplace变换；F(s)为变频器输入频率f(t)的Laplace变换。

智能滴灌系统采用变压供水模式，即供水压力不断增加，增加到某一值时维持稳定，由压力上升阶段和恒压阶段组成。变压供水过程可用时间常数为T2的惯性环节和时间常数为τ的延时环节串联近似描述[9]，其中，T2的大小由滴头数量决定，τ的大小由管网长度及水流速度决定，数学表示为：

(2)

式中：K2为放大系数；T2为惯性环节时间常数；Np(s)为水泵转速np(t)的Laplace变换；P0(s)为水泵输出供水压力p0(t)的Laplace变换。

通常，可理想化地将系统其他控制及检测元件的数学模型假定为比例环节，数学表示为：

G3(s)=K3

(3)

为简单起见，认为系统中电机转速nm(t)与水泵转速np(t)相等，即nm(t)=np(t)，故整个供水系统闭环传递函数可表示为：

(4)

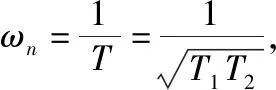
研究表明[15]，智能滴灌系统在工况较为稳定、变频器频率降低时，可用模型(2)近似描述，而当工况变化较大、较快或变频器频率增加时，系统需要用结构更为复杂的模型(4)近似表示。本研究为了更好地验证控制方法的有效性，选择模型(4)进行模拟仿真，试验测得的数据利用MATLAB R2014a编写程序进行反演，得到模型(4)的参数为：K=1.062 9，τ=0.370 3，T=0.536 1，ωn=1.865 3 rad/s，ζ=0.814 4，故传递函数为：

(5)

2 时变论域下模糊PID控制

时变论域下模糊PID控制的智能滴灌系统方框图如图2所示。根据智能滴灌系统控制流程构建有反馈回路的结构：经湿度传感器测得的土壤实际湿度反馈回决策管理设备，形成负反馈，同时，将湿度误差e和误差变化率ec的值实时送入控制器并参与控制作用，通过变论域算法进行PID参数、模糊规则的整定和校正，实现土壤湿度的智能控制，确保土壤湿度始终维持在给定值附近，与传统模糊PID相比，时变论域的模糊PID控制过渡过程时间更短、抗干扰能力更强。

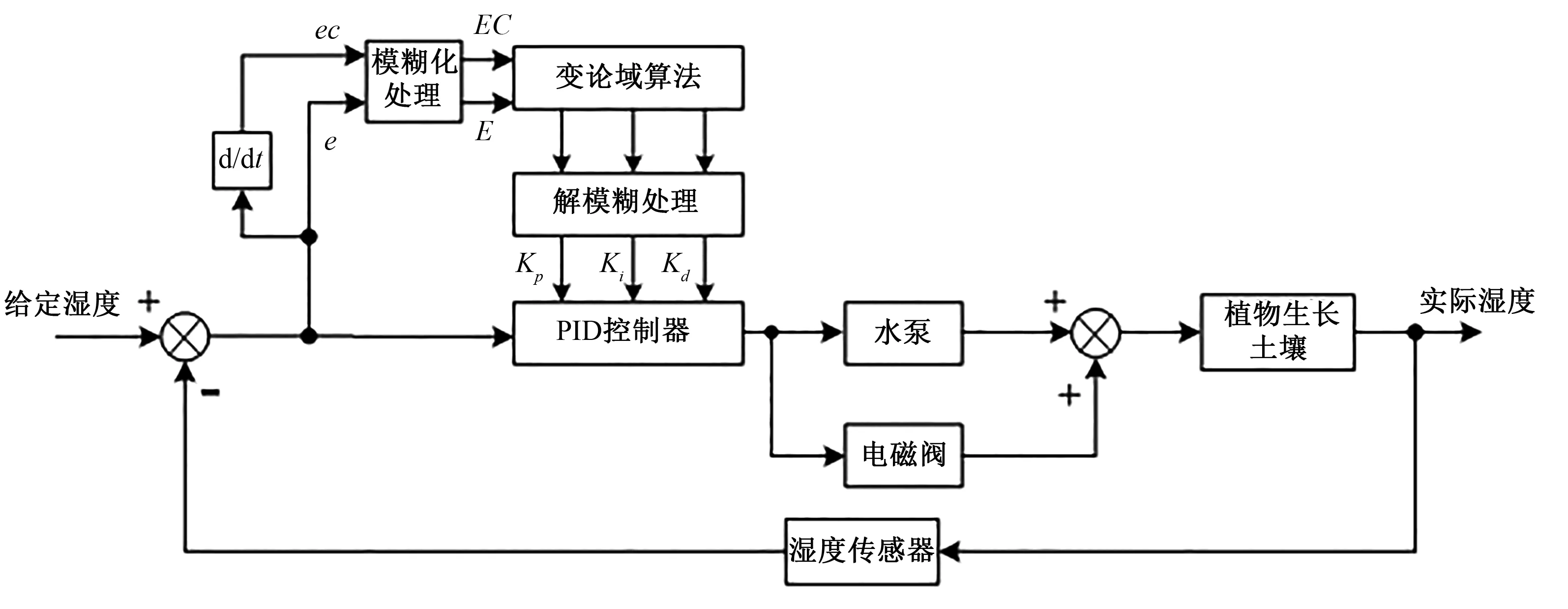
图2 基于时变论域的模糊PID系统方框图

2.1 模糊PID控制策略

通过向专家咨询及以往参数识别的经验，制定以下控制规则：

(1)当土壤湿度迅速上升接近于给定值时，湿度误差e为正值且逐渐减小，湿度误差变化率ec为负值且其绝对值增大，此时应增大Kp，而Ki、Kd尽量较小，而后为保证不出现较大超调量，应减小Kp和Ki，且增大Kd。

(2)当系统输出超过给定值并持续增加时，湿度误差e为负值且逐渐增大，湿度误差变化率ec仍为负值但变化速率减缓，此时应通过减小Kp来抑制过大超调量，同时增大Ki和Kd来加快过渡过程，使系统响应变快。

(3)当系统输出再次接近给定值时，湿度误差e为负值且逐渐减小，湿度误差变化ec为正值且逐渐增大，此时应尽量消除误差、加快响应，选择增大Kp，而后为避免出现振荡，选择减小Kp和Kd，增大Ki。

(4)随着时间推移，系统误差逐渐消除，此时选择增大Kp和Kd。

通过以上分析，可以得到智能滴灌系统模糊PID控制中Kp、Ki和Kd3个参数的控制规则，如表1所示，根据表1，可以写出系统在不同情形下的模糊规则，实现PID参数的自适应调整。

表1 模糊PID控制规则

2.2 时变论域伸缩因子

由于系统易受环境变化影响，为提高模糊规则的适应性和参数的准确性，需要引入时变论域来提高控制器对输出值的辨别能力。时变论域模糊控制，即引入随时间变化的模糊论域以适应系统输入变化和环境改变，通过添加输入和输出伸缩因子使模糊论域跟随湿度误差e及误差变化率ec的数值变动而实时调整[16]。其策略为：当土壤实际湿度与给定湿度之间差距较大时，采用较粗的模糊划分；当土壤湿度逐渐被控制系统调节接近给定值时，采用较细的模糊划分，并收缩论域范围。本文选取固定函数变化的伸缩因子[17]，其中，输入论域为α1(x)、α2(x)，输出论域β1(x)、β2(x)、β3(x)。具体表达式为：

输入伸缩因子：

α1(x)=1-λ1e-k1x2，α2(x)=1-λ2e-k2x2

(6)

输出伸缩因子：

3 仿真测试与结果分析

为验证时变论域下模糊PID控制系统的有效性，在MATLAB R2014a/simulink平台进行建模与仿真，其结构如图3所示。

通过不断调试，设定模糊PID控制器的3个参数初始值分别为Kp0=0.95，Ki0=0.50，Kd0=0.40时，控制效果较好。考虑最佳土壤湿度为50%左右，因此，在本研究仿真测试中假定土壤湿度初值为0，用大小为0.55的阶跃输入信号对智能滴灌系统分别进行PID、模糊PID和时变论域模糊PID等3种控制方法的仿真实验，仿真时间设置为20 s，采样周期为0.1 s，结果如图4所示。

根据图4可知，与PID、模糊PID相比，时变论域下模糊PID控制的智能滴灌系统的土壤湿度响应曲线较平滑，过渡时间短，无超调量，稳定性较强，调整时间短，稳态误差较小，但上升时间略长，表明系统能很快地进入稳定工作状态，具有更好的稳定性和鲁棒性，它们的各项性能指标对比如表2所示。

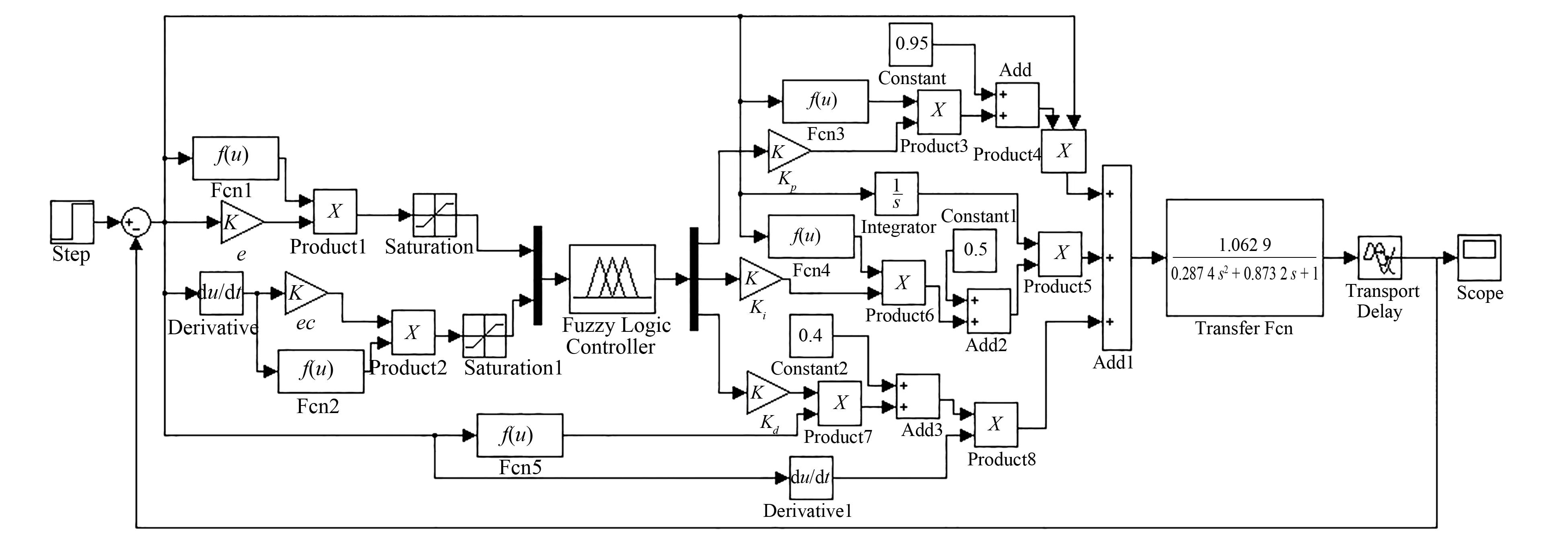
图3 智能滴灌系统的Simulink模型

图4 土壤湿度仿真曲线

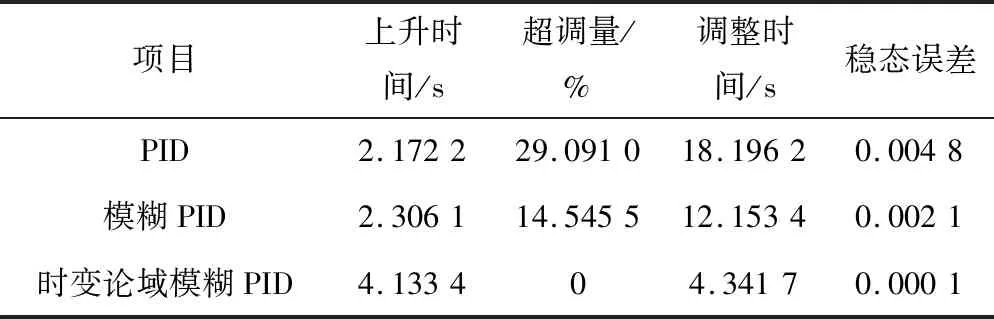
表2 控制系统各项性能指标对比

4 系统测试

于2019年2月在宁夏灵武市某蔬菜大棚中，针对智能滴灌系统的功能、性能、安全性等进行测试，测试周期为80 d，系统7×24 h不停歇运行。对比分析了系统控制的土壤湿度和灌水量，实验结果如表3所示。从测试结果可以看出，当设定土壤湿度为35%～69%时，相对误差不超过0.7%，当灌水量为39%～93%时，相对误差不超过0.5%，表明系统能精确控制灌水量和土壤湿度，满足灌溉要求。

5 结 语

本文论述了时变论域下智能滴灌系统的模糊PID控制方法，通过时变论域算法实时调整PID参数和模糊规则，并对实时数据进行管理和显示，实现了设施智能滴灌系统的智能化和精细化。通过系统仿真与测试，显示该系统工作状态良好，响应速度较快，稳定性和适应性较好，具有较好的应用价值。

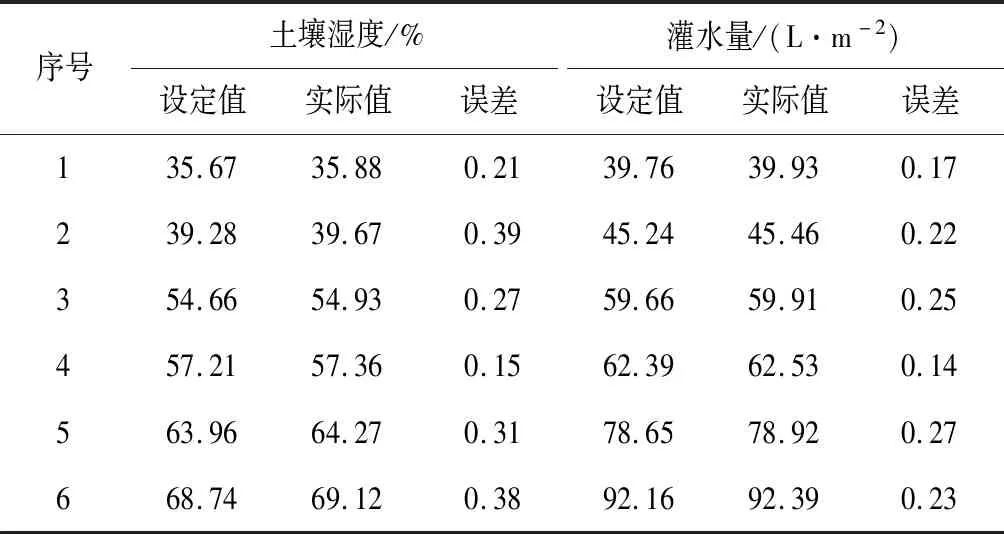
表3 智能灌溉系统测试数据

注：误差表示实际值与设定值之间的差值。