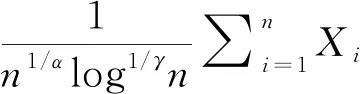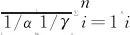END随机变量加权和的最大值序列的完全收敛性
陶惠玲,李翔,沈爱婷
(安徽大学数学科学学院,安徽 合肥 230601)
0 引言
在概率论与数理统计中,END序列是一类非常宽泛的随机变量序列,它包括独立随机变量序列,NA序列,NOD(negatively orthant dependent)序列是其特例.而像最小二乘估计、递归密度核估计、非线性回归核估计等常常表现为随机变量加权和的形式,因此对END随机变量加权和的极限性质的研究是非常有必要的.
Sung[1]对同分布NA随机变量序列的加权和获得了如下完全收敛性结果.
定理0.1[1]设1<α≤2,γ>0,{X,Xn,n≥1}为同分布的NA随机变量序列,{ank,1≤k≤n,n≥1}为常数序列,且满足
(1)
假设EX=0,且
(2)
则对任意的ε>0,
(3)
Chen 和 Sung[2]在比E|X|α<∞ 弱的矩条件下,得到了下面的结果.
定理0.2[2]设1<α≤2,0<γ<α,{X,Xn,n≥1}为同分布NA随机变量序列,{ank,1≤k≤n,n≥1}为常数序列,且满足(1) 式.假设EX=0,且
E|X|α/logα/γ-1(1+|X|)<∞
(4)
则对任意的ε>0,(3) 式成立.
Chen和Sung[3]在NOD序列下,证明(3) 式也成立.在同样的条件下,Huang[4]证明了(3)式对ANA(asymptotically negatively associated) 序列也成立.本研究的目的就是在END随机变量序列的情形下证明 (3) 式也成立,而且不需要同分布的假定,只需要随机控制就可以了.
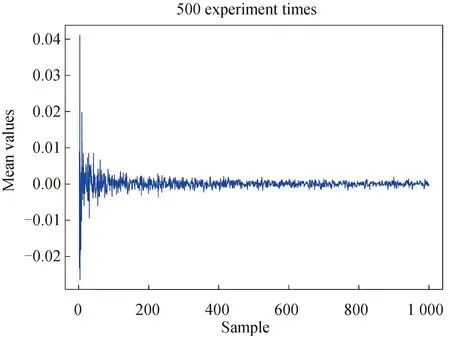
注0.1对任意的0 对任意的q>α,由(1)式可得 这两条性质在本文中主要定理的证明过程中会多次用到. 接下来介绍END随机变量序列的概念,最早是由Liu[5]提出的,具体如下: 定义0.1称随机变量序列{Xn,n≥1}是END随机变量序列,若存在常数M≥1,使得对任意的x1,x2,…,xn∈R,n≥1,都有以下二式成立: 由END随机变量的定义知,当M=1时,END序列即为NOD序列,可参考文献 [6].而NOD变量包含NA变量作为特例.因此,END随机变量包含独立变量、NA变量、NOD变量作为其特例,对其概率极限性质的研究具有很重要的理论意义和实际价值. 自从Liu[5]于2009年给出END随机变量的概念后,很多概率统计学者对此产生了浓厚的兴趣,并取得了很多有意义的结果.Chen等[7]建立了END随机变量的强大数定律,并给出在风险理论和更新理论中的应用,Shen[8]建立了END 随机变量的一些概率不等式和矩不等式,特别是Bernstein不等式和Rosenthal型矩不等式,同时给出在非参数回归模型中的应用,Wu等[9]给出了END随机变量部分和的一些收敛性质,Wang等[10]在一致变化尾下,建立了END随机变量的一个广义的大偏差结果,Qiu 等[11]研究了END 随机变量的完全收敛性,Wu 等[12]给出了END随机变量阵列的完全收敛性和完全矩收敛性,Wang等[13]研究了END误差下非参数回归模型中加权估计量的完全相合性,Yang等[14]得到了EDN误差下非参数回归模型中加权估计量的完全相合性的收敛速度,等.本研究在已有结果的基础上,进一步研究EDN随机变量的概率极限性质,特别是完全收敛性,所得结果推广了已有文献的相应结果. 完全收敛性是概率极限理论的一个重要内容,其概念最早由 Hsu和 Robbins[15]引入. 定义 0.2设{Xn,n≥1}是一随机变量序列,若存在常数C,使得对任意的ε>0,有 则称{Xn,n≥1}完全收敛于C. 显然,由 Borel-Cantelli 引理知,若{Xn,n≥1} 完全收敛于C,则Xn→Ca.s..因此,完全收敛性是一种比几乎处处收敛性更强的收敛性质,它可以用来建立随机序列加权和以及部分和的强收敛性,特别是强收敛速度. 本文中约定,C总代表正常数,在不同的地方可以代表不同的值;对于事件A,I(A)代表事件A的示性函数,#A表示集合A中包含的元素的个数.记logx=lnmax{e,x},x>0. 在这一部分,我们将给出一些必要的引理,他们在证明主要结果的过程中起到重要的作用. 第一个引理是END随机变量的基本性质,具体可参考文献 [16]. 引理1.1[16]设{Xn,n≥1}是END随机变量序列,{fn(·),n≥1}是同为单调递增(或同为单调递减)的函数列,则{fn(Xn),n≥1}仍是END随机变量序列. 下面的引理是END随机变量的Rosenthal型矩不等式,具体可参考文献 [8]. 引理1.2[8]设q≥2,{Xn,n≥1}是END随机变量序列,并且满足EXn=0和E|Xn|q<∞,n≥1.则存在只依赖于q的正常数C,使得下面不等式成立: 下面给出END随机变量序列的最大值的Rosenthal型矩不等式,具体可参考文献 [17]. 引理1.3[17]设q≥2,{Xn,n≥1}是END随机变量序列,并且满足EXn=0和E|Xn|q<∞,n≥1.则存在只依赖于q的正常数C,使得下面不等式成立: 本研究的主要结果需要用到随机控制的定义,具体如下: 定义1.1设{Xn,n≥1}为一随机变量序列.若存在随机变量X和一常数C>0,使得对任意的x≥0和n≥1,有 P(|Xn|>x)≤CP(|X|>x). 利用随机控制的定义以及分部积分,可以得到如下性质,他们在证明主要结果的过程中起到很重要的作用.具体可参考文献 [18] 或 [19]. 引理1.4[18-19]设{Xn,n≥1}为一随机变量序列,且被随机变量X随机控制.则对任意的α>0和b>0,有 E|Xn|αI(|Xn|≤b)≤C1[E|X|αI(|X|≤b)+bαP(|X|>b)], E|Xn|αI(|Xn|>b)≤C2E|X|αI(|X|>b), 其中C1和C2是两个正常数.从而有E|Xn|α≤CE|X|α,其中C是一个正常数. 定理2.1设1<α≤2,α<γ,{Xn,n≥1}是均值为零的END随机变量序列,且被随机变量X随机控制,满足E|X|γ<∞.设{ani,1≤i≤n,n≥1}是常数阵列,并满足 (1) 式.则对任意的ε>0,(3) 式成立. bn(logn)-βI(aniXi<-bn(logn)-β), I1+I2+I3. 因此,要证明 (3) 式成立,只需证明I1<∞,I2<∞以及I3<∞. 为了证明I1<∞,我们首先证明 (5) CE|X|α(logn)β(α-1)-α/γ→ 0,n→∞, 即(5)式成立.因此要证明I1<∞,只要证明 (6) 取 (7) 对固定的n≥1,令 An={1≤i≤n:|ani|≤n1/α(logn)-t}, Bn={1≤i≤n:|ani|>n1/α(logn)-t}. 易见 从而有 #Bn≤(logn)tα (8) 当α<γ<2 时,由引理1.3、Cr不等式和(8)式可得 J1+J2. 下面证明J1<∞,J2<∞.利用(7)式中t的取值范围以及(8)式可得 从而J≤J1+J2<∞,即(6)式成立. 当γ≥2 时,取一实数q,使q>γ.进一步取 由引理 1.3、Markov不等式、Cr不等式和(8)式可得 J3+J4+J5+J6. 下面分别证明J3<∞,J4<∞,J5<∞以及J6<∞,其中J3<∞与J5<∞的证明方法相同,J4<∞与J6<∞的证明方法相同.利用t的取值范围可得 由此可知J<∞,从而I1<∞ 成立. 为了使I2<∞,可以选N充分大,使得(1-βγ)N>1.类似地,我们可以证明I3<∞.定理证毕. 在定理2.1中,若ani≡ai,1≤i≤n,n≥1,则可得到如下推论. 推论2.1设1<α≤2,α<γ,{Xn,n≥1}是均值为零的END随机变量序列,且被随机变量X随机控制,满足E|X|γ<∞.设{an,n≥1}是常数序列,并满足 (9) 则对任意的ε>0, (10) 且 (11) 推论2.1的证明由(3)式,可立即得到(10)式.再由(10)式,可立即得到(11)式.证毕. 注2.1在推论2.1中,若取ai≡1,则由(11)式可得 (12) 在这一部分,我们将对(12)式的结果进行数值模拟,可取α=1.1,γ=1.2,用到的软件是R 软件.数据产生如下:对任意的n≥2,设(X1,Xn,…,Xn)′~Nn(0,Σ),其中0代表n维列向量,且 图1 固定样本下的变化情况 图2 不同样本下的变化情况1 引理
2 主要结果及其证明

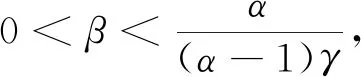

3 模拟