基于JMP软件的Lasso及岭回归在水稻全基因组预测中的应用

李亚男，陈建国

(湖北大学生命科学学院，湖北 武汉 430062)

0 引言

全基因组选择(genomic selection，GS)是利用分布在整个基因组上的分子标记来估算育种值的一种高效、经济的方法.它实质上是估计所有基因或染色体片段的联合效应，并结合这些效应来预测基因组估计的育种值(genomic estimated breeding value，GEBV)[1].由于GEBV的计算可以不依赖系谱记录和表型信息，这就为早期选择提供了可能，可以大幅度缩短育种年限，提高遗传进展，降低育种成本[2-3].

许多统计方法都可用于全基因组选择，包括贝叶斯方法(贝叶斯B)，最佳线性无偏预测(BLUP)，以及正则化线性模型(岭回归、Lasso回归和弹性网络)等[4].但是对于预测农作物的性状而言没有一种方法是完美的，它们各有各的特点，而预测的效果取决于模型的性质与性状的特点和遗传结构.影响全基因组选择(GS)模型预测精度的因素很多，这些因素是以复杂的方式相互关联的，包括模型性能、样本大小和亲缘关系、标记密度、基因效应、遗传力和遗传结构，以及连锁不平衡(LD)在标记与数量性状基因座(QTL)之间的分布等[5].

GS在动物育种中已经得到了广泛应用，但在作物育种中的应用起步较晚.目前提出的大多数全基因组预测方法都需要使用者具备编程能力，例如R语言，Matlab等，这对于实际育种工作者来说是非常大的挑战.统计软件JMP的算法源于SAS，特别强调以统计方法的实际应用为导向，交互性、可视化能力强，使用方便，尤其适合非统计专业的数据分析人员使用[6].在JMP中有专业的预测工具，广泛应用于业务分析领域，但在植物全基因组选择的预测方面的应用还很少.本研究利用JMP中的两种正则化线性回归方法(Lasso和岭回归)对水稻产量和产量相关性状进行全基因组预测分析，为育种工作者在选择合适的全基因组预测分析工具方面提供参考.

1 材料与方法

1.1 实验数据水稻的产量等性状的原始数据来自Yu等[7].实验人员将珍汕97 A和明恢63两个水稻品种作为亲本，杂交产生210个重组自交系(recombinant inbred lines，RIL)，从这些重组自交系中收集4个产量相关性状的表型数据，它们分别是水稻产量(YD)，千粒重(KGW)，分蘖数(TP)和单株谷粒数(GN).将各个重复的性状的平均表型值作为响应变量.基因组数据由水稻基因组的约270 000个SNP推断的1 619个组(bin)表示.组内的所有SNP都具有完全相同的分离模式(完全的连锁不平衡(LD))，因此来自一组的一个SNP足以代表整个组.210个RIL的基因型编码为：1代表珍汕97 A基因型，0代表明恢63基因型[8].

1.2 统计模型

1.2.1 Lasso回归 在全基因组选择中，预测变量的数目(p)通常远远大于个体的数目(n).在这种情况下，普通最小二乘法(ordinary least-squares，OLS)的估计值具有很差的预测能力，因为标记效应被视为固定效应，这导致预测变量之间的多重共线性和过度拟合，从而使该模型不可行[5].

Lasso(least absolute shrinkage and selection operator)是统计学家Robert Tibshirani在1996年提出的一种变量选择方法，它是OLS的约束版本，是一种基于线性回归模型的降维方法，对高维小样本数据的稀疏模型十分有用，在基因表达谱分析中被广泛应用[5].Lasso回归模型将任意选择一个并分解，而忽略其他Lasso模型[9]，这使得Lasso的惩罚期望许多系数接近零.该方法也广泛应用于具有大量数据集的领域，例如基因组学[5].

Lasso解是满足条件的α集，即：

其中λ≥0.Park和Casella[1]提出了贝叶斯版本的Lasso(贝叶斯Lasso)，并建议使用吉布斯采样器，其中αj服从双指数先验分布：

在Lasso回归中，Lasso的估计量使用l1惩罚最小二乘准则来获得以下优化问题的稀疏解，即：

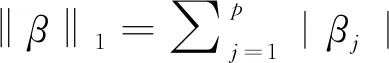
对于一些适当选择的λ，l1罚分使得Lasso能够同时调整最小二乘拟合并将β(Lasso)的一些分量收缩为零.循环坐标下降算法[10]有效地计算Lasso估计器的λ的整个Lasso解路径，并且比众所周知的LARS算法快.这些属性使Lasso成为一种吸引人且极受欢迎的变量选择方法.即便如此，Lasso算法有个关键的缺点，那就是对于高维数据而言不够稳定，即在p>n时，在饱和之前无法选择比样本大小更多的变量[8].尽管如此，Lasso方法在动植物的全基因组选择中仍是十分有效并广泛应用的一种方法[11]，并且Lasso及其扩展(包括弹性网和自适应Lasso)已用于各种QTL作图或基因组选择研究[12].

1.2.2 岭回归 如果有许多预测变量，则岭回归[8]是理想的选择，岭回归的非零系数从正态分布中提取[13].特别是，它对许多预测性状都表现出良好的性能.岭回归将相关预测变量的系数均等地收缩为零.例如，给定k个相同的预测变量，如果单独拟合，每个预测变量将得到大小等于1/k的相同系数[8].因此，岭回归不会强制系数消失，而且它不能选择仅具有最相关预测的预测子集的模型.

岭回归估计器在y=μln+Xβ+e中使用l2惩罚最小二乘解决回归问题：

岭回归方法可以同时估计GS的所有标记效应[2].岭回归不是将标记归为显著性或无效性，而是将所有标记效应缩小到零[7]，该方法假设标记是具有共同方差的随机效应[14]，其方差并不是假定所有标记都具有相同的效应，但这种标记效应都同样缩小为零.然而，假设各个标记具有相同的方差是不现实的，因此，这也是岭回归的一个缺陷.尽管不能正确地假定标记方差相等，但岭回归优于一般的全基因组选择方法，因为它可以同时估计所有标记的影响：通过避免标记选择，它避免了与选择相关的偏差，此外，岭回归方法比一般方法更适合于很少或没有大效应和许多小效应的情况下的预测，与大多数数量性状的情况一样[15].

1.3 数据分析用统计软件JMP14试用版(Trial)进行数据分析.数据文件包含4个因变量yield(产量)、kgw(千粒重)、tiller(分蘖数)及grain(单株谷粒数)，1 619个预测变量(SNP标记).Lasso回归和岭回归均在“分析”菜单下“拟合模型 >广义回归”对话窗口中进行设置和运行.利用“模型比较”命令对两种预测方法的效果进行评价.用于比较预测效果的指标是决定系数(R2)、均方根误差RASE(root average squared error)、平均绝对误差AAE(average absolute error)[16]和预测值与实际值的相关系数(r)[17].

2 结果与分析

表1列出了用岭回归和Lasso回归对产量、千粒重、分蘖数及单株谷粒数等4个性状进行全基因组预测的模型性能和预测效果评价指标的估计值，并在图1中对两种预测方法和不同性状的预测效果进行了比较.决定系数(R2)反映的是模型的拟合优度，均方根误差RASE和平均绝对误差AAE也是模型性能评价的常用指标，其中AAE受离群值影响较小；预测值与实际值的相关系数(r)在全基因组选择中通常被用来衡量预测的准确性.表1和图1的结果表明，两种预测方法对于4个性状都有较好的预测效果(最小的r=0.721 8)，但Lasso回归的模型拟合及预测效果一致地优于岭回归，其中拟合最好的是千粒重的Lasso回归预测模型(R2=0.932 5)，即模型解释了该性状变异的93.25%.图2是各性状的实际值-预测值图，从中可以看出岭回归预测值的变异性都大于Lasso回归.对于这两种预测方法，4个性状的模型拟合及预测效果的次序为：千粒重 >分蘖数 >单株谷粒数>产量.

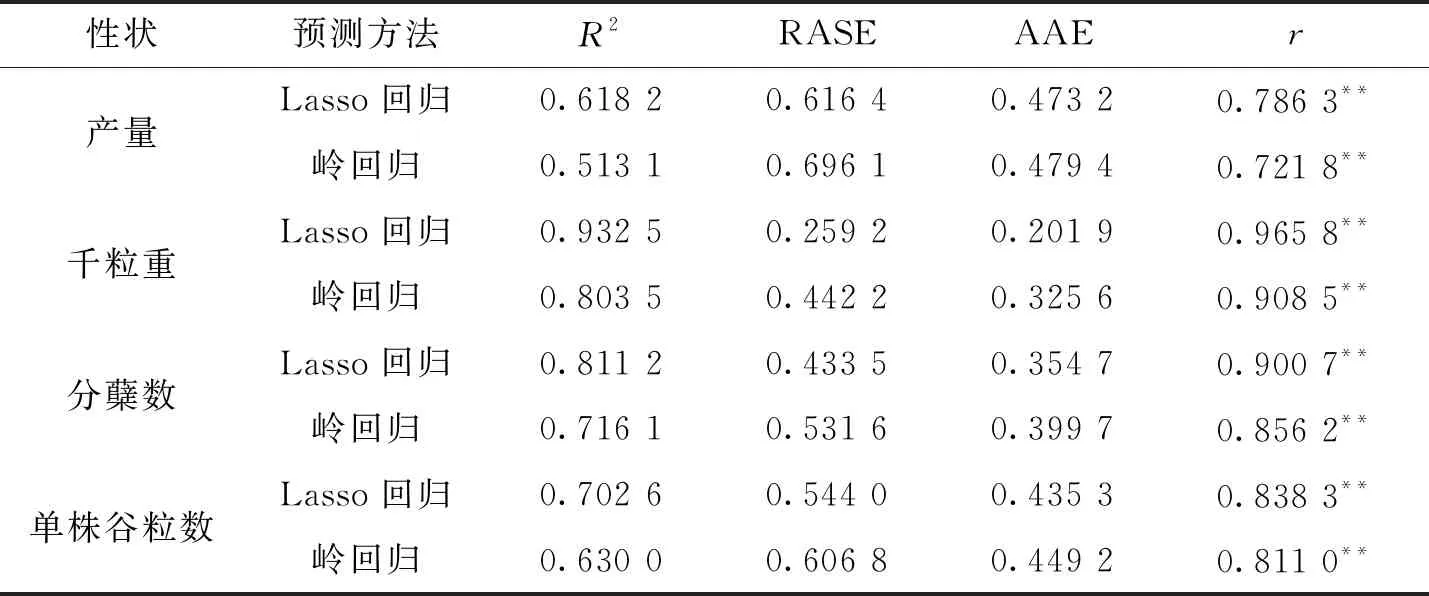
表1 用Lasso回归和岭回归对水稻4个性状进行全基因组预测的效果

**表示相关系数在α=0.01的水平上具有统计学意义

图1 各性状的Lasso回归和岭回归预测效果的比较

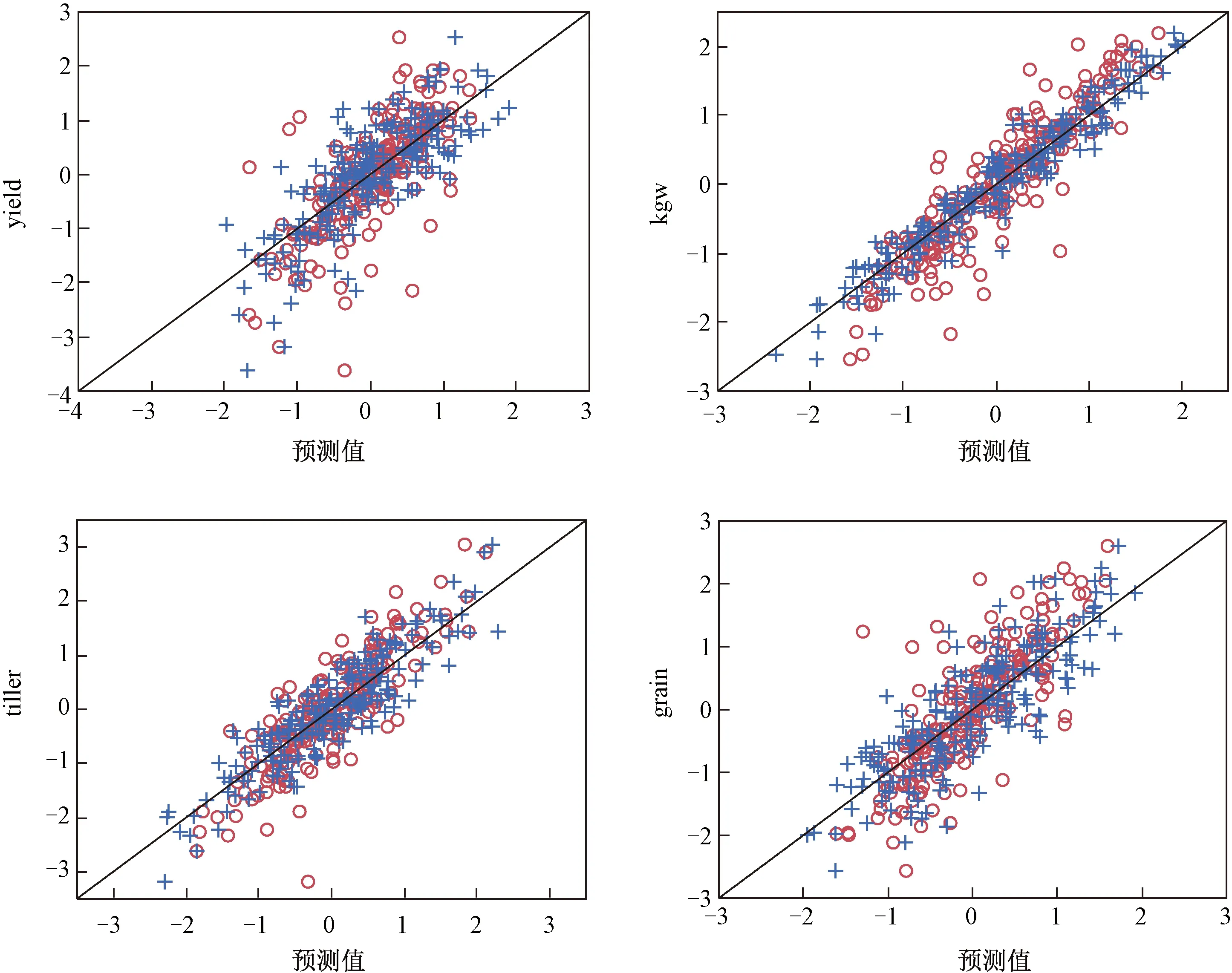
红色ο代表岭回归，蓝色+代表Lasso回归图2 各性状的实际值-预测值图

3 讨论

自20世纪90年代以来分子标记辅助选择(MAS)在植物育种中得到广泛应用，但MAS的应用取决于对主效基因的遗传作图和关联分析，选择周期较长，也无法利用微效基因的效应[18].全基因组选择(GS)使用高密度的分子标记，通过全基因组预测模型来克服这些局限性.全基因组选择不需要检测显著的QTL-标记位点关联，并同时考虑了大量的预测变量.此外，GS可以加快育种进程，提高单位时间和单位成本的遗传增益[19].

图3 产量的Lasso回归(a)和岭回归(b)的解路径图图中的每一条线代表了一个预测变量的模型参数

GS在动物育种中应用较早，但在作物育种中尚处于探索阶段[20].在GS中，全基因组标记的基因型数据与性状表型数据一起分析，以估计与每个标记关联的性状的表型效应.已经提出了大量的标记效应估计模型，比如逐步回归、岭回归、贝叶斯估计模型、半参数回归和机器学习方法[21].但这些方法的实施大多要求使用者具备一定的编程能力.本研究利用统计软件JMP对水稻组合珍汕97 A×明恢63衍生的一个RIL群体的4个与产量相关的性状进行了全基因组预测.因为要从很少数目的表型观察值估计大量的标记效应，而且标记之间可能有高度的共线性，所以采用了两种正则化回归方法——Lasso回归和岭回归，这两种方法都属于惩罚模型，通过牺牲一些无偏性，可以大幅度减小方差，从而使整体的平均误差低于无偏模型[22].4个性状的结果表明，这两种预测方法都有较好的预测效果，但Lasso回归在所有性状中都优于岭回归，而且Lasso回归的运算速度远远快于岭回归.另外，岭回归虽然可以将参数估计值向0进行收缩，但它不能将系数取值变为严格的0，因此并没有进行变量选择的能力.而Lasso回归使用了与岭回归类似的惩罚项，并且在对模型进行控制的同时，还能够进行变量选择[22].比如在产量的Lasso回归分析中，经过两轮迭代后，模型中只剩下34个对模型有贡献的预测变量(标记)，而在岭回归中，所有预测变量都没有从模型中剔除(图3).其余性状也有类似的情况.基于以上的结果，我们认为可以用JMP软件来对作物进行全基因组预测，对于所分析的4个水稻性状而言，选用Lasso回归比岭回归更好.