初中数学习题教学有效性的提高策略探讨

摘要：习题教学是初中数学课堂的重要环节，能够巩固学生对数学理论知识的掌握程度，锻炼学生的知识应用能力，有效培养学生的数学思维，通过良好的习题解答实践，学生也能够体味到数学学习的乐趣。本文从精准审题、联想应用、深刻反思三个方面入手，对初中数学习题教学策略展开探究，旨在有效提高习题教学成效，不断提升学生数学核心素养。

关键词：初中数学;习题教学;审题;联想;反思

数学习题高质高效地利用，对于初中数学教学有效性的进一步深化提升具有强力的支撑作用。传统教学模式下，习题教学的开展主要是对练习题进行讲解，但并未给学生提供一个反思的空间，导致习题教学质量并不理想，初中数学习题教学的有效策略需一线教师深研。在新课改大环境下，初中数学习题教学的开展，需要对教学模式进行优化，将数学解题思维与方法提炼出来，通过深度剖析来提高学生解题能力，这对于学生数学水平的提升也至关重要。

一、 引导学生精准审题

在数学学习过程中，审题是一种关键的能力，在初中数学习题教学过程中，引导学生精准审题，能够明确具体的解题思路，从而顺利解题。审题在数学习题解答中居于重要地位，这就需要学生在面对数学题目时，要具备审题意识，对题目内容进行仔细阅读和认真揣摩，对关键信息进行深度挖掘，把握解题关键点，逐步提高学生审题能力，保证数学题目解答的目的性与高效性。

（一）认真梳理题目类型

数学题目解答过程中，审题是一个基础环节，需要辨析题目类型，对解题方法加以正确运用。对于选择题、填空题、判断题等类型题目，可直接运用求解法、图解法等，通过答案或者反证法来对答案选择是否正确进行验证。对于解答题，一般需要围绕题设条件出发来进行分析，探寻解题思路，合理运用数形结合思想，求解过程中主要运用配方法、换元法、待定系数法等，解答题往往是综合化的考查知识点，因此在对证明方法进行选择时，可应用分析法、综合法、反证法等，保证题目解答的正确性，解题效率也逐步得到提升。

（二）认真分析题设条件

审题过程中必须要就题设条件进行梳理，以便开展综合分析，明确已知条件与求解目标，以便找寻解题思路。题目难度往往决定着题设条件的多与少，在初中数学习题教学过程中，需要遵循先易后难的原则来指导学生解题，将题目难度进行合理化解，在学生掌握简单题目的解答方法后，再去探究复杂的数学题目，以便更高效地进行解题。在难题解答过程中，需要对解题方法加以灵活运用，循序渐进的探寻解题路径，以确保题目解答的正确化。在审题过程中需要就已知条件进行分析，对隐含条件进行挖掘，逐步培养学生良好的审题习惯。教师需要引导学生认真读题，仔细审题，明确题目条件及内涵，准确获取信息，挖掘各项题设条件，对求解目标进行深入探究，以确保解题方法正确。

（三）深入把握审题关键

审题的目的性较强，在题目解答过程中，需要明确题目条件以及求解目标，明确解题的中间条件，审题效率也能够得到保证，从而有效节约解题时间，确保学生正确解题。

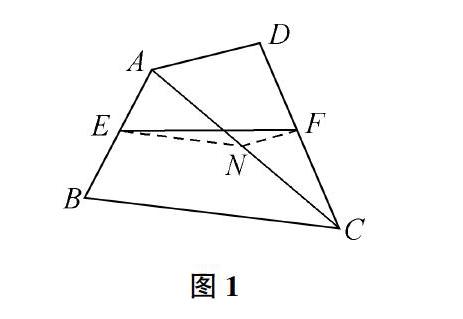
比如，“如图1，在四边形ABCD中，E和F为AB、DC的中点，对角线AC的中点为N，求证：BC+AD≥2EF。”

图1

通过审题可知，在这一证明题中，以四边形中两条对边长度之和大于或者等于另外两条对边中点连线的2倍为求证目标。据此应用分析法进行解题，基于题设条件出发，明确题目所涉及的知识点，联想到隐藏条件“中位线”。将EN、FN进行连接，两个三角形的中位线得以形成，这就为顺利求证提供了条件。从BC=2EN，AD=2FN可知BC+AD=2（EN+FN），而EN+FN≥EF，通过推导可知BC+AD≥2EF。因此在数学习题解答过程中，需要就题设条件进行分析，把握审题关键，挖掘隐含条件，探寻求证方法，从而促进数学题目的顺利解答。

二、 引导学生联想应用

在理解题意的基础上，可锻炼学生的联想应用能力，围绕题目中的知识点及解题要点进行思索和推测，为顺利解题提供支持。数学知识的邏辑关联性显著，因此数学题解答过程中，要重视联想作用的发挥。

（一）关注知识纵横关联

在审题的基础上，需探索科学且正确的解题方法，在这一方面，联想发挥着重要的作用，能够对学生数学视野加以拓宽，便于学生把握数学知识点的纵横关联，把握解题方法的灵活性与创造性，学生数学解题思维也得以夯实。在初中数学习题教学过程中，可从两个方面入手，其一是从结果分析原因，就所需条件进行联想;其二是从原因探索结果，立足题设条件及隐含条件来进行挖掘，获得结论，对相关定理、定律等知识点进行联想，以便进行推理论证，从而顺利解题。

（二）明确联想应用过程

就几何证明题来说，通过联想的应用，能够有效发散学生的思维，促使学生举一反三灵活地运用所学知识进行解题，从而有效强化学生数学思维能力。

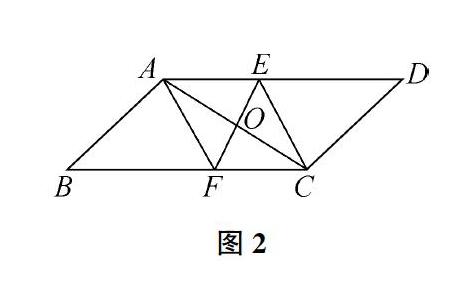
比如，“如图2，在平行四边形ABCD中，对角线为AC，AC的垂直平分线为EF，求证：四边形AFCE为菱形。”

图2

解答这一习题，可引导学生从结果出发“据果探因”，即从求证的结论出发开展联想，要证明四边形AFCE为菱形，则需要把握菱形的判定定理，明确已知条件：①四条边都相等;②一组邻边相等的平行四边形;③对角线互相垂直平分的四边形。基于题设条件出发做出联想，AE∥FC，AE=FC，△AOE≌△COF，△AOF≌△COE。

若从原因探索结果，基于题设条件来开展联想，以平行四边形、对角线、垂直平分线作为入手点，对条件进行联想，就性质进行思考，可知AB=DC且AB∥DC;AD=BC且AD∥BC;∠BAD=∠BCD，∠B=∠D。AC的垂直平分线为EF，据此可知EA=EC，FA=FC，OA=OC。在全面联想后可知题目存在多种证明方法。

通过联想的应用，能够明确解题关键点，探寻解题思路，更加灵活的运用数学知识去解答问题，促进学生数学水平的显著提升。

三、 引导学生深刻反思

对于个体来说，反思是一种优良的品质，能够促进学习效率的改善。在初中数学习题教学过程中，通过反思的合理化运用，能够逐步提高学生的认知水平，培养学生数学学科核心素养，学生主动回顾解题思路，以精准审题和联想应用为支持，探寻科学合理的解题方法，妥善梳理知识点，明确彼此之间关联，以把握数学解题规律，探寻最佳的解决路径，循序渐进的提高学生数学解题能力。

（一）以反思促进触类旁通

数学题目解答后并不表示学习任务的完成，需要在教师的指导下，以反思为主要途径，对解题方法加以深刻领会，在回顾与思考的空间中，学生能够结合自我知識水平进行反思，明确解题过程中所遇到的障碍，对条件挖掘是否到位等等，通过深刻反思，能够促进学生优良数学学习习惯的养成，逐步提高学生自主学习能力，这对于学生的全面发展具有重要意义。在初中数学习题教学过程中，通过深刻反思，学生能够明确数学知识点之间的密切联系，对知识进行串联，这就有助于实现触类旁通，在对题型及解答方法进行总结的过程中，学生的数学问题解答能力得到逐步提升，并且在实践中积累数学解题经验，锻炼思维能力，这就有助于促进学生数学核心素养逐步提升。

（二）以习题探究反思应用

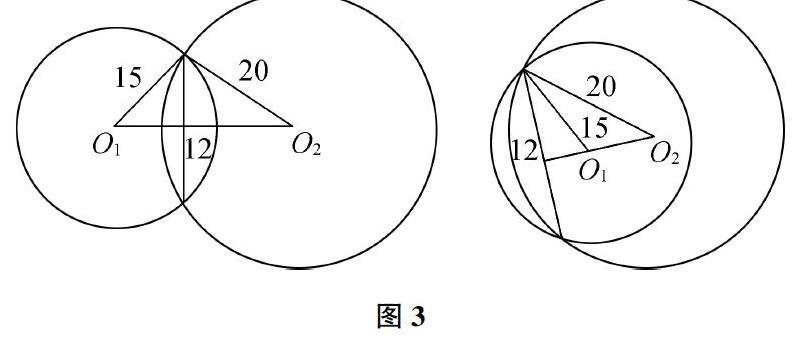
初中数学习题教学过程中，可围绕习题出发来引导学生进行反思，培养和锻炼学生的数学思维能力，有效提高学生数学解题能力。比如，“如果两个圆的公共弦长是24，两个圆的半径分别是15和20，求圆心距。”

基于题设进行精准审题，可知存在两种情况，如图3所示。①两圆相交，圆心距处于公共弦的两侧;②在公共弦的同侧。在解题过程中要进行差异化分析。通过计算可知，在第一种情况下，O1O2=25，第二种情况下O1O2=7。通过对解题方法进行反思，学生认识到分类思想在数学题目解答过程中的重要作用，在解题过程中分别对待可能与条件相符合的圆心距，这就能够促使学生以严谨的态度对待数学学科，在潜移默化中培养学生优良的数学学习习惯，促进学生数学思维的不断发展。

图3

总之，在初中数学习题教学过程中，必须要充分认识到审题、联想、反思的重要价值，引导学生在解题实践中加以科学应用，巩固学生数学基础，促使学生更好地运用所学知识去解决数学问题，强化学生探究思维能力，深化学生数学学习体验，在潜移默化中培养学生数学核心素养，为未来复杂数学知识学习打下良好的基础，初中数学习题教学目标也得以顺利实现。

参考文献：

[1]张月虹.论如何有效开展初中数学习题教学[J].中学教学参考，2020（2）.

[2]黄静亚.提升初中数学习题课教学效率的实践研究[J].中学数学，2020（1）.

[3]赵正萍.初中数学练习题的教学策略研究[J].数学教学通讯，2019（11）.

作者简介：

陈木清，福建省三明市，福建省三明市沙县第六中学。