大数据背景下的电子商务客户流失量预测

吴永春

摘  要： 针对当前方法无法对电子商务客户特点进行描述，存在电子商务客户流失量预测不准确，且电子商务客户预测效率低的缺陷，为了提高电子商务客户流失量预测结果，设计了一种大数据背景下的电子商务客户流失量预测模型。首先，分析电子商务客户流失量的研究进展，找到引起电子商务客户流失量预测结果不理想的原因;然后，采用模糊聚类分析算法对电子商务客户流失量数据进行预处理，减少电子商务客户流失量预测的训练样本规模，并采用最小二乘支持向量机建立电子商务客户流失量预测模型;最后，采用电子商务客户流失量实际数据对预测性能进行分析。实际数据测试结果表明，所提模型的电子商务客户流失量预测精度均高于95%，减少了电子商务客户流失量预测时间，为电子商务客户流失分析提供了一种有效的研究方法。

关键词： 客户流失量预测; 电子商务系统; 大数据; 模糊聚类分析; 预测模型; 数据预处理

中图分类号： TN911.1?34; TP391                    文献标识码： A                   文章编号： 1004?373X（2020）11?0144?04

Prediction of churn rate of e?commerce customers in context of big data

WU Yongchun

（School of Business， Shandong Jianzhu University， Jinan 250101， China）

Abstract： In veiew that the e?commerce customers have the characteristics of massive and big data， and the characteristics of e?commerce customers can not be described with the current methods， the prediction of e?commerce customer churn rate is inaccurate， and the prediction efficiency of e?commerce customers is very low. In order to improve the prediction effect of e?commerce customer churn rate， a prediction model of e?commerce customer churn rate in the context of big data is designed. The research progress of e?commerce customer churn is analyzed to find out the reason why the prediction results of e?commerce customer churn are unsatisfactory. The data of e?commerce customer churn is preprocessed with the fuzzy clustering analysis algorithm， so as to reduce the training sample scale of e?commerce customer churn prediction. The least squares support vector machine （SVM） is used to establish the prediction model of e?commerce customer churn. The actual data of e?commerce customer churn are adopted to analyze the prediction performance of the prediction model. The actual data test shows tha the accuracy of prediction model for the e?commerce customer churn is higher than 95%， which reduces the prediction time of e?commerce customer churn and provides an effective research method for analysis of the e?commerce customer churn.

Keywords： customer churn prediction; e?commerce system; big data; fuzzy clustering analysis; prediction model; data pre?processing

0  引  言

随着移动支付、互联网技术的不断成熟，由于网络购物透明性高、购买成本低，人们在网上购买的次数不断增加，这样电子网站成为了人们经常光顾的场所[1?2]。但是电子商务购物有一个最大的特点，就是客户极不稳定，有的客户只购一次，再也不会发生购买行为，再加上网络市场的竞争加剧，客户流失量相当高，因此如何留住客户，最大程度地降低电子商务客户流失率，是所有商家必须解决的一个问题[3?4]。电子商务客户流失的预测可以帮助商家发现客户流失趋势，有利于他们制定一个挽留措施，提高商家的利润，因此，电子商务客户流失量预测成为当前电子商务领域的一个重要研究方向[5]。

最原始的电子商务客户流失量预测通过经验阈值法进行，根据阈值对电子商务客户是否活跃来判断电子商务客户是否处于一种流失状态，该方法十分简单，但是有一个致命的缺陷，就是电子商务客户流失量预测误差大，预测结果的实际参考价值比较低[6?8]。随着大数据技术和人工智能技术的发展，人们将其引入到了电子商务客户流失量预测的研究中，如基于决策树的电子商务客户流失量预测模型、基于关联分析的电子商务客户流失量预测模型、基于神经网络的电子商务客户流失量预测模型、基于支持向量机的电子商务客户流失量预测模型等，相对于经验阈值法，这些大数据技术和人工智能技术的电子商务客户流失量预测结果更加准确[9?11]。随着电子商务客户流失量数据规模不断增加和影响因素的增多，电子商务客户流失量具有时变性、随机性、规模性等变化特点，这些模型的缺陷也慢慢体现出来，如决策树、关联分析只能对线性变化特点的电子商务客户流失量进行准确预测，使得电子商务客户流失量预测误差大，神经网络和支持向量机的收敛速度慢、学习时间长，使得电子商务客户流失量预测的效率低[12?13]。

结合电子商务客户具有海量、大数据特点，为了提高电子商务客户流失量预测的准确性，本文设计了一种大数据背景下的电子商务客户流失量预测模型。实际数据测试实例结果表明，本文模型的电子商务客户流失量预测精度均高于95%，减少了电子商务客户流失量预测时间，具有比较明显的优越性。

1  大数据背景下的电子商务客户流失量预测模型

1.1  模糊聚类分析算法

设有[n]个训练样本：[X={x1，x2，…，xn}]，每个样本有[m]个特征，即[xj=（x1j，x2j，…，xmj）]，那么训练样本集合的特征属性矩阵为：

[X=x11x12…x1nx21x22…x2n????xm1xm2…xmn] （1）

式中[xij]为第[i]个样本、第[j]个特征值。

对式（1）进行规范化操作，产生新的矩阵为：

[R=r11r12…r1nr21r22…r2n????rm1rm2…rmn] （2）

对所有样本根据特征属性进行分类迭代，共有[c]类，建立模糊聚类矩阵如下：

[U=u11u12…u1nu21u22…u2n????uc1uc2…ucn] （3）

每一个类有一个聚类中心，那么可以建立如下的模糊聚类中心矩阵[S]：

[S=s11s12…s1cs21s22…s2c????sm1sm2…smc] （4）

以欧氏距离的平方和最小為目标，目标函数可表示为：

[minF（uhj，sih）=j=1nh=1cuhjrij-sih2] （5）

1.2  最小二乘支持向量机算法

样本集合为[（xi，yi），i=1，2，…n]，最小二乘支持向量机采用映射函数[φ（?）]对其进行变换，然后进行回归，建立如下形式的方程：

[f（x）=wTφ（x）+b] （6）

采用式（7）对式（6）中的[w]和[b]进行求解：

[minw2+12γi=1nζ2is.t.    yi-wTφ（x）+b=ei] （7）

式中：[γ]表示正则化参数;[ζi]表示松弛因子;[ei]为回归误差[14?15]。

由于式（7）求解比较复杂，引入拉格朗日乘子[αi]建立拉格朗日乘函数，即：

[L（w，b，ζ，α）=12wTw+12γi=1nζ2i+i=1nαi（wTφ（xi）-b+ζi-yi）]   （8）

对式（8）求偏导数，并且设置条件[?L?w=0，?L?b=0，][?L?ξi=0，?L?αi=0]，可以得到相应的约束条件为：

[w=i=1nαiφ（xi）i=1nαi=0wφ（xi）+b+ξi-yi=0] （9）

定义[K（xi，xj）=φT（xi）φ（xj）]，那么得到最小二乘支持向量机的回归形式为：

[f（x）=i=1nαiK（xi，xj）+b] （10）

选择径向基核函数为[K（xi，xj）]，具体为：

[K（xi，xj）=exp-xi-xj22σ2 ] （11）

式中[σ]为核宽度参数。

1.3  大数据背景下的电子商务客户流失量预测步骤

大数据背景下的电子商务客户流失量预测步骤如下：

Step1：从电子商务网站上对客户流失量数据进行统计，建立电子商务客户流失量建模的样本集合，主要包括训练样本集合和验证样本集合。

Step2：采用模糊聚类分析算法对电子商务客户流失量预测的训练样本进行处理，只选择与选择样本相关的样本作为新的训练样本集合，将一些无关的样本删除，减少训练样本集合的规模。

Step3：采用最小二乘支持向量机对模糊聚类分析算法处理后的训练样本进行学习，通过10折交叉验证法计算电子商务客户流失量预测精度，根据精度确定最优的参数，从而建立电子商务客户流失量预测模型。

Step4：采用验证样本集合对电子商务客户流失量预测模型的有效性进行测试，并分析电子商务客户流失量预测精度。

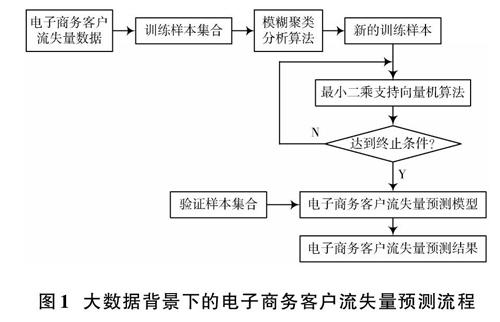
综上可知，基于大数据背景下的电子商务客户流失量预测流程如图1所示。

2  电子商务客户流失量的实证分析

2.1  电子商务客户流失量的历史数据

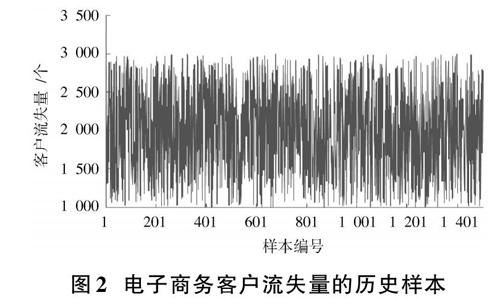
为了分析本文提出的大数据背景下的电子商务客户流失量预测模型的性能，采集一段时间的电子商务客户流失量，如图2所示。从图2可以看出，电子商务客户流失量的随机波动性比较大，为了使电子商务客户流失量预测结果具有说服力，共进行5次仿真实验，每一次随机选择1 000个数据作为电子商务客户流失量建模的训练样本，其余为电子商务客户流失量预测的验证样本，这样每一次仿真实验的具体样本是不一样的。在相同实验条件下，选择决策树的电子商务客户流失量模型、BP神经网络的电子商务客户流失量进行对比测试。

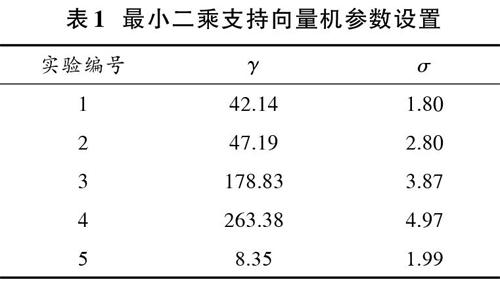
每一次电子商务客户流失量建模实验的最小二乘支持向量机参数设置如表1所示。

2.2  电子商务客户流失量的单步预测精度对比

统计三种模型的电子商务客户流失量的单步预测精度，结果如图3所示。从图3可以看出，三种模型的电子商务客户流失量单步预测精度均较高，可以对电子商务客户流失量变化特点进行描述，但是，相同实验编号下，本文的电子商务客户流失量预测效果更优，预测精度均达到了95%以上。

2.3  电子商务客户流失量的多步预测精度对比

在实际应用中，由于电子商务客户流失量预测要把握将来一段时间的客户流失变化趋势，单步预测的时间太短，没有什么实际应用价值，因此统计三种模型的电子商务客户流失量的多步预测精度，结果如图4所示。从图4可以看出，电子商务客户流失量多步预测精度明显低于单步预测精度，电子商务客户流失量预测误差明显增加，尤其是决策树的电子商务客户流失量预测精度下降的幅度相当大，而本文模型的电子商务客户流失量预测精度仍然很高，相对于对比模型，本文模型的电子商务客户流失量预测结果的优越性十分显著。

2.4  电子商务客户流失量模型的工作效率对比

统计三种模型的电子商务客户流失量建模时间，具体如表2所示。从表2可以看出，决策树和BP神经网络的电子商务客户流失量建模时间明显多于本文模型，本文模型可获得较高的电子商务客户流失量建模效率。

3  结  语

电子商务客户流失量预测是当前的一个研究热点，为了减少电子商务客户流失量预测误差，设计了大数据背景下的电子商务客户流失量预测模型。首先采用模糊聚类分析算法对电子商务客户流失量数据进行预处理，减少电子商务客户流失量预测的训练样本规模;然后采用最小二乘支持向量机建立电子商务客户流失量预测模型。预测结果表明，本文提出的电子商务客户流失量预测模型预测精度高、效率高。

参考文献

[1] 于小兵，王旭明.影响电子商务客户流失因素分析[J].数学的实践与认识，2014，44（21）：1?5.

[2] 于小兵，曹杰，张梦男.B2C电子商务客户流失原因评估研究[J].模糊系统与数学，2012，26（6）：166?172.

[3] 代逸生，沈培兰，孙红霞.基于Pareto/NBD模型的电子商务网站客户流失预测研究[J].科学技术与工程，2010，10（27）：6792?6795.

[4] 李婷婷.影响B2C电子商务企业客户流失因素的实证分析[J].对外经贸，2014（1）：136?137.

[5] 任剑锋，张新祥.电子商务客户流失的建模与预测研究[J].计算机仿真，2012，29（5）：363?366.

[6] 朱帮助，张秋菊，邹昊飞，等.基于OSA算法和GMDH网络集成的电子商务客户流失预测[J].中国管理科学，2011，19（5）：64?70.

[7] 张秋菊，朱帮助.基于自组织数据挖掘的电子商务客户流失预测模型[J].企业经济，2011（1）：95?99.

[8] 张秋菊，朱帮助.基于自组织模糊规则归纳的电子商务客户流失预测[J].计算机应用与软件，2010，27（12）：44?47.

[9] 许宁，高飞.无线网络电子商务客户流失预测仿真[J].计算机仿真，2018，35（9）：475?479.

[10] 武小军，孟苏芳.基于客戶细分和AdaBoost的电子商务客户流失预测研究[J].工业工程，2017，20（2）：99?107.

[11] 于小兵，卢逸群.电子商务客户流失预警与预测[J].系统工程，2016，34（9）：37?43

[12] 琚春华，卢琦蓓，郭飞鹏.融入个体活跃度的电子商务客户流失预测模型[J].系统工程理论与实践，2013，33（1）：141?150.

[13] 杨力.基于在线序列优化极限学习机的电子商务客户流失量预测模型[J].南京理工大学学报，2019，43（1）：108?114.

[14] 卓涛.基于粒子群优化支持向量机的电子商务客户流失预测模型[J].农业网络信息，2014（6）：88?91.

[15] 朱帮助.基于SMC?RS?LSSVM的电子商务客户流失预测模型[J].系统工程理论与实践，2010，30（11）：1960?1967.