基于迭代自适应方法的柱面共形阵2D DOA估计
张状和 韩东 刘德亮

摘 要: 针对柱面共形阵的二维波达方向(2D DOA)估计问题,提出一种基于迭代自适应方法的柱面共形阵2D DOA估计算法。首先,通过欧拉旋转变换公式将柱面共形阵全局直角坐标系变换为单元局部直角坐标系,建立柱面共形天线阵列流型;然后,将感兴趣区域内信号源所有可能存在的位置通过划分二维网格的形式来表示,利用迭代自适应算法(IAA)估计出每个潜在位置对应的信号源能量;最后,绘制能量谱图,谱峰对应的方位角和俯仰角即为二维波达方向的估计值。理论分析与仿真实验证明,所提算法不需要额外的参数匹配,简化了估算步骤,在短快拍的情况下可以实现柱面共形阵的2D DOA估计。
关键词: 柱面共形阵; 2D DOA估计; 坐标系变换; 信号源能量估计; 迭代自适应算法; 能量谱绘制; 理论分析
中图分类号: TN911.7?34 文献标识码: A 文章编号: 1004?373X(2020)11?0006?04
Cylindrical conformal array′s 2D DOA estimation based on iterative adaptive approach
ZHANG Zhuanghe, HAN Dong, LIU Deliang
(Department of Missile Engineering, Army Engineering University of PLA (Shijiazhuang Campus), Shijiazhuang 050003, China)
Abstract: An iterative adaptive approach (IAA) based 2D DOA (two dimensional direction of arrival) estimation algorithm for cylindrical conformal array is proposed to deal with the problem of 2D DOA estimation of cylindrical conformal array. The global rectangular coordinate system of the cylindrical conformal array is transformed into the unit local rectangular coordinate system by Euler rotation transformation formula for the establishment of array manifold of the cylindrical conformal antenna array. All possible locations of signal source in the ROI (region of interest) are represented by dividing 2D grids, and the IAA is used to estimate the signal source energy corresponding to each potential location. An energy spectrum map is drawn, and the azimuth angle and pitch angle corresponding to the spectrum peak are the estimated values of the 2D DOA. Theoretical analysis and simulation experiments prove that it is unnecessary to match additional parameters in the application of the proposed algorithm, so the steps of estimation is simplified and 2D DOA estimation of cylindrical conformal array can be realized under the condition of short snapshot.
Keywords: cylindrical conformal array; 2D DOA estimation; coordinate system transformation; signal source energy estimation; iterative adaptive approach (IAA); energy spectrum drawing; theoretical analysis
0 引 言
共形陣天线是一种和载体外形保持一致的天线[1],其能够和物体结构相融合,可以满足飞机、导弹、卫星等飞行器的隐身和空气动力学需求,有效减少了荷载的大小和重量。相对于传统的线阵和平面阵,共形阵天线还具有覆盖范围大、易伪装、抗干扰能力较强等特点。近些年来,学者们围绕着共形阵列展开了多方面的研究[2?7],其中,由于波达方向(Direction of Arrival,DOA)估计技术在通信、雷达、声呐等领域的重要作用,因此如何实现共形阵列DOA估计受到广泛关注。
文献[2]研究了多重信号分类(Multiple Signal Classification,MUSIC)算法在共形天线中的应用。文献[3]通过虚拟阵列变换技术,应用旋转不变性技术估计信号参数(Estimation of Signal Parameters Via Rotational Invariance Techniques,ESPRIT)和MUSIC算法,克服了共形载体的遮蔽效应,实现了基于共形阵的2D DOA(Two Dimensional Direction of Arrival,2D DOA)估计。但是以上算法忽略了载体曲率对方向图综合的影响,简化了阵列流型的数据模型。文献[4?5]通过运用欧拉旋转变换公式,提出了共形天线阵列流型的通用建模方法。文献[6]通过合理设置阵元,并基于ESPRIT,解决了柱面共形阵的盲极化2D DOA估计。文献[7]则引入了虚拟期望信号,利用最大信干噪比准则下的最优权矢量对接收信号进行加权处理,实现了共形阵DOA估计。上述文献均将经典的子空间类算法应用到了共形阵列DOA估计问题上,但是这些算法都需要大量的快拍数据支撑,以保证对样本协方差矩阵进行特征分解时,信号子空间与噪声子空间不发生混叠,同时获得高精度、高分辨率的估计结果。但是在实际的工程应用中,信号经常处于不能长时间稳定或快速时变的环境中,如高速目标追踪、水下信号处理、城市无线通信等,采集大量的快拍数据会导致处理时间过长,增大与真实样本的误差或降低运算速度等问题。而近些年来,随着稀疏信号处理理论的兴起,尤其以Petre Stoica等提出的振幅和相位估计的迭代自适应方法(Iterative Adaptive Approach for Amplitude and Phase Estimation, IAA?APES)[8?9]、基于协方差稀疏迭代的谱估计方法(Sparse Iterative Covariance?based Estimation Method, SPICE)[10]为代表,使得短快拍DOA估计的实现成为可能。
为了能在短快拍条件下实现共形阵列天线的高精度2D DOA估计,本文提出了一种基于迭代自适应方法的柱面共形阵2D DOA估计算法。首先,利用欧拉旋转变换公式,实现柱面共形阵天线全局直角坐标系到单元局部直角坐标系的变换,建立柱面共形天线阵列流型;然后,基于加权最小二乘法估计出入射信号源的能量,通过循环迭代对估计结果进行更新直至收敛;最后,绘制出三维能量谱图,谱峰对应方位角和俯仰角即为入射信源的2D DOA。仿真实验表明,在只有2个快拍的情况下,所提算法经过适量迭代就能实现对入射信号源2D DOA的高精度、高分辨率估计。
下面对文中的符号和算子进行说明:[[?]*]表示复数共轭;[[?]T]表示转置;[[?]H]表示共轭转置;[?]表示克罗内克积;[x]表示[x]的估计值;[diag(? )]表示对角化;[E[?]]表示期望值;[?]表示Euclidean范數。
1 柱面共形阵数据模型
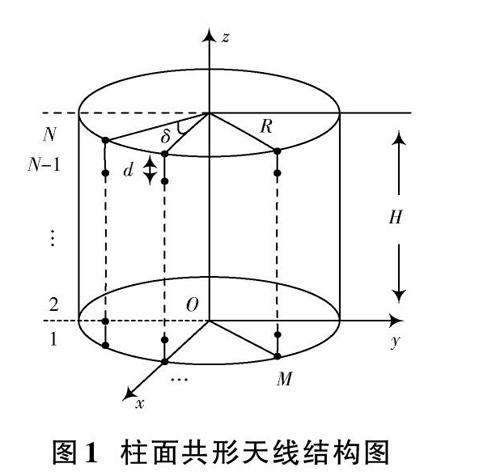
柱面共形阵列天线结构如图1所示。[M×N] 个阵元均匀地分布在载体表面,定义[n]为由下至上的阵元序号,[m]为每一圆环上逆时针方向的阵元序号,[R]表示圆柱半径,[H]表示圆柱的高,[d]为上下两阵元间的距离,[β] 为相邻两阵元间的夹角,[?]为圆环末阵元与[x]轴的夹角;并定义坐标系[[x,y,z]]表示阵列全局直角坐标系,[[x,y,z]] 表示阵元局部直角坐标系,[[r,θ,φ]]表示阵列全局极坐标,[[r,θ,φ]]表示阵元局部极坐标。
给出阵元坐标以及欧拉旋转变换角公式[4]:
[xnm=Rcos[(m-1)β-?]] (1)
[ynm=Rsin[(m-1)β-?]] (2)
[znm=nd-(N+1)d/2] (3)
[Dnm=π-?+(M-1)βEnm=-π2Fnm=0] (4)
假设有[K]个远场窄带信号源入射到图1所示柱面共形阵上,[θi],[?i]分别表示第[i]个入射信号源的方位角与俯仰角,结合文献[4?5],柱面共形阵的导向矢量模型可以表示为:
[a(θ,?)=[r1e-j2πp1?uλ,r2e-j2πp2?uλ,…,rNMe-j2πpnm?uλ]T] (5)
[ri=(g2iθ+g2i?)12(k2iθ+k2i?)12cos θigk=giplcos θigk=gi?pl=giθkθ+gi?k?] (6)
式中:[pnm=[xnm,ynm,znm]]([n=1,2,…,N],[m=1,2,…,M])表示第[nm] 个阵元的坐标矢量;如图2所示,[u=[cos θsin ?,sin θsin ?,cos ?]T]定义为传播矢量;[ri]表示第[i]个阵元对单位信号的响应;[gi]为阵元方向图表达式;[giθ,gi?]分别由信源构成的矢量基[uθ,u?]所构成;[θigk]为[gi]和[pl]向量之间的夹角。
考虑到入射信号源均相互独立,噪声为加性高斯白噪声,因此快拍数据模型可以表示为:
[X(n)=AS(n)+N(n)] (7)
[S(n)=[s1,s2,…,sn]T] (8)
[N(n)=[n1,n2,…,nn]T] (9)
[A(θ,?)=[a(θ1,?1),a(θ2,?2),…,a(θNM,?NM)]] (10)
式中:[A(θ,?)]表示导向矩阵,由导向矢量构成;[S]表示信号矢量;[N]表示加性高斯白噪声矢量。通常情况下,实际感兴趣的目标信号源数大于扫描区域内信号源的个数,导致[S(n)]中只有一小部分的数值是非零的,因此稀疏类算法适用于DOA估计。
2 柱面共形阵2D DOA估计算法
首先,构造[K×K]的能量矩阵[P],其对角线元素包含了扫描网格上每个角度的信号能量。能量矩阵的结构如下:
[P=diag{p1,p2,…,pi}] (11)
[pi=1Nn=1Nsi(n)2, i=1,2,…,K] (12)
定义噪声和干扰的协方差矩阵如下:
[Q(θi,?i)=R-pia(θi,?i)aH(θi,?i)] (13)
式中[R=A(θ,?)PAH(θ,?)]。
加权最小二乘法的代价函数由下式给出:
[n=1Nx(n)-si(n)a(θi,?i)2W] (14)
式中:[y2W=yHWy];[si(n)]是第[i]个远场信号源在快拍数[n]处的复幅值;[Q-1(θi,?i)]是噪声的协方差矩阵,由文献[7]可知,当[W=Q-1(θi,?i)]时[si(n)]的值取最小,因此,对式(14)求关于[si(n)]的最小化,表达形式为:
[si(n)=aH(θi,?i)Q-1(θi,?i)x(n)aH(θi,?i)Q-1(θi,?i)a(θi,?i), n=1,2,…,N] (15)
式中:[Q-1(θi,?i)]可由[R-1]代替,式(15)可以精简为:
[si(n)=aH(θi,?i)R-1x(n)aH(θi,?i)R-1a(θi,?i), n=1,2,…,N] (16)
式(16)得到了[(θi,?i)]处对应信源复幅值的估计值。将[si(n)]代入式(12)即可计算第[i]个扫描点的能量。
算法流程总结如下:
初始化:
[s(0)i(n)=aH(θi,?i)x(n)a(θi,?i)2, i=1,2,…,K] (17)
[p(0)i=1Nn=1Ns(0)i(n)2, i=1,2,…,K] (18)
[P(0)=diag{p(0)1,p(0)2,…,p(0)K}] (19)
迭代过程如下:
1) 构造能量矩阵[p(l)i=1Nn=1Ns(l-1)i(n)2],[i=1,][2,…,K];[p(l)i]是第[i]个网格点对应的信号源在第[l]次迭代的能量估计值。
2) 计算信号协方差矩阵[R=A(θ,?)P(l)AH(θ,?)]。
3) 更新[s(l)i(n)=aH(θi,?i)R-1x(n)aH(θi,?i)R-1a(θi,?i)]。
4) 当迭代收敛,则停止迭代,否则返回式(1),根据经验,一般迭代10~15次就会得到较好的估计值。
计算能量值:迭代结束后,以最后一次迭代得到的[p(end)i]作为第[i]个扫描点对应的谱峰函数绘制出三维谱峰图,谱峰对应的方位角、俯仰角即为真实信源的二维波达角度。
3 仿真实验与分析
为验证本文所提方法的有效性,对比2D?MUSIC算法展开实验。为了不失一般性,设置如图1所示的接收阵列,[M=5],[N=10],相邻两圆环的间距为入射信号波长的一半,即[d=λ/2];噪声为加性高斯白噪声,与入射信号源相互独立;信号源个数[K=2],且相互独立;[θ1=55°],[?1=30°],[θ2=60°],[?2=35°];假设在DOA估计之前已对感兴趣的区域有一定认知,所以提前设定方位角度扫描范围为[[50°,65°]],俯仰角度扫描范围为[[25°,40°]],扫描间隔为[0.5°];迭代次数预设[l=10]。单元方向图设置为[4]:
当[0≤θ≤π2]时:
[gθ(θ,?)=J2πdλsin θ-J0πdλsin θ×(cos ?-jsin ?)] (20)
[g?(θ,?)=J2πdλsin θ+J0πdλsin θ×cos θ(sin ?-jcos ?)] (21)
其他时,
[gθ(θ,?)=g?(θ,?)=0]
式中[J0,J2]分别是零阶和二阶第一类贝塞尔函数。
3.1 仿真实验1
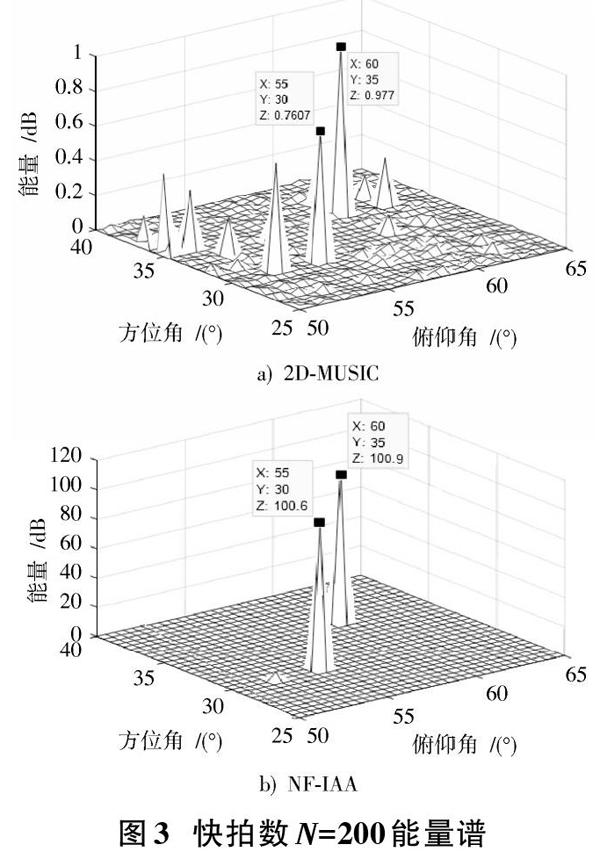
设置信噪比(Signal to Noise Ratio,SNR)为15 dB,快拍数[N1=2,N2=200],能量谱分别如图3,图4所示。
图3,图4仿真结果表明,当快拍数足够大时,两种算法都能成功地把三个近场信源分辨出来;而当快拍数减小到[N1=2] 时,2D?MUSIC算法已经失效,真实信号源的谱峰混叠在伪峰之中,已无法分辨出真实入射角度,但所提算法仍然可以分辨出两个锐利的谱峰,且旁瓣水平较低,方位角和俯仰角的估计偏差也很小。
3.2 仿真实验2
定义实验成功须满足下式:
[(θ)-θ≤3°, (?)-?≤3°] (22)
图5设置快拍数[N2=200],信噪比从-15 dB变化到15 dB。图6设置信噪比為10 dB,快拍数从10变化到200,其他实验条件不变。200次蒙特卡洛实验观察分辨概率和均方根误差随快拍数的变化曲线。
从图5的实验结果可以看出,所提算法的估计均方根误差要小于2D?MUSIC算法,说明所提算法的估计精度更高。从图6的实验结果可以看出,当快拍数大于70时,所提算法的分辨概率趋于100%,而2D?MUSIC算法的分辨概率依旧很低。
4 结 语
针对柱面共形阵的2D DOA估计问题,提出一种基于IAA的估计算法。本文利用欧拉旋转变换公式,将柱面共形阵天线全局直角坐标系变换到单元局部直角坐标系,讨论了稀疏类算法在DOA估计应用上的原理,使用IAA算法解决了短快拍条件下的柱面共形阵的2D DOA估计问题,计算机仿真验证了所提算法的有效性。
参考文献
[1] JOSEFSSO L, PERSSON P. Conformal array antenna theory and design [M]. New Jersey: John Wiley & Sons, Inc., 2006.
[2] 孙翠珍,毛昕蓉.多重信号分类算法在共形阵列天线中的应用[J].计算机仿真,2014,31(11):171?174.
[3] 王瑞革,王法栋.基于虚拟阵列变换的共形阵列信号DOA估计[J].雷达科学与技术,2016,14(4):448?452.
[4] 王布宏,郭英,王永良,等.共形天线阵列流形的建模方法[J].电子学报,2009,37(3):481?484.
[5] 李龙军,王布宏,夏春和.稀疏共形阵列天线方向图综合[J].电子学报,2017,45(1):104?111
[6] 张羚,郭英,齐子森,等.柱面共形阵列天线盲极化2D DOA估计[J].空军工程大学学报(自然科学版),2016,17(3):78?84.
[7] 杨群,曹祥玉,高军,等.一种未知信源数的共形阵DOA算法[J].西安电子科技大学学报(自然科学版),2015,42(3):122?128.
[8] YARDIBI T, LI J, STOICA P, et al. Source localization and sensing: a nonparametric iterative adaptive approach based on weighted least squares [J]. IEEE transactions on aerospace and electronic system, 2010, 46(1): 425?443.
[9] STOICA P, LI J, HE H. Spectral analysis of nonuniformly sampled data: a new approach versus the periodogram [J]. IEEE transactions on signal processing, 2009, 57(3): 843?858.
[10] STOICA P, BABU P, LI J. New method of sparse parameter estimation in separable models and its use for spectral analysis of irregularly sampled data [J]. IEEE transactions on signal processing, 2011, 59(1): 35?47.

