基于通视性算法的卫星动中通阴影问题分析
李易依 贾维敏 戴精科


摘 要: 为了进行卫星动中通阴影问题分析,针对传统的JANUS通视性算法存在准确度不高的问题,提出一种改进的JANUS通视性算法。该方法建立了基于地球坐标系的通视性数学模型,并通过缩短步长增加检查点的数量。仿真实验结果表明,改进的JANUS通视性算法有效克服了地球曲率的影响,算法的准确度得到了大幅度提升,通视性判断结果可以为卫星动中通用户规划行驶路线提供参考,为下一步开发卫星动中通路径导航系统提供了理论支撑。
关键词: 卫星动中通; 通视性数学模型; JANUS算法; 阴影遮挡; 地球坐标系; 地球曲率
中图分类号: TN927?34; TP391.9 文献标识码: A 文章编号: 1004?373X(2020)11?0001?05
Analysis of shadow problem existing in SOTM?based visibility algorithm
LI Yiyi, JIA Weimin, DAI Jingke
(Rocket Force University of Engineering, Xian 710025, China)
Abstract: In view of the low accuracy in the traditional JANUS visibility algorithm, an improved JANUS visibility algorithm is proposed to analyze the shadow problem existing in satcom?on?the?move (SOTM). In the algorithm, a visibility mathematical model based on the earth coordinate system is established, and the number of checkpoints is increased by shortening the step size. The results of simulation experiment show that the improved JANUS visibility algorithm can effectively overcome the influence of the earth curvature, and the accuracy of the algorithm has been greatly improved. The results of the visibility judgment can provide a reference for SOTM users to plan their driving routes and theoretical support for the development of SOTM path navigation system.
Keywords: SOTM; visibility math model; JANUS algorithm; shadow occlusion; earth coordinate system; earth curvature
0 引 言
卫星动中通是指运动中的卫星通信系统,即将卫星通信地面站安装在车辆、轮船、飞机等移动载体上,在载体运动过程中使天线波束时刻指向目标卫星,不间断地传递语音、数据、图像等多媒体信息。它具有覆盖区域广、通信距离远、信道容量大、网络部署快速、机动、灵活等特点,已经成为当前卫星移动通信研究和应用的热点领域[1?2]。卫星动中通工作频段在Ku及以上波段,属于视线传播,运动过程中遇到桥梁、高山、高大建筑物等受到遮挡导致通信中断是客观规律[3]。但是,如果使用者不知道当前通信已经中断,仍然继续传输信息则会造成信息丢失或者网络通信拥塞等问题,因此卫星动中通通信链路的阴影遮挡是一个至关重要的问题[4]。对于卫星动中通使用者而言,迫切需要预先掌握当前整条行驶路段的通信路况,以保证信息可靠的传输[5]。
目前,国内外对动中通阴影研究的重点是实时、可靠地检测阴影,及驶出阴影后的快速再捕获问题。如文献[4]使用链路预算的方法,将卫星信标信号作为阴影的判决标准,当接收到目标卫星的信标信号,表明天线波束对准目标卫星或者处在目标卫星附近,否则表明受到了阴影遮挡。但该方法只在当卫星动中通已经进入受阴影遮挡的区域后给出受遮挡的判断结果,一旦阴影消失,则迅速恢复通信,但是何时恢复通信,行驶过程中还有哪些路段可能受到阴影遮挡,这些信息用户均无法提前获知。因此,用户因无法预知当前行驶路段的通信链路状态,即不知道哪部分是通信畅通路段,哪部分是阴影遮挡路段,导致传输信息存在较大的盲目性。若动中通在通信畅通路段,信息可以可靠传输;若在阴影遮挡路段则信息无法传输到对方,可能会造成信息堵塞。如果已经提前计算出行驶路段的通信状况,并将该信息预先存储到动中通通信路径导航系统中,那么用户就可以像平时生活中使用地图导航系统一样,可以提前筹划传输信息的时机,从而保证信息传输的可靠性。若出发地与目的地存在多条道路,用户可以根据各道路的通信状况提前进行路径规划,优先选择通信状况更佳的路径。为此,本文研究的重点是动中通所在位置与卫星的通视情况。
为了有效确定卫星动中通在某条道路上或某一区域内的阴影状态,本文采用通视性分析(Visibility Analysis)技术判断卫星动中通与卫星之间是否受到地形的遮挡。传统的通视性算法如DYNTACS通视性算法、JANUS通视性算法等,大都是基于通视点所在平面建立的三维直角坐标系实现通视性的判断[6],由于地球曲率的影响,将地球表面简化為二维平面所带来的误差会随着地形范围的扩大不断增大,而卫星动中通具有运动区域广、通信距离远等特征,传统的通视性算法不再适用于判断卫星动中通与卫星之间的通视性。为此,本文对传统的JANUS通视性算法加以改进,最后将改进的JANUS通视性算法应用于预测卫星动中通在某条道路上或某一区域内的阴影状态。
1 基于地球坐标系的通视性数学模型
1.1 数字地形模型
数字地形模型(Digital Terrain Model,DTM)是描述地球表面形态多种信息空间分布的有序数值阵列,可以用下述二维函数系列取值的有序集合来概括地表示数字地形模型的丰富内容和多样形式:
[Kp=f(up,vp), K=1,2,…,m;p=1,2,…,n] (1)
式中:[Kp]为第[p]号地面点上的第[K]类地面特征信息的取值;[(up,vp)]为第[p]号地面点的二维坐标,可以采用任一地图投影的平面坐标,或者是经纬度和矩阵的行列号;[m]为地面特征信息类型的数目;[n]为地面点的个数。当[K]代表高程信息时,式(1)代表数字地形模型;当[m=1]且[f]为地面高程的映射,[(up,vp)]为矩阵行列号时,式(1)代表DEM。根据分割方法的不同,可以将数字地形模型分为规则方形网格(Regular Square Grid,RSG)模型和不规则三角网(Triangulated Irregular Network,TIN)模型[7]。本文研究的是基于RSG模型的通视性算法。
1.2 通视性概念
通视性问题分为点通视性、线通视性和区域通视性[8],本文中研究的卫星动中通与卫星的通视性是点对点的通视性问题。点对点的通视性就是判断从一点出发能否看到另一点。以车载动中通为例,假定车载动中通为视点[V],则卫星为目标点[T],将视点[V]和目标点[T]的连接线段称为视线(Line of Sight,LOS)。当视线上的任一点都在地形之上时,[V],[T]之间可以通视;否则不可通视。衛星动中通与卫星的通视性模型如图1所示。
1.3 基于大地坐标的通视性数学模型
为了消除传统通视性算法中由于将地球表面简化为二维平面带来的误差,本文将视线上的任意一点在全球统一坐标系中进行描述。以大地坐标系为大地高程的参考坐标系,利用大地坐标系和地心空间直角坐标系之间的转换计算各检查点在视线上的高程,采用插值法求解各检查点在地形上的高程,进而判断视点和目标点之间的通视性。其中,标准椭球采用WGS?84,大地坐标系和地心直角坐标系的转换公式[9]为:
[x=(N+H)cosBcosLy=(N+H)cosBsinLz=[N(1-e2)+H]sinB] (2)
式中:[x],[y],[z]表示地心空间直角坐标系下某点的坐标值;[B],[L],[H]为某点的大地坐标;[e2]为椭球第一偏心率的平方;[N]为纬度[B]处的卯酉圈半径,[N=a1-e2sin2B12],[a=]6 378 137 m,表示地球的长半轴。
视线、地形和地球椭球的截面图如图2所示。其中,[PLOS]为[V?T]视线的任意一点,将该点沿铅垂线方向投影,与地形表面的交点定义为[PT],与地球椭球面的交点为检查点[P],由此可知,三点的经纬度相同,只是高程不相同;其中,[HLOS]表示检查点[P]在视线上的高程,[H]表示检查点[P]在地形上的高程。
2 改进的JANUS通视性算法
2.1 基于大地坐标的JANUS通视性算法
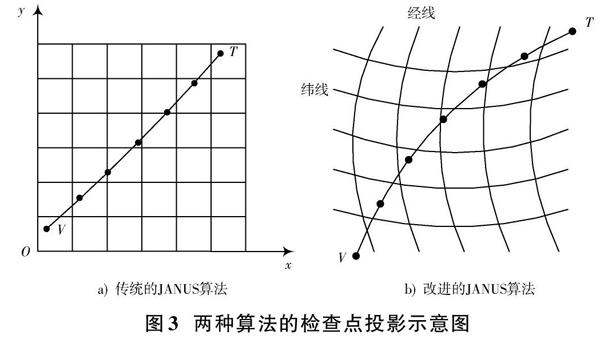
在传统的JANUS算法中,检查点是通过视线在[xOy]平面上的投影直线上等步长计算所得[10]。首先计算视点[V]和目标点[T]之间[x],[y]偏移量,用较大的偏移量除以地形分辨率并取整,即计算出了步长[11],如图3a)所示。本文中的检查点是传统的JANUS算法中的检查点在地球椭球面的投影,如图3b)所示,通过比较检查点在视线上的高程和地形上的高程大小,判断视点和目标点之间的通视性。
1) 计算检查点[P]的经纬度坐标和在视线上点[PLOS]的高程[HLOS]
设视点[V]的地心空间直角坐标和大地坐标分别为[(xV,yV,zV)]和[(LV,BV,HV)],目标点[T]的地心空间直角坐标和大地坐标分别为[(xT,yT,zT)]和[(LT,BT,HT)],[PLOS]的地心空间直角坐标和大地坐标分别为[(xLOS,yLOS,zLOS)]和[(LLOS,BLOS,HLOS)],检查点[P]的经纬度坐标为[(L,B)],地形分辨率为[D],步长为[d]。在地心空间直角坐标系下,视线方程可表示为:
[x-xVxT-xV=y-yVyT-yV=z-zVzT-zV] (3)
已知视点[V]的大地坐标为[(LV,BV,HV)]和目标点[T]的大地坐标为[(LT,BT,HT)]。
利用式(2)将大地坐标转化为空间直角坐标,计算出视点[V]的地心空间直角坐标[(xV,yV,zV)]和目标点[T]的地心空间直角坐标[(xT,yT,zT)]。
步长[d]满足:
[d=maxxV-xT,yV-yTD] (4)
在视线[V?T]上等步长采样并联立式(3),计算各检查点所对应视线上的点[PLOS]的地心空间直角坐标[(xLOS,yLOS,zLOS)]。再利用式(2)将空间直角坐标转换到大地坐标,求得PLOS的大地坐标为[(LLOS,BLOS,HLOS)],其中,[(LLOS,BLOS)=(L,B)]。这样就可以计算所有检查点[P]的大地坐标和在视线上点[PLOS]的高程[HLOS]。
2) 计算点[PT]在地形上的高程[H]
本文所采用的高程数据为DEM数据,根据计算出的[(L,B)]找到与检查点距离最近的4个网格节点的经纬度和高程数据,利用双线性插值法计算得到检查点[P]在地形上的高程[H]。
3) 通视性判断
比较检查点在视线上的高程[HLOS]和地形上的高程[H]的大小,若所有检查点的[HLOS]均大于[H],则判断视点[V]与目标点[T]之间可通视,否则为不可通视。
2.2 增加检查点的数量
在传统的JANUS算法中,视点[V]和目标点[T]之间[x],[y]偏移量中的较大值除以地形分辨率并取整,即计算出了步长,所以在每个单元格中仅取一个检查点,检查点数量较少导致算法准确度不高。为此,本文基于大地坐标的JANUS通视性算法成倍数缩短步长[d],使得检查点的数量相应成倍数增加。使检查点的数量增加1倍的算法示意图如图4所示。
3 仿真实验与结果分析
3.1 仿真1:验证地球曲率对通视性的影响
为了检验基于大地坐标的JANUS通视性算法能否有效克服地球曲率对通视性结果的影响,本文设计以下实验进行验证。为了排除地形因素仅考虑地球曲率的影响,本实验中构建一个WGS?84椭球体形状的表面高程全为0的地球理想模型。设定视点[V]的大地坐标为(109.50°E,34°N,100 m),设定目标点[T]的经度为109.50°E,高程为0。通过改变目标点的纬度,控制视线所跨范围的大小,进而比较在不同地域跨度条件下传统的JANUS通视性算法和基于大地坐标的JANUS通视性算法的通视性检查结果。计算结果如表1所示,其中,“1”表示可以通视,“0”表示不可通视, 符号[dVT]表示视点和目标点之间的直线距离,单位为km。DEM数据为精度是30 m。
分析表1中的结果可知,随着视点与目标点之间距离的增大,视线所跨的地域范围随之增大。利用传统的JANUS通视性算法计算所得的通视性结果始终为“1”,这是因为在地球表面高程全为0的理想条件下,传统的JANUS通视性算法中将球面投影到[xOy]平面,那么以[xOy]平面为高程参考面时的高程也均为0。又因为视点[V]的高程为100 m,目标点[T]的高程为0,两点之间存在高程差,所以无论视线所跨地域范围扩大或缩小,传统的JANUS通视性算法的通视性检查结果均为可以通视,如图5所示。
而利用基于大地坐标的JANUS算法时,当视点与目标点之间的距离小于35.091 km时,计算所得的通视性结果为“1”;当视点与目标点之间距离大于或等于35.091 km时,计算所得的通视性结果为“0”。如图6所示,将地球模型简化为半径[R]为6 371 km的球体,[O]点为地心,[Q]点为从视点[V]出发的视线刚好与地球表面相切的点,[h]为视点[V]的高程。利用公式[(R+h)2-R2]计算可得[V]点和[Q]点之间的距离约为35.696 km。由图6易知,当目标点[T]位于[Q]点左侧,即[V]与[T]之间的距离小于35.696 km时,[V]与[T]之间可以通视;当目标点[T]位于[Q]点右侧,即[V]与[T]之间的距离大于35.696 km时,[V]与[T]之间不可通视。仿真结果与理论结果一致。
经过以上仿真实验有效验证了基于大地坐标的JANUS算法可以有效克服地球曲率的影响,然后在真实的地形上进行实验。
3.2 实验2:对实际地形进行通视性计算
实验区域选在陕西西安附近边长为70 km的方形区域,目标卫星为亚太五号,其大地坐标为(138.0°E,0°N,36 000 km),在实验区域内随机选取500个视点。得到改进的JANUS通视性算法在不同地形分辨率下的通视性计算结果,如表2和表3所示,其中,[n]为检查点数量增加的倍数,时间为500个点对的总计算时间。
分析表2和表3中的数据可知,当[n]值固定时,地形分辨率越高,可通视点对的数量越少,计算时间越长;当地形分辨率固定时,[n]值越大,可通视点对的数量越少,计算时间越长。为了更直观地对比计算结果,将表做成二维曲线图如图7所示。
由图7a)可知,通过增大[n]值可以使算法在较低地形分辨率计算所得的准确度达到在较高地形分辨率计算所得的准确度,且当[n>10]之后,可通视点对的数量变化趋于平缓。由图7b)可知,计算时间随着[n]值的增大成线性增大的趋势,因此取[n=10]。以传统的JANUS通视性算法在30 m地形分辨率下的计算结果为参照,将当[n=10]时,改进的JANUS通视性算法在不同地形分辨率下的准确度和计算时间与之相比,对比结果如表4所示。
分析表4结果可得,与传统算法相比,随着地形分辨率的增加,改进算法的准确度提高值越来越大,而算法的效率越来越低,这是因为地形分辨率越高计算量越大,与客观规律相符。而本文研究的目的是利用通视性算法进行卫星动中通阴影问题分析,预先计算出行驶路段的通信状况,然后将该信息预先存储到动中通通信路径导航系统中,并没有实时性的要求,对算法的准确度要求较高,而对计算效率没有过高的要求。
4 结 论
本文对通視性问题进行了理论分析和实验仿真,发现传统的JANUS通视性算法没有考虑地球曲率的影响,仅适用于小范围内的地形通视性结果计算,不适用于覆盖区域广、通信距离远的卫星动中通的阴影问题分析,并且由于检查点数量较少导致算法准确度不高。针对以上问题,本文提出了一种改进的JANUS通视性算法。仿真实验结果表明,本文提出的改进JANUS通视性算法不仅有效考虑了地球曲率的影响,并且在算法的准确度上有明显的优越性,可以用于预测卫星动中通在某条道路上或某一区域内的通信状态,为动中通用户合理规划路径,提前筹划信息传输的时机提供了可靠的理论依据。
参考文献
[1] IPPOLITO L J, Jr.卫星通信系统工程[M].北京:国防工业出版社,2012.
[2] 杨新华,刘杨,雷迪伟.动中通卫星通信系统链路预算及实例分析[J].通信技术,2018,51(1):24?29.
[3] 丁玲.“动中通”卫星转播系统线路保障方法研究[D].大连:大连理工大学,2016.
[4] 王冬.卫星链路预算问题的相关研究[D].西安:西安电子科技大学,2017.
[5] 刘杉,贾维敏,吴诗琪,等.基于地理信息的动中通阴影判断分析[C]//国家安全地球物理丛书(十二):地球物理与信息感知.北京:中国地球物理学会,2016:848?859.
[6] 李志林,朱庆.数字高程模型[M].武汉:武汉测绘科技大学出版社,2000.
[7] 余文广,李群,侯洪涛.基于大地坐标的通视性检查算法[J].计算机仿真,2008,25(11):28?31.
[8] GOLUB D, DOYTSHER Y, FISHER?GEWIRTZMAN D.3D visibility analysis indicating quantitative and qualitative aspects of the visible space [J]. Survey review, 2017, 50(359): 134?146.
[9] 张万恩,黄然.基于大地坐标系与直角坐标系转换的论述[J].科技经济导刊,2018,26(25):165.
[10] 张飞兰.景观可视性定量计算方法的研究[D].深圳:深圳大学,2015.
[11] 王臣.通视性探测模型研究及其在陆军仿真系统中的应用[D].北京:北京邮电大学,2017.

