全双工无线通信中射频自干扰抑制的凸优化分析

周娟 刘岚 陈超 何梦 沈莹

摘  要： 全双工无线通信网络中，通过有效的自干扰抑制手段，终端设备可以采用同时同频收发的全双工模式工作。文中主要研究的是有用信号对射频域自干扰抑制性能的影响。通过对射频自干扰抑制性能的分析，可以看出，在不存在有用信号的情况下，射频自干扰抑制是一个凸优化问题，可以得到最优估计参数及最佳射频干扰抑制性能。当有用信号存在且信道时变，射频自干扰抑制不再是凸优化问题，自干扰抑制能力下降。实验仿真验证了理论分析结果，进一步表明有用信号的信道条件是限制射频域自干扰抑制性能的重要因素，且在非凸优化情况下，干扰抑制性能恶化。

关键词： 凸优化分析; 无线通信; 全双工模式; 射频域自干扰抑制; 理论分析; 仿真验证

中图分类号： TN92?34                          文献标识码： A                           文章编号： 1004?373X（2020）11?0029?04

Convex optimization analysis of radio frequency self?interference suppression

in full?duplex wireless communication

ZHOU Juan1， LIU Lan1， CHEN Chao1， HE Meng2， SHEN Ying2

（1. College of Communication Engineering， Chengdu University of Information Technology， Chengdu 610225， China;

2. Lab of Anti?interference Communication， University of Electronic Science and Technology of China， Chengdu 611731， China）

Abstract： With the efficient means of self?interference suppression， the terminal equipment in full?duplex wireless communication network is allowed to transmit and receive signals in full?duplex pattern simultaneously in the same frequency band. The effect of useful signals on the self?interference suppression performance of the radio frequency （RF） domain is studied mainly in this paper. By analyzing the performance of RF self?interference suppression， it can be found that， in the absence of useful signals， RF self?interference suppression belongs to a convex optimization category， and the optimal estimation parameters and optimal RF interference cancellation performance can be obtained. However， when the useful signal exists and the channel is time?variant， the RF self?interference suppression is no longer a convex optimization problem， and the self?interference suppression capability is degraded. The theoretical analysis results were verified by both the simulation and the experiment， which further show that the channel condition of the useful signal is an important factor limiting the self?interference suppression performance of the RF domain， and the interference suppression performance is degraded under the condition of non?convex optimization.

Keywords： convex optimization analysis; wireless communication; full?duplex pattern; RF self?interference suppression; theoretical analysis; simulation verification

0  引  言

同时同频全双工通信系统中，无线终端在相同时间、相同频率进行信号收发，产生很强的自干扰。在实际系统中，自干扰成为全双工通信的最大实现障碍之一[1?4]。自干扰抑制通常采用三种方法来实现，包括天线自干扰抑制、射频域自干扰抑制和数字域自干扰抑制[5]。

射频域自干扰抑制作为一种重要的自干扰抑制方法，受到广泛关注。现有文献中，射频域自干扰抑制通常在忽略有用信号的影响下进行研究[6?10]。文献[11]对有用信号进行了分析，但是有用信号对自干扰抑制的影响仅在数字自干扰抑制阶段分析。本文侧重有用信号对射频自干扰抑制凸优化的影响分析。

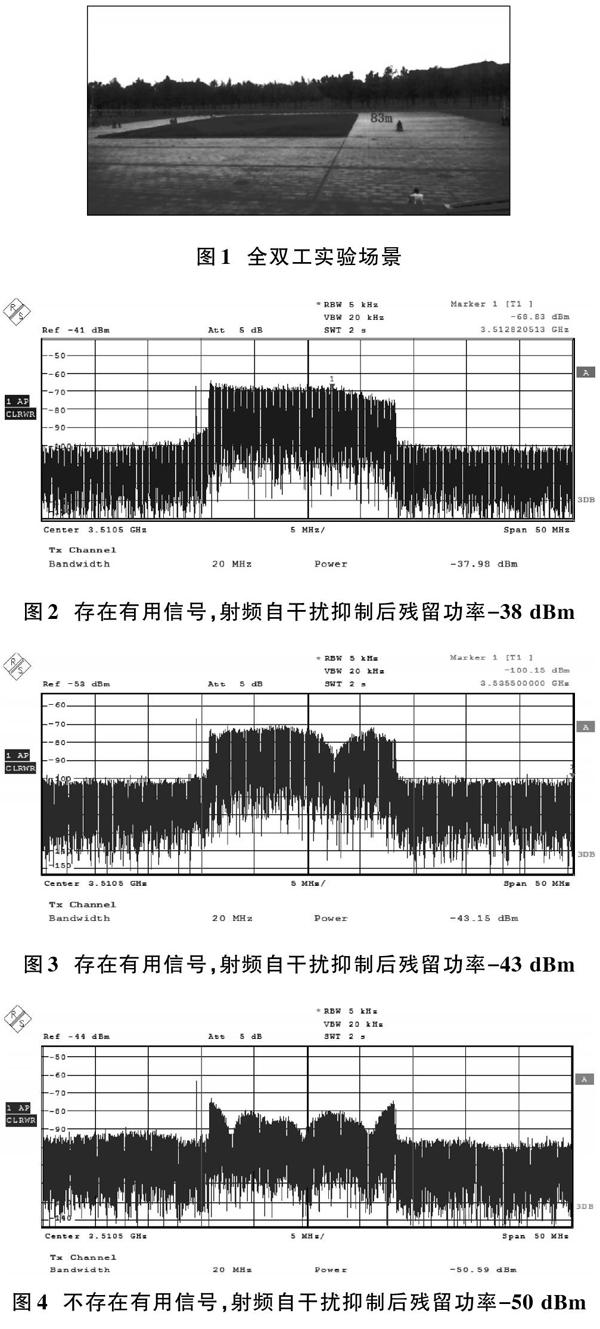
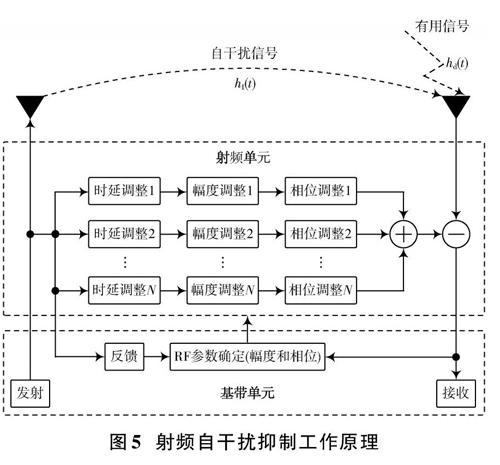
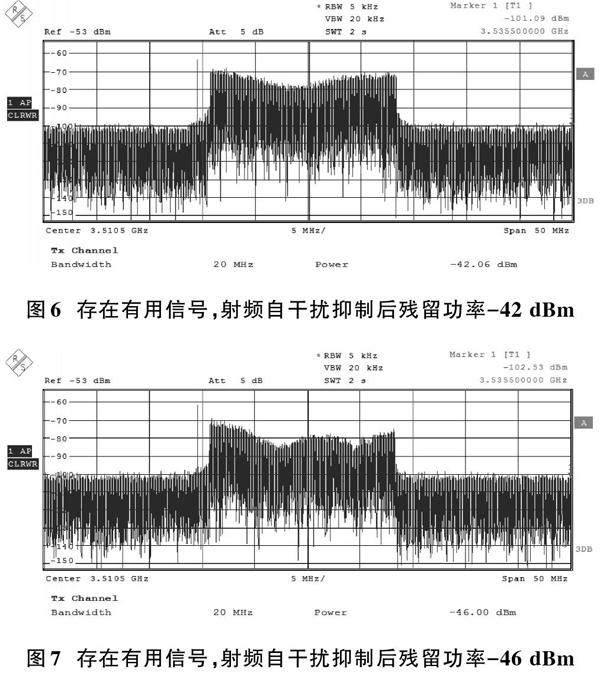
为了分析有用信号的影响，首先建立一个实验平台，以初步观察有用信号对射频域自干扰抑制的影响。该实验场景如图1所示，采用20 MHz带宽的3 GPP LTE协议。其点对点通信距离为83 m，天线增益为6 dBi，发射?接收频率为3.51 GHz，发射功率为32 dBm。如果存在来自远端节点的有用信号，则射频域自干扰抑制的结果有大约5 dB的波动。如图2所示，在最差情况下，自干扰抑制之后的残余信号功率为-38 dBm。如图3所示，在最佳情况下，残余信号功率为-43 dBm。如图4所示，在不存在有用信号的情况下，射频域自干扰抑制结果有小的波动，残余信号功率可低至-50 dBm。

从上述实验结果可以看出，有用信号的存在会对射频自干扰抑制产生影响。接下来，本文将进行数学建模并分析有用信号对射频域自干扰抑制性能的影响。

1  系统模型

系统模型如图5所示，本地终端同时接收来自远程终端的有用信号和本地终端发射天线的自干扰信号。在射频自干扰抑制算法中，首先通过多径估计的方法获得射频域自干扰信号，然后从接收信号中减去估计的射频域自干扰信号。不同的路径具有不同的时延、相位和幅度。

不失一般性的，本地发射信号[x（t）] 可表示为：

[xt=Rebtejωct] （1）

式中：[b（t）]表示通过数模转换器（DAC）后的复基带信号;[ωc]为载波角频率;[Rea]与[Ima] 分别表示[a]的实部与虚部。接收到的自干扰则可相应表示为：

[rxt=i=1NhiRe bt-τiejωct-τiej?i] （2）

式中：[hi，τi，?i]分别代表第[i]条路径的自干扰信道增益、发送时延和相位偏移。令：

[G=h1ej?1h2ej?2…hNej?N] （3）

[D=bt-τ1e-jωcτ1  bt-τ2e-jωcτ2  …  bt-τNe-jωcτNT] （4）

则式（2）可改写为：

[rxt=ReDTGejωct] （5）

为有效进行自干扰抑制，需要估计射频自干扰信号，可由下式描述：

[rxt=k=1KhkRebt-τkejωct-τkej?k] （6）

式中[hk]，[τk]，[?k]分别代表第[k]条路径的自干扰信道增益、发送时延与相位偏移的估计值。[hk]，[?k]的大小在基带单元进行自适应方式估计，而[τk]则通常是通过手动调节电缆长度来改变大小。令：

[Gr=h1ej?1    h2ej?2    …    hNej?N] （7）

[Dr=bt-τ1e-jωcτ1  bt-τ2e-jωcτ2  …  bt-τNe-jωcτNT] （8）

则式（6）可改写为：

[rxt=ReDTrGrejωct] （9）

远端发射信号[s（t）] 也可同样表示为：

[s（t）=Rebs（t）ejωct] （10）

则有用信号可由下式给出：

[rs（t）=m=1MλmRebst-βmejωct-βmejθm] （11）

式中：[λm]，[βm]，[θm]分别表示有用信号的第[m]条路径的信道增益、发送时延和相位偏移。

射频自干扰抑制工作原理如图5所示，射频自干扰被重建并从整个接收信号中减去。

因而，射频自干扰抑制后的残余信号可由下式得出：

[μt=rxt+rst+nt-rt=It+rst+nt] （12）

式中：[n（t）]为白噪声，残余自干扰[It]则为：

[I（t）=Re（DTG-DTrGr）ejωct] （13）

残余信号功率可相应表示为：

[Pr=Eμ（t）2] （14）

由于自干扰信号、有用信号和白噪声彼此独立，所以式（14）可以改写为：

[Pr=PI+Ps+Pn] （15）

残余自干扰信号的功率[PI]为：

[PI=EI（t）2] （16）

而有用信号功率[Ps]为：

[Ps=Ers（t）2] （17）

白噪声功率[Pn]则为：

[Pn=En（t）2] （18）

射频自干扰抑制的目的在于使残余自干扰信号的功率[PI]最小化，即[DTG]應无限近似于[DTrGr]。实际中，先确定每条路径的传输时延[τk]，其在后续的自干扰抑制流程中被固定。为使残余自干扰信号功率[PI]最小化，自干扰信道增益[hk]与相位偏移[?k]在基带单元中实时估计，然而，此时的自干扰信号与有用信号混合在一起，无法分离。因此，用残余接收信号功率[Pr]来代替[PI]，这意味着[hk]与[?k]的估计是基于最小化[Pr]进行的。

2  有用信号对射频域自干扰抑制量的影响

如图5所示，为获得有用信号，首先估计射频自干扰信号，再将其从接收信号中减去，残余接收信号功率为[Pr]，用作确定射频参数的标准。基于[Pr]的最小化，有用信号对射频自干扰抑制的分析如下。

2.1  不存在有用信号

此时有用信号功率[Ps=0]， 残余信号功率[Pr=PI+Pn]。由式（13）、式（16）可知，残余自干扰信号功率可表示为：

[PI=EDTG-DTrGr2] （19）

为方便计算，令：

[DTG=CY] （20）

其中：

[C=ReDT+jImDT-ImDT+jReDT] （21）

[Y=ReG  ImGT] （22）

则残余自干扰信号功率可表示为：

[PIY=ECY-DTrGr2=12ECY-DTrGrHCY-DTrGr=12P0+YHRY-2ReZY] （23）

式中：[P0=EDTGHDTG]为接收自干扰信号功率;[R=ECHC];[Z=GHED*C] 。

因为[R]是自相关且为半正定矩阵，[PI（Y）]在[Y]上是凸的。[Y]表示幅度与相位偏移参数，因而[PI（Y）] 在幅度与相位偏移参数上是凸的。当[Ps=0]，最小化[PI]等效于最小化[Pr]。这意味着可以通过最小化[Pr]来获得最佳幅度和相位偏移。

总的来说，当[Ps=0]时，利用最佳幅度与相位参数[Y*]，残余自干扰信号功率可以最小化[PI，min=PIY*]。

2.2  存在有用信號

[Ps≠0]且[Pr=PI+Ps+Pn]。如果来自远端节点的有用信号的信道增益[λ]是时不变的，由式（11）和式（16）可知，信号功率[Ps]也不变。此时，同样可通过最小化[Pr]来获得最佳幅度与相位。然而，现实中的无线信道常常是时变的，这也就意味着：

[PrY，t=PIY+Pst+Pn] （24）

如果[Ps（t）]是时不变的， 则[PrY，t] 在[Y]上是凸的。如果[Ps（t）]是时变的，则无法保留[PrY] 的凸函数性质。为了便于分析，本文采用梯度下降法来解决最小化问题，搜索方向为负梯度。假设射频自干扰抑制从[t1]时刻开始到[t2]时刻结束，[Yi]表示[Y]在第[i]个维度方向的分量，则[Yi]的搜索方向可通过下式计算：

[Dt≈PrY+κYi，t1-PrY，t2κ=PIY+κYi-PIY+Pst1-Pst2κ=ΔPIκ-ΔPst2-t1κ] （25）

式中：[κ]为步长;[ΔPst2-t1]则表示有用信号的功率差，功率差对抑制射频自干扰的影响分析如下。

在抑制射频自干扰的第一阶段，因为残余自干扰信号的功率远大于有用信号功率，有[PIY?ΔPst2-t1] 。当[κ]的大小合适时，有[ΔPIκ>ΔPst2-t1] ，且[Dt] 的符号不变，从而[PIY]可沿正确方向减少。然而当[PIY]减少到一定程度时，[ΔPIκ] 越来越小。当[ΔPIκ]近似于 [ΔPst2-t1]时，无法保证[ΔPIκ>ΔPst2-t1]，从而[Dt]的符号变得与原来相反。在这种情况下，搜索方向发生错误，[PIY]不会减少。

当存在有用信号时，残余自干扰信号功率可由下式给出：

[PI，s，m=ΔPst2-t1+PI，m] （26）

式中[PI，m]是没有有用信号时的残余自干扰功率的最小值。由式（26）可知，当存在有用信号时，射频自干扰抑制性能随有用信号变化。

3  实验结果

实验平台如图1所示。不存在有用信号的情况下，射频自干扰抑制是一个凸优化问题，能够得到最佳的抑制能力，如图4所示。

为进一步证明理论分析结果，在保持83 m距离的情况下，首先增加通信节点[A]和[B]之间行人或车辆的数量。实验结果表明，射频自干扰抑制波动从5 dB增加到8 dB。这证实了由于有用信号信道条件的较大变化，自干扰抑制凸优化特性被破坏，自干扰抑制能力恶化，与上述理论分析结果一致。

然后将节点[A]和[B]之间的距离增加到150 m，射频自干扰抑制处理之后的频谱如图6，图7所示。可以发现，由于有用信号的平均功率随着距离的增加而减小，距离150 m时的射频自干扰抑制性能优于距离83 m。这是因为有用信号的减少，使得射频自干扰抑制的凸优化特性破坏严重程度削弱。此外，图6和图7中仍然存在射频自干扰抑制波动，因为有用信号通道仍然是时变的，射频自干扰抑制的凸优化特性不能保持。

4  结  语

本文描述了有用信号破坏全双工无线通信系统中的自干扰抑制凸优化特性，从而降低了射频自干扰抑制能力。通过数学推导分析，可以得到残余自干扰信号功率受有用信号功率波动的限制。通过实验仿真验证了理论分析结果。在后续的研究中，减少有用信号对自干扰抑制影响有待进一步讨论。

参考文献

[1] HUA Yingbo， LIANG Ping， MA Yiming， et al. A method for broadband full?duplex MIMO radio [J]. IEEE signal processing letters， 2012， 19（12）： 793?796.

[2] SAHAI A， PATEL G， DICK C， et al. On the impact of phase noise on active cancelation in wireless full?duplex [J]. IEEE transactions on vehicular technology， 2013， 62（9）： 4494?4510.

[3] SABHARWAL A， SCHNITER P， GUO D， et al. In?band full?duplex wireless： challenges and opportunities [J]. IEEE journal on selected areas in communications， 2014， 32（9）： 1637?1652.

[4] SHEN Y， ZHOU J， TANG Youxi. Digital self?interference cancellation in wireless co?time and co?frequency full?duplex system [J]. Wireless personal communications， 2015， 82（4）： 2557?2565.

[5] DUARTE M， DICK C， SABHARWAL A. Experiment?driven characterization of full?duplex wireless systems [J]. IEEE transactions on wireless communications， 2011， 11（12）： 4296?4307.

[6] KORPI D， HEINO M， ICHELN C， et al. Compact inband full?duplex relays with beyond 100 dB self?interference suppression： enabling techniques and field measurements [J]. IEEE transactions on antennas & propagation， 2017， 65（2）： 960?965.

[7] JAIN M， CHOI J II， KIM T， et al. Practical， real?time， full duplex wireless [C]// Proceedings of the 17th Annual International Conference on Mobile Computing and Networking. Las Vegas， Nevada， USA： IEEE， 2011： 301?312.

[8] HE Zhaojun， SHAO Shihai， SHEN Ying， et al. Performance analysis of RF self?interference cancellation in full?duplex wireless communications [J]. IEEE wireless communications letters， 2014， 3（4）： 405?408.

[9] LIU Ying， QUAN Xin， PAN Wensheng， et al. Digitally assisted analog interference cancellation for in?band full?duplex radios [J]. IEEE communications letters， 2017， 21（5）： 1079?1082.

[10] BHARADIA D， MCMILIN E， KATTI S. Full duplex radios [J]. ACM SIGCOMM computer communication review， 2013， 43（4）： 375?386.

[11] KORPI D， ANTTILA L， VALKAMA M. Impact of received signal on self?interference channel estimation and achievable rates in in?band full?duplex transceivers [C]// 2014 48th Asilomar Conference on Signals， Systems and Computers. Pacific Grove， CA， USA： IEEE， 2014： 975?982.