基于沟槽橡胶复合结构的高速列车受电弓隔振降噪研究

曾昭阳，范红伟，焦映厚，李 飞

(哈尔滨工业大学机电工程学院，哈尔滨 150001)

伴随世界经济的不断发展，交通的重要性进一步得到凸显，而高铁属于近些年来发展较快的一种交通工具。当下，中国是全球范围内高铁路线最长、在建工程量最大、发展效率最高的国家。根据官方部门给出的统计资料，截至2015年年底，中国高铁的运营路程超过了1.8万km，在建阶段的总体路线已经达到1万km以上，到2020年，中国的客运专线总里程可望超过2万km。最近的一些研究中观察到，伴随着列车速度的持续提升，其车辆内部噪声不断加大的问题也更加严重[1]。高强度的噪声严重影响乘客的乘坐舒适度，让人产生压力感、疲劳感。造成车内噪声的因素多种多样，比如轮轨激励造成车厢晃动，从而形成辐射噪声。另外高速运行状态下也可能形成空气动力噪声[2-4]。中国的高铁都是通过电力进行牵引，电力提供的主体设备即为布置在车厢上方的受电弓。研究表明，受电弓已成为高速列车的主要噪声源之一[5]。受电弓的噪声产生原因主要包括气动噪声和受电弓振动产生的噪声。目前，针对受电弓降噪研究主要集中在通过优化受电弓的气动外形以降低其气动噪声[6-8]。受电弓在列车运行过程中，在电网弹性不均匀、电缆不平顺、电网波动及气动作用下，会产生不同频率及幅值的振动[9-11]。某高速列车线路运行条件下受电弓区的振动和噪声测试显示，结构振动是该区域噪声传播的重要方式[12]。因此，采用振动隔离技术阻断噪声的传播是降低高速列车受电弓振动噪声的有效措施[13]。

目前，为了减缓振动和降低噪声，橡胶弹性减隔振元件已在中国高速列车上广泛应用，如列车的一系悬挂、二系悬挂等，都运用了专业的弹性元件，从而尽可能实现减振的效果。所运用的橡胶元件和一般的金属弹簧进行比较，其优势众多，比如有助于控制外层摩擦、降低整体的质量、控制噪声、改善舒适性等[14]。因此，针对高速列车的受电弓噪声，利用橡胶复合隔振结构以阻断受电弓振动能量的传递，进而降低受电弓振动引发的车厢内部噪声。首先给出弓网耦合系统对车厢激励的频幅特性，然后研究沟槽橡胶复合隔振结构的动力学响应特点，最后研究沟槽橡胶复合隔振结构的降噪效果。

1 高速列车受电弓激励分析

受电弓即为布置在牵引机车上，经过和接触网保持连接从而得到电能的一类专业性设备。在多年的改进和突破后，现在已经发展为四大种类，比如双臂式、垂直式等，当下中国实际场合中运用最广泛的为单臂受电弓，如图1所示。

图1 高速列车单臂受电弓结构Fig.1 Single-arm pantograph structure of high-speed train

在进行弓网动力学研究时，通常按照动能的等效原理，对受电弓进行简化分析。将其视为具备一定质量的相应模型[15-17]。按照集总质量的状态，此时能够将相应的模型划分成一元、二元等多种形式的模型[18-19]。在进行弓网动力学研究时将受电弓简化为几个二元集中质量模型，如图 2所示。

高速列车取电接触网通常通过定位部件、支持部件等形成。针对接触网，忽略其横向运动，并采用欧拉梁对电缆进行建模，采用弹簧单元对悬吊进行简化。最终，分别基于两自由度受电弓模型以及简化后的接触网模型，相应地创建了弓网耦合体系的研究模型，如图3所示。其中：SA和SB各自对应承力索与接触线的张力；kDi对应第i根吊弦的刚度；ρA与ρB各自对应承力索、接触线的线密度；mDi对应第i根吊弦全部质量的1/2；EIA与EIB对应二者不同的弹性模量；mTAi对应第i根支撑结构的质量；mTBi对应第i个限位装置的质量；kTAi对应第i根杆的刚度数值；L对应的是锚段的整体长度；p、w各自对应一定区域中吊弦、杆的全部数目。网模型和弓模型通过接触力进行耦合。

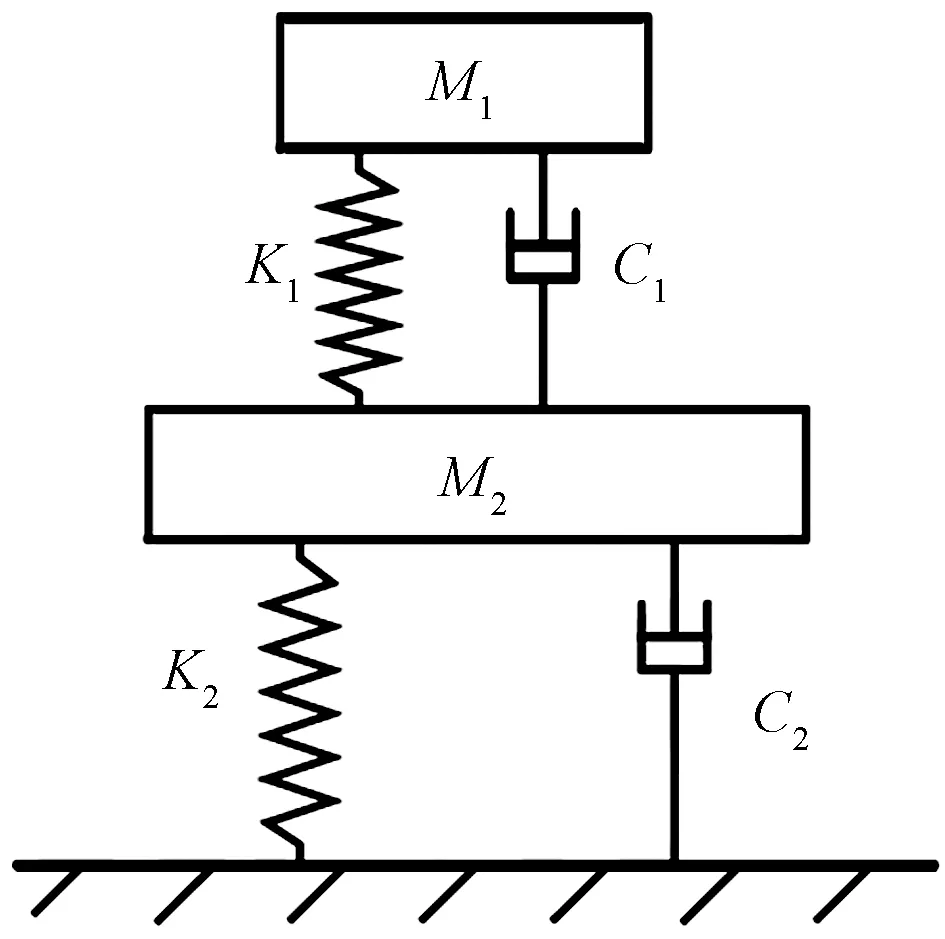
图2 受电弓二元集中质量简化模型Fig.2 Simplified model of pantograph bivariate lumped mass

图3 弓网耦合系统模型Fig.3 Pantograph-catenary coupling system model

接触线和承力索的位移可以表示为

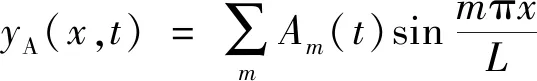
(1)

(2)

式中：Am对应相关线路的第m项数值；Bm对应连接线路的第m项数值；x代表X轴向坐标；L对应一个区间的整体长度。采用拉格朗日方法推导弓网耦合系统的运动方程，即

(3)

式(3)中：y1为受电弓弓头位移；y2为框架位移，吊弦刚度表示接触线与吊弦连接处的力。弓网耦合系统基本参数如表1所示。

采用Newmark法对运动方程(3)进行求解，最终得到了列车在360 km/h速率下的弓网接触力时域曲线，如图4所示。

在一个区间中，连接压力在一定坐标中与吊弦等位置形成明显的变化。在支柱部位上，连接压力实现了峰值，这考虑跟定位器以及吊弦位置的质量高度集中相关，在这种情况下会使得惯性力不断变大。

根据弓网接触力时域曲线，最终得到受电弓对车厢产生的激励力频域特性曲线，如图5所示。

图4 360 km/h速率下弓网接触力时域曲线Fig.4 Time-domain curve of pantograph-catenary contact force at 360 km/h rate

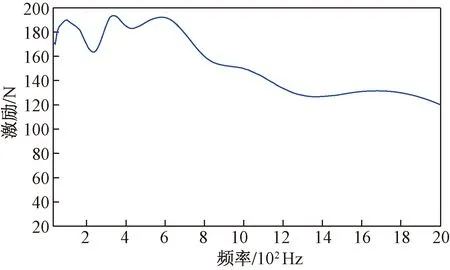
图5 360 km/h速率下受电弓对车顶激励的幅频特性曲线Fig.5 Amplitude-frequency characteristic curve of pantograph excitation to roof at 360 km/h rate

2 沟槽橡胶复合隔振结构

对于受电弓形成的振动，通过复合隔振结构降低受电弓传递到车厢结构的能量。复合隔振结构重点通过5层结构形成，从上部到下部，最上层是橡胶沟槽，最下层为橡胶沟，上沟槽的拓展方位和下沟槽的延伸方向互相垂直。结构隔离层的材料为木屑。沟槽橡胶复合隔振结构的组成如图 6所示。

图6 沟槽橡胶复合隔振结构组成Fig.6 Composition of groove rubber composite vibration isolation structure

采用有限元软件ANSYS预测沟槽橡胶复合隔振结构的动力学隔振效果。在创建相应的研究模型时，先需要创建相符合的不同位置的金属基座，在上部位置中施加了30～2 000 Hz的作用力，具体的方位与大平面的区位保持一致。边界条件为上下基座短边固定。材料属性如表2所示，具体的有限元二维模型如图7所示。

表1 弓网耦合系统基本参数Table 1 Basic parameters of pantograph-catenary coupling system

通过隔振结构下基座位置的加速度级为分析隔振性能的关键指标。在下部位置的相同平面中设定了较多的点，同时对不同的点完成加速度级的能量平均，从而形成了相应的等效加速度级。此时运用到的分析公式为

(4)

(5)

式中：以a0为基准加速度，10-6m/s2。在下基座选取4个点作为加速度输出点以计算等效振动加速度。

表2 材料属性Table 2 Material properties

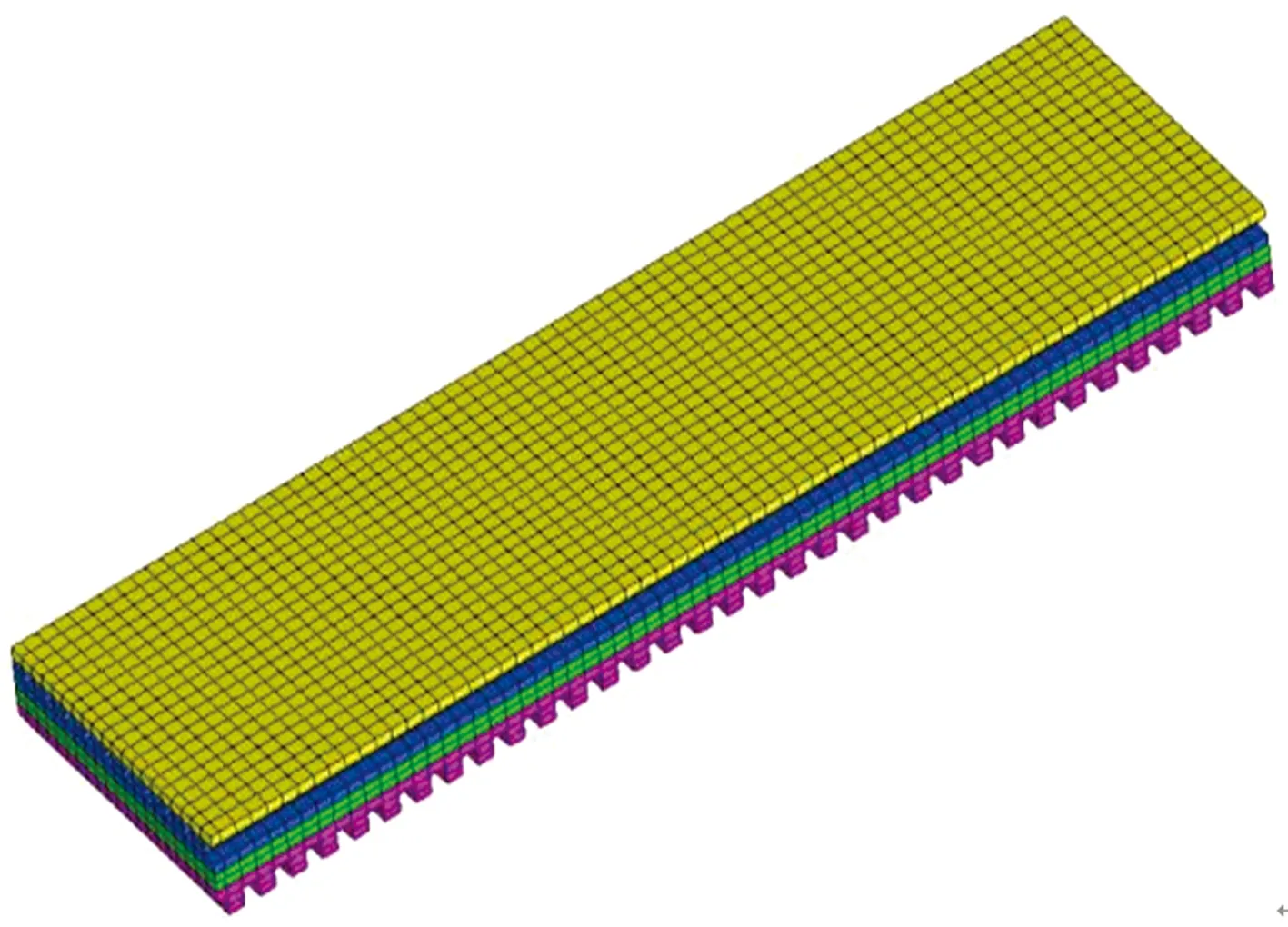
图7 复合隔振结构有限元模型Fig.7 Finite element model of composite vibration isolation structure

为进一步测试复合隔振结构与其他类似隔振结构相比存在一定的优势，将沟槽橡胶复合隔振结构与纯橡胶材料及无沟槽隔振结构的隔振效果进行对比。沟槽橡胶复合隔振结构尺寸参数如表3所示。

纯橡胶形式与隔振结构，在规格上与沟槽方案基本保持一致。另外不同座的边界因素也维持吻合，输出位置保持的位置是相同的。无沟槽橡胶隔振结构中间也带有隔离层。沟槽复合隔振结构及无沟槽隔振结构与纯橡胶隔振结构对比如图8、图9所示，在30～1 300 Hz的频率区间中，带沟槽结构的实际隔振效果显然超过纯橡胶材料及无沟槽隔振结构的隔振效果，在忽略高频振动的情况下，带沟槽结构体现出相应的优势。由于受电弓对车厢的冲击在低频范围相对较大(图5)，因此针对受电弓冲击，带沟槽的复合橡胶隔振结构具有更好的隔振效果。

表3 沟槽橡胶复合隔振结构尺寸Table 3 Dimensions of rubber composite vibration isolation structure with grooves

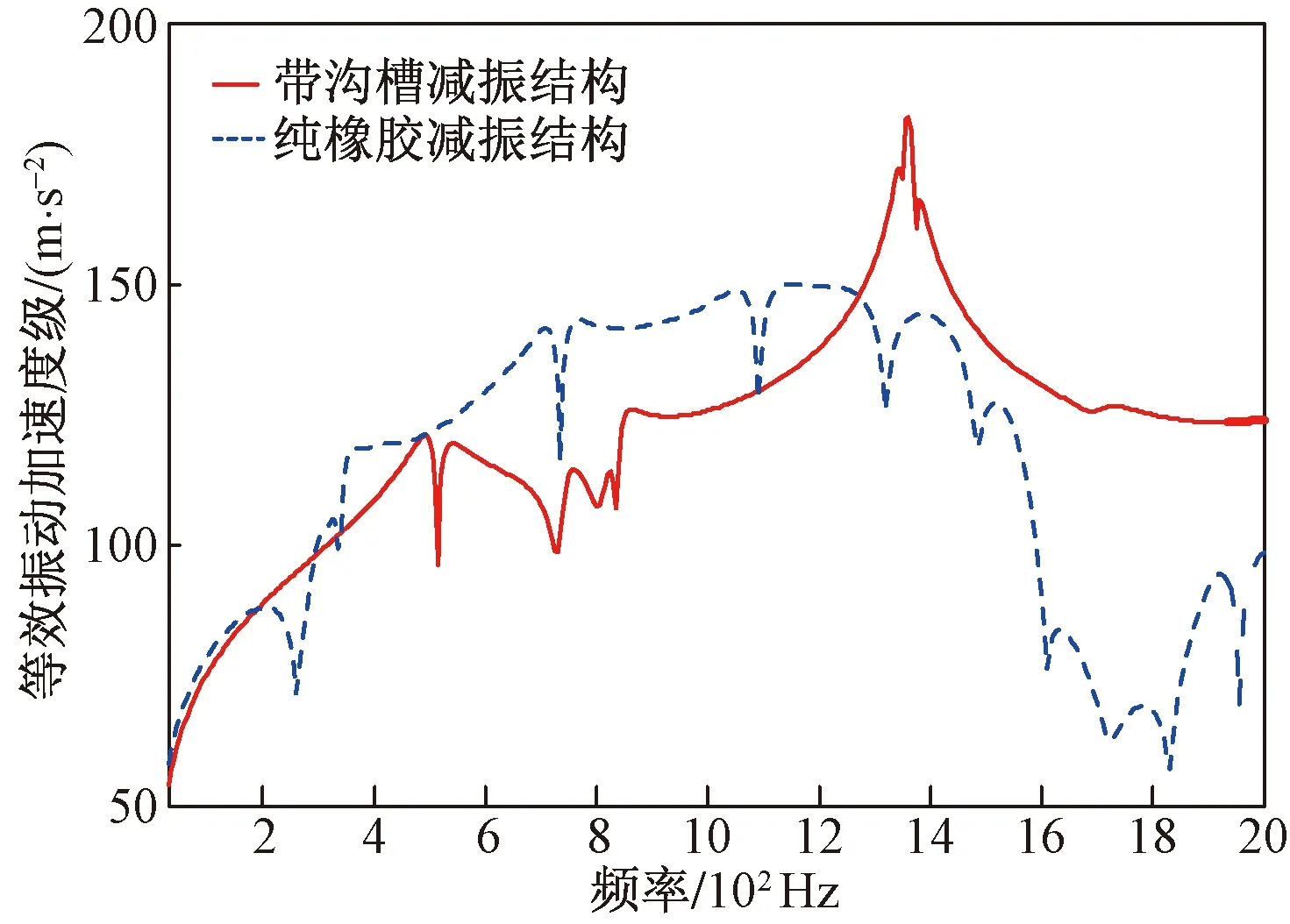
图8 沟槽橡胶复合隔振结构与纯橡胶结构隔振对比Fig.8 Comparison of vibration isolation between grooved rubber composite isolation structure and pure rubber structure

图9 沟槽橡胶复合隔振与无沟槽隔振结构的隔振对比Fig.9 Vibration isolation contrast of grooved rubber composite vibration isolation structure and grooveless vibration isolation structure

3 基于沟槽橡胶复合隔振结构的车厢内部降噪分析

为验证沟槽橡胶复合隔振结构的隔振降噪效果，将该隔振结构应用于受电弓和车厢的连接位置，和无隔振的车厢振动情况进行对比，借助声学模拟软件 Virtual. Lab 分析车厢中存在隔振和无隔振，两种不同情形下的具体声场状态[20]，研究是否具有隔振结构后所具备的实际降噪效果。

3.1 车厢振动响应分析

建模时，车体主要部分结构的截面如图 10所示。主要采用四节点等参壳单元来建立车厢结构的有限元模型。壳单元厚度为3 mm，并根据图 10在对应位置加筋以增加车体刚度。

在进行声腔模型的建模时，在车厢结构有限元模型的前提下，借助车厢结构的内表层，从而创建内部环境的声腔模型。其具体运用的是六面体网格的形式，同时设定FLUID30三维流体的单元特征。在运算过程中，设定声音在空气中的传播速度为 340 m/s，空气的密度为1.29 kg/m3。

在添加了隔振方案后，外部激励作用的幅频保持固定，此时的外部位置设定即为受电弓的垂直方位，具体如图11所示，此时全部车厢结构的振动作用分析对比如图12所示。在加载了隔振结构之后，车厢结构的振动响应几乎在全频段内明显降低。

图10 车厢几何模型及各部分结构Fig.10 Geometric model of carriage and structure of each part

图11 受电弓安装点激励加载示意Fig.11 Illustration of pantograph installation point excitation loading

图12 典型点的振动加速度对比Fig.12 Vibration acceleration comparison at typical points

3.2 加载隔振结构的车厢内部降噪分析

将计算完成的车厢外层加速度设定成条件因素，从而输入专业分析软件中，利用边界元法完成分析和推理过程。此次研究中，对车厢整体一共选择6个测试的位置。下部位置点视为原点，此时车厢的全部长度设定成x轴，宽对应为y轴，高对应为z轴，那么此时选定的6个检测位置，举例说明A(0，0，1.2)，F(-8，0，1.6)，具体的点的位置如图 13所示。

图13 车厢内部测量点位置分布Fig.13 Distribution of measuring points in carriage

装有隔振结构及无隔振结构情况下，车厢6个测点的声压曲线对比如图14所示，这里的蓝色线条对应为无隔振状态下的声压级，红色虚线对应为添加了隔振后的声压级。在发挥了隔振结构的效果后，内部环境中全部频段区间中的降噪效果都实现了大幅度的下降。声压级基本能够减少到 20 dB 左右。不同频率状态下，其声压级减小的幅度存在不同，这考虑跟隔振结构在不同频率下实现的隔振效果具有差异相关。因为隔振结构对车厢门内部环境中的动态特征同样具有相应的作用，因此在声压的分布特征上同样带来了改变效果，声压的浮动变化呈现为不稳定性，在分布趋势的变化上形成了两个低谷。综合来看，沟槽橡胶复合隔振结构能够有效降低受电弓引起的噪声。

4 结论

以列车车厢为研究对象，研究沟槽橡胶隔振结构对车厢噪声的降噪效果。对弓网耦合系统进行了分析研究，相应地推测了弓网耦合体系的微分方程组，同时结合Newmark 数值积分方式，运算得到了受电弓对上部位置激励作用形成的幅频特征。根据运算结果观察到，受电弓对车厢的激励幅值随着频率的增加逐渐降低，低频激励力幅值接近200 N，高频激励力幅值在100 N以上。

借助有限元方法研究了复合隔振结构的频谱规律，同时和纯橡胶模式、无沟槽隔振模式等具备的隔振效果进行具体的比较研究，从而论证了复合结构在频段较低的区间中，体现出更低的加速度响应。以本文所预测的受电弓激励力为输入，利用有限元方法分析了车厢在安装及不安装沟槽橡胶复合隔振结构情况下的动力学响应。分析表明，沟槽橡胶复合隔振结构在全分析频段内能够有效降低车厢结构的振动量级。利用直接边界元法进行了车厢内部声场分析，结果显示沟槽橡胶复合隔振结构能够将车厢内的噪声平均降低约20 dB，具有明显的降噪效果。

图14 声压级对比Fig.14 Sound pressure level comparison chart