山岭隧道洞口段衬砌结构地震响应数值分析

何则干, 王小威, 左正波

(1.广州市市政工程设计研究总院,广州 510060；2.长江勘测规划设计研究有限责任公司,武汉 430072；3.武汉大学水利水电学院,武汉 430072)

山岭隧道是中国交通运输的重要部分,其对中国的经济建设起到了不可替代的作用。由于中国是一个地震多发国家,不少重要的山岭隧道位于中国地震多发区。近年来的强震灾害调查发现[1-3],隧道洞口段和地质环境急剧变化的洞身段是山岭隧道震损最严重的部位。因此,研究山岭隧道洞口段结构地震响应对于保障其在地震过程中的安全稳定具有较大意义。

通常认为,隧道洞口段是仅次于断层破碎带影响区域的抗震薄弱部位[4-6],其抗震稳定性差的主要原因是洞口覆盖层较薄,并且多为严重风化的堆积体,其在外荷载扰动下容易造成山体失稳以及洞口垮塌[7-8]。另外,洞口边坡自由面对地震波有放大作用,进一步加大了地震荷载对洞口结构稳定性的不利影响[9]。目前,中外学者采用各种方法分析洞口段隧道地震响应特征。Shen等[10]调查了汶川地震中52座隧道的震损情况发现,在震损的30座隧道中有13座隧道洞口段发生了严重震损的情况。王峥峥等[11]统计了对汶川地震四川灾区中的56座隧道的震损情况,并总结出了影响隧道洞口震害的主要因素。Yashiro等[12]统计了2004年Niigataken-Chuets地震中隧道结构的震损情况,总结了洞口段结构震损机制。Tao等[6]采用振动台模型试验分析了山岭隧道洞口段结构横向和纵向变形特征,分析结果显示隧道两侧拱肩与拱脚为抗震的薄弱环节。申玉生等[7]以雅泸高速公路某隧道为原型,利用大型振动台研究了山岭隧道洞口段结构动力响应特征,研究指出减震层能有效地减小地震对洞口结构的破坏。蒋树屏等[13]对嘎隆拉隧道洞口段展开了振动台模型试验研究,分析了洞口结构的加速度和应变响应特征,结果显示峰值加速度沿边坡坡脚至坡顶不断增大。许江波等[14]对罗沙隧道进行了高地应力下硬岩隧道洞口爆破开挖振动监测试验,对振动数据进行了归一化处理,得到了关于硬岩隧道洞口爆破振动的规律,为爆破开挖设计优化提供了参考价值,对洞口段动力响应研究有一定的参考价值。Wang等[9]分析了围岩与结构动接触和动水压力对水工隧洞洞口段结构地震响应的影响,并分析了洞口段结构的损伤机制。高峰等[8]采用隐式动力有限元方法分析了不同围岩材料和衬砌类型条件下,隧道洞口段衬砌的应力和位移规律。张伟等[15]采用有限元方法分析了滑坡对隧道洞口稳定性的影响,并提出了相应的加固措施。以上研究有效地提升了中国隧道抗震设计水平,但是目前对于隧道洞口段结构在地震过程中的动力响应规律以及破坏机理的认识仍不够深入,需要进一步研究。

鉴于数值方法在进行隧道洞口段结构这类复杂非线性系统动力分析时的高效性,采用三维非线性有限元模型模拟了山岭隧道洞口段结构的地震响应过程,分析了洞口结构横截面和纵向响应特征,以便为山岭隧道洞口段结构的抗震设计提供参考。

1 理论基础

1.1 混凝土损伤塑性本构模型

混凝土是一种非均质预先有微裂缝的材料,地震作用下易产生损伤,表现为材料性质的劣化,可以用损伤因子来描述混凝土的这种损伤机制。在单轴单调受拉或受压条件下,考虑损伤后的混凝土应力-应变关系为

(1)

试验表明，单轴循环荷载作用下，当荷载方向变化时，混凝土的部分弹性刚度会恢复，为此引入损伤因子d来描述这一效应。单轴循环荷载下损伤因子d为应力状态、dt、dc的函数：

1-d=(1-stdc)(1-scdt)

(2)

式(2)中：st、sc为与应力状态有关的函数，0≤st,sc≤1，分别表示为

(3)

式(3)中:ωt、ωc为刚度恢复权重因子，与材料性质有关，用来描述反向荷载下材料的刚度恢复程度。

(4)

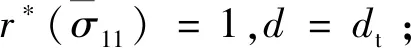
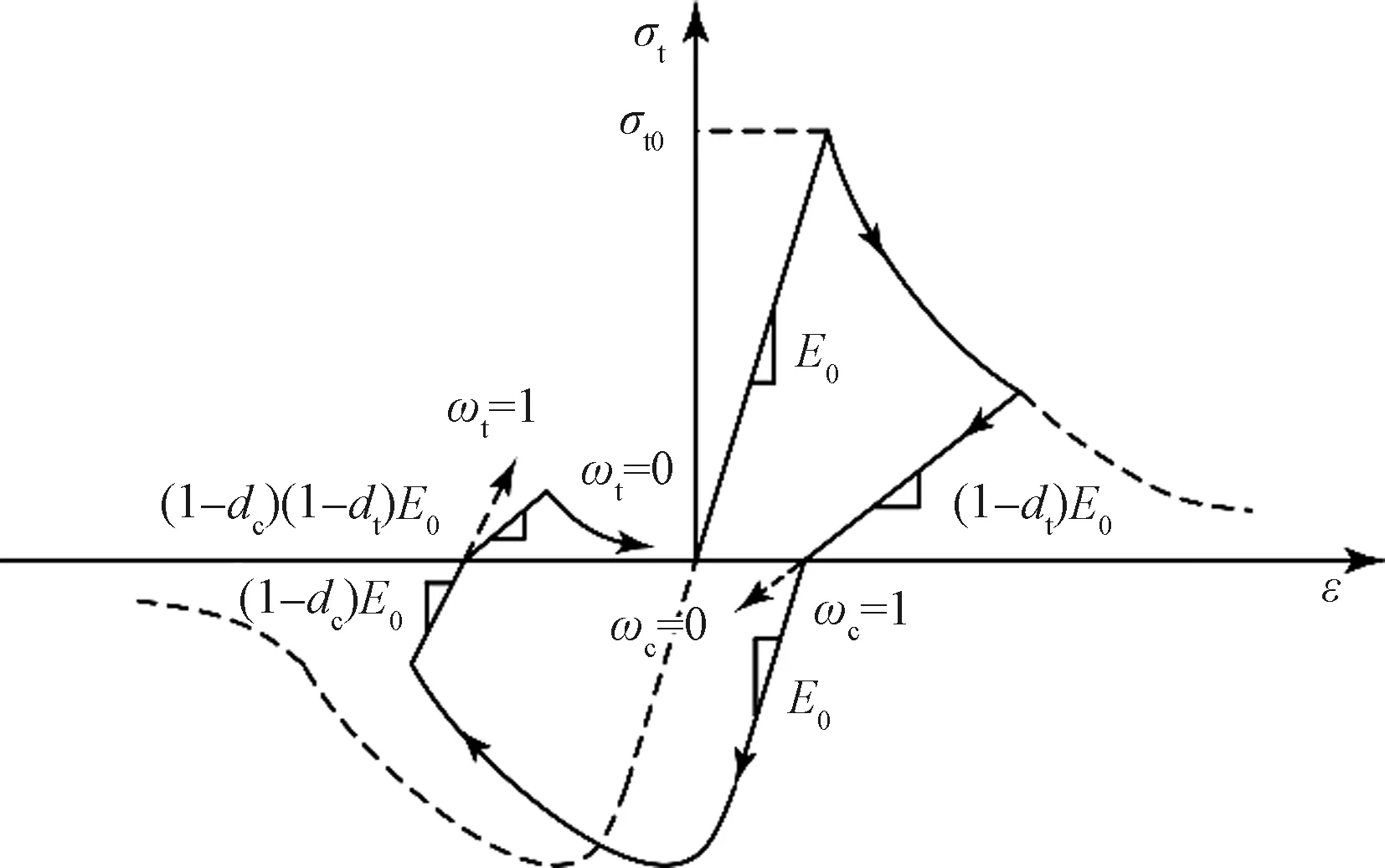
图1 单轴循环荷载下混凝土应力-应变关系Fig.1 Stress-strain relationship of concrete under uniaxial cyclic load

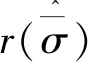
(5)

(6)

三维应力条件下混凝土的损伤塑性应力-应变关系以张量形式表示为

(7)

1.2 三维地震波场求解方法

系统的运动微分方程为

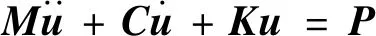
(8)

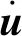
采用显示中心差分法求解式(8)，根据中心差分法，系统内节点的时域逐步积分格式为

(9)

(10)

(11)

式中:I为单位阵；Δt为积分时步。

满足式(9)～式(11)求解格式稳定性的条件为

(12)

式(12)中:Ω=ω0Δt，ω0为系统结构自振圆频率；ζ为系统结构阻尼比[16-18]。

为考虑动力响应的计算效率，在满足稳定性条件式(12)的前提下时步尽可能大，时步约束条件为

(13)

式(13)中：ωmax为系统最大振动频率。

me=∭ρNTNdxdydz

(14)

(15)

式中:N为形函数矩阵；ρ为系统内单元密度;ne为系统单元总数。

阻尼反映了材料减震耗能能力[19],采用瑞利阻尼模拟阻尼效应临界阻尼系数,取0.05。

2 数值模拟分析

2.1 工程概况

横琴新区长湾隧道工程位于珠海市横琴新区，工程北起富祥湾路，南抵环岛南路。工程总长约1.6 km，拟采用双向6车道规模，包含山岭隧道、两侧连接线道路及设备北侧设备管理用房。其中山岭隧道穿越大横琴山，近南北走向，由东、西两支组成：东线隧道起点里程EK0+220.0，止点里程EK1+265.0，长1 045.0 m；西线隧道起点里程WK0+230，止点里程WK1+220.0，长990.0 m。如图2所示，北端、南端均采用削竹式洞门。

图2 长湾隧道洞口段Fig. 2 Portal sections of Changwan tunnel

拟建隧道范围内基岩为花岗岩，表部强风化层较薄，自然山坡稳定，无崩塌、滑坡、泥石流等不良地质现象，洞口岩体较稳定，适宜洞口建造(图3)。场区属丘陵地貌，丘岗周边为冲洪积平原，同时未见具明显活动性的断裂构造，判断该隧道区的地应力为静应力，无构造应力作用。设计采用三车道标准断面基本形式，隧道拱部采用三心圆，侧墙为大半径圆弧，仰拱与侧墙之间用小半径圆弧连接。

图3 长湾隧道洞口地貌Fig.3 Landform of Changwan tunnel portal

2.2 计算模型与参数

选取东线隧道 EK0+220.0～EK0+620.0段进行洞口段的地震响应分析。隧道最大埋深115 m，洞口边坡坡角约22°，最大开挖尺寸15.48 m×10.2 m(宽×高)。混凝土衬砌采用C30，厚0.6 m；仰拱回填材料采用C20混凝土。

建立该段的三维有限元模型，全部采用八节点六面体单元进行离散，共剖分99 920个单元和105 473个节点，其中衬砌单元12 000个。模型x轴沿水平向与洞轴线垂直，y轴沿洞轴线方向，z轴与大地坐标一致。有限元模型的具体尺寸如图4所示，隧道横断面如图5所示。材料力学参数取值如表1所示。

图4 洞口段有限元模型Fig.4 Finite element model of portal section

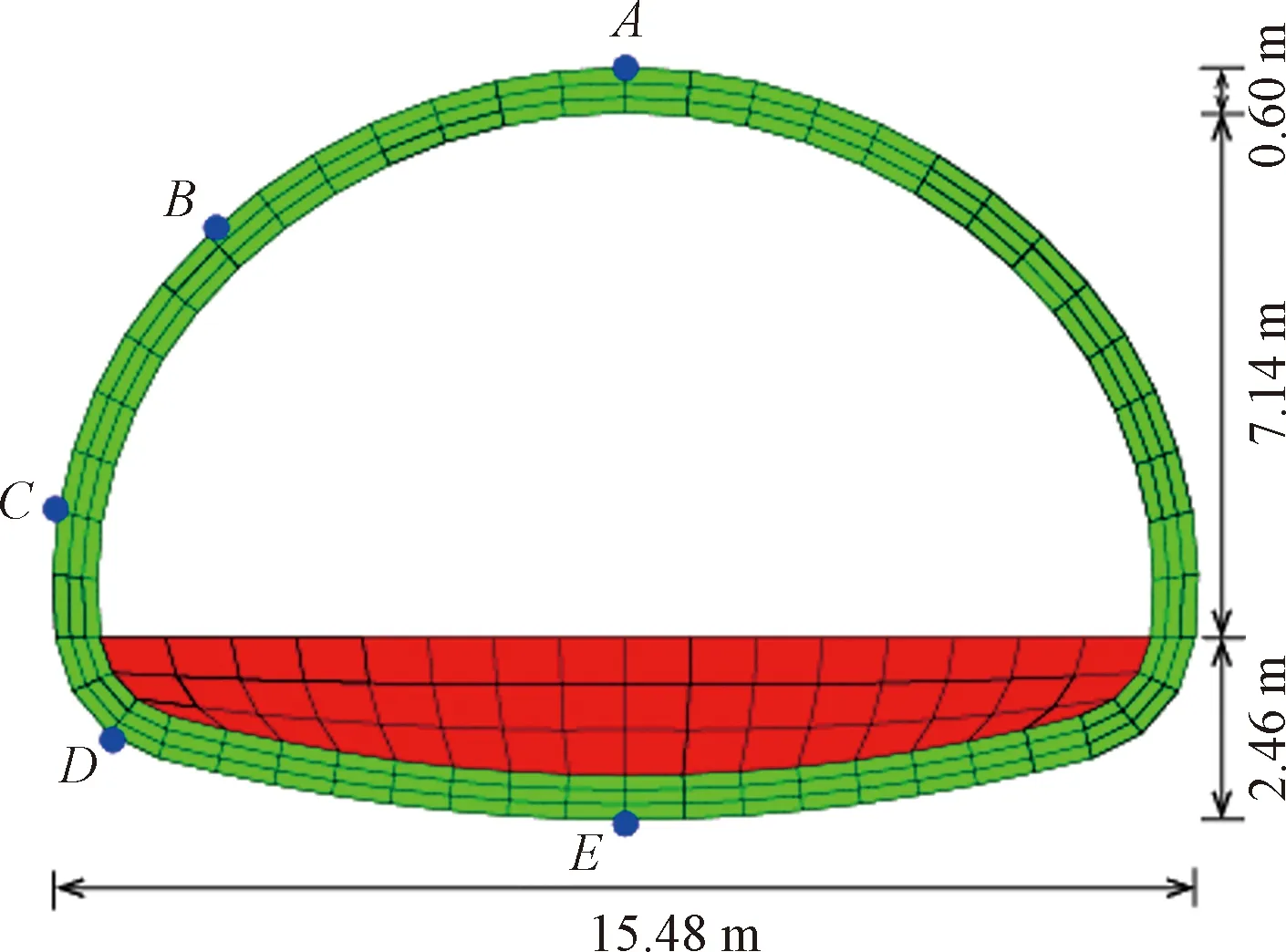
图5 隧道横断面图Fig.5 Cross section of tunnel

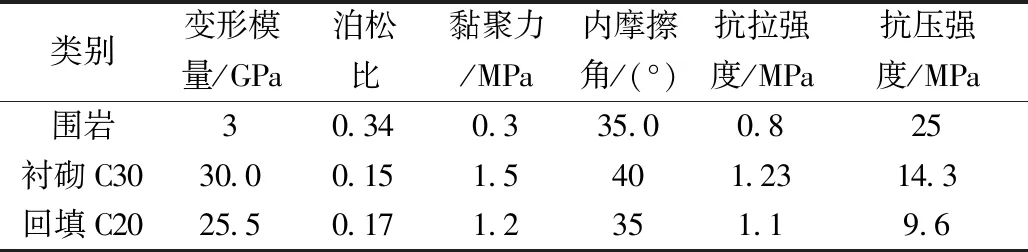
表1 材料力学参数Table 1 Mechanical parameters of materials

2.3 计算条件

根据《广东省地震烈度区划图》，场区的地震基本烈度为VII度，据《建筑抗震设计规范》(GB 50011—2001)场区的抗震设防烈度为7度，设计基本地震加速度为0.10g。场地土的类型为软弱土-中硬土，大部分地段等效剪切波速(Vse)一般满足条件：250 m/s≥Vse>150 m/s，场地覆盖土厚度一般大于3 m，小于50 m，根据《建筑抗震设计规范》(GB 50011—2010)，隧洞所在位置为Ⅱ类建筑场地，特征周期为0.35 s。

根据上述场地地震特性，绘制了场区的设计加速度反应谱，并根据反应谱人工拟合了1条地震波作为x向输入波，如图6所示。地震作用同时考虑x向和z向激励，z向输入波加速度时程取为x向的2/3。计算过程中，岩石材料采用带拉伸截止限的Mohr-Coulomb模型模拟，混凝土材料采用第2章介绍的本构模型模拟，计算平台采用自主开发的三维动力有限元计算程序[20]。模型四周采用自由场人工边界，底部采用黏弹性人工边界，地震波从模型底部输入。另外，需要注意的是，由于现场缺乏实测地应力，在开挖计算时采用自重应力场作为初始地应力场，并将开挖计算获得的应力场作为动力计算的初始条件。

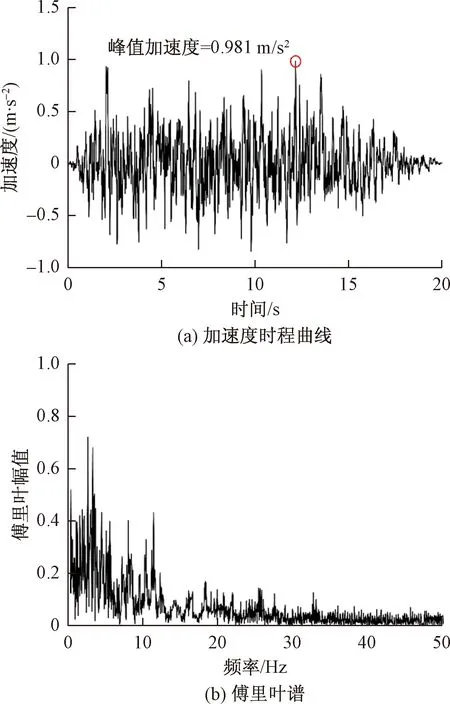
图6 x向输入波加速度时程和傅里叶谱Fig. 6 Acceleration time-history and Fourier amplitude of x directional input wave

2.4 计算结果分析

为研究浅埋段衬砌结构的地震响应特性，沿隧道轴线每隔40 m建立1个监测断面，共计10个监测断面。在每个监测断面上布置了5个监测点(图5)，图5中A、B、C、D、E分别对应衬砌顶拱、拱肩、拱腰、拱脚和仰拱，以监测对应部位的应力、位移等时程特性。

2.4.1 衬砌位移分析

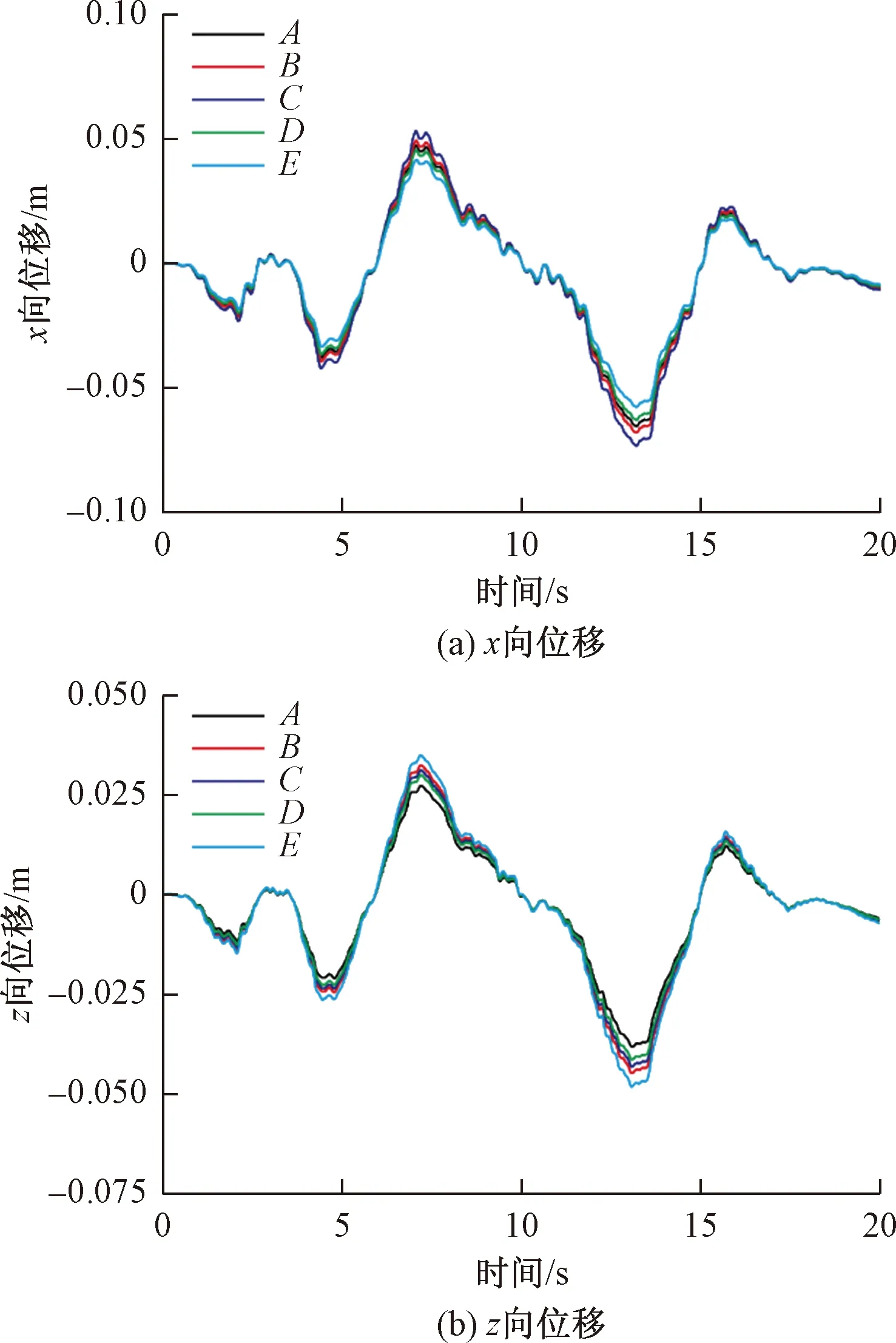
图7 衬砌监测点位移时程Fig.7 Displacement time-histories of monitoring points of lining

图7展示了地震过程中洞口监测断面上监测点的水平横向(x向)和竖直向(z向)位移波动情况。可以看出，各监测点位移波动规律基本相似，在t=7.5 s和t=13 s左右均经历了一个较大的波峰和波谷，说明衬砌结构各部位在地震过程中是处于同步振动的状态。由图7(a)可以看出，各个监测点水平横向位移波动规律的主要差别在于位移幅值，拱腰和拱肩的水平横向位移幅值明显大于其他部位的位移幅值，最大位移值出现在拱腰，其值为7.3 cm。由图7(b)可以看出，各点竖直向位移曲线的主要差别也是在于位移幅值，最大竖直位移值出现在仰拱部位，其值为4.8 cm。另外，衬砌各部位位移值有较为明显的差别，说明衬砌结构在地震过程中发生了明显的结构变形。一旦这种结构变形超过了其强度阈值，则很可能发生结构破坏。

图8展示了衬砌10个监测断面各监测点位移峰值沿洞轴线方向变化规律。可以看出，衬砌各个部位x向位移峰值随着其距洞口距离的增加而不断减小，说明距离洞口越近，结构的位移响应越大。另外，随着距洞口距离的增加，位移幅值下降的速度越来越小。此外，距离洞口越近，衬砌各部位的相对位移就越大，衬砌结构变形也越大。这主要是由于当距离洞口较近时，洞口边坡自由面反射地震波与入射地震波形成复杂的地震波场，并对隧道结构产生较大影响；而当距离洞口较远时，反射地震波的影响则较小[6]。同理，衬砌各个部位x向位移峰值沿洞轴向的变化规律与x向相似。

图8 衬砌监测点峰值位移沿洞轴线的变化Fig.8 Peak displacement of monitoring points of lining along tunnel axis

2.4.2 衬砌应力分析

衬砌结构洞口监测断面各监测点最大和最小主应力时程如图9所示。由图9(a)可知，各个监测点t=0～2.5 s时间段内应力水平较小；在t=2.5～17.5 s时间段内最大主应力波动剧烈，说明衬砌结构在此段时间内经历了强烈的循环加卸载过程。另外，各个监测点最大主应力峰值均表现出拉应力状态，其中拱肩(B点)和拱腰(C点)部位的最大主应力峰值明显大于其他部位，说明这些部位在地震过程中遭受了较大的拉应力。还需要注意的是，拱肩、拱腰和拱脚(D点)部位的最大主应力峰值明显超过了混凝土的抗拉强度1.23 MPa，说明这些部位易发生拉裂损伤。由图9(b)可知，衬砌各部位最小主应力应力水平较小，最小主应力峰值均没有超过混凝土抗压强度。综合图9可以看出，受拉破坏是洞口衬砌主要的破坏模式，在进行隧道洞口衬砌结构设计时，需要注重衬砌结构的限裂设计。

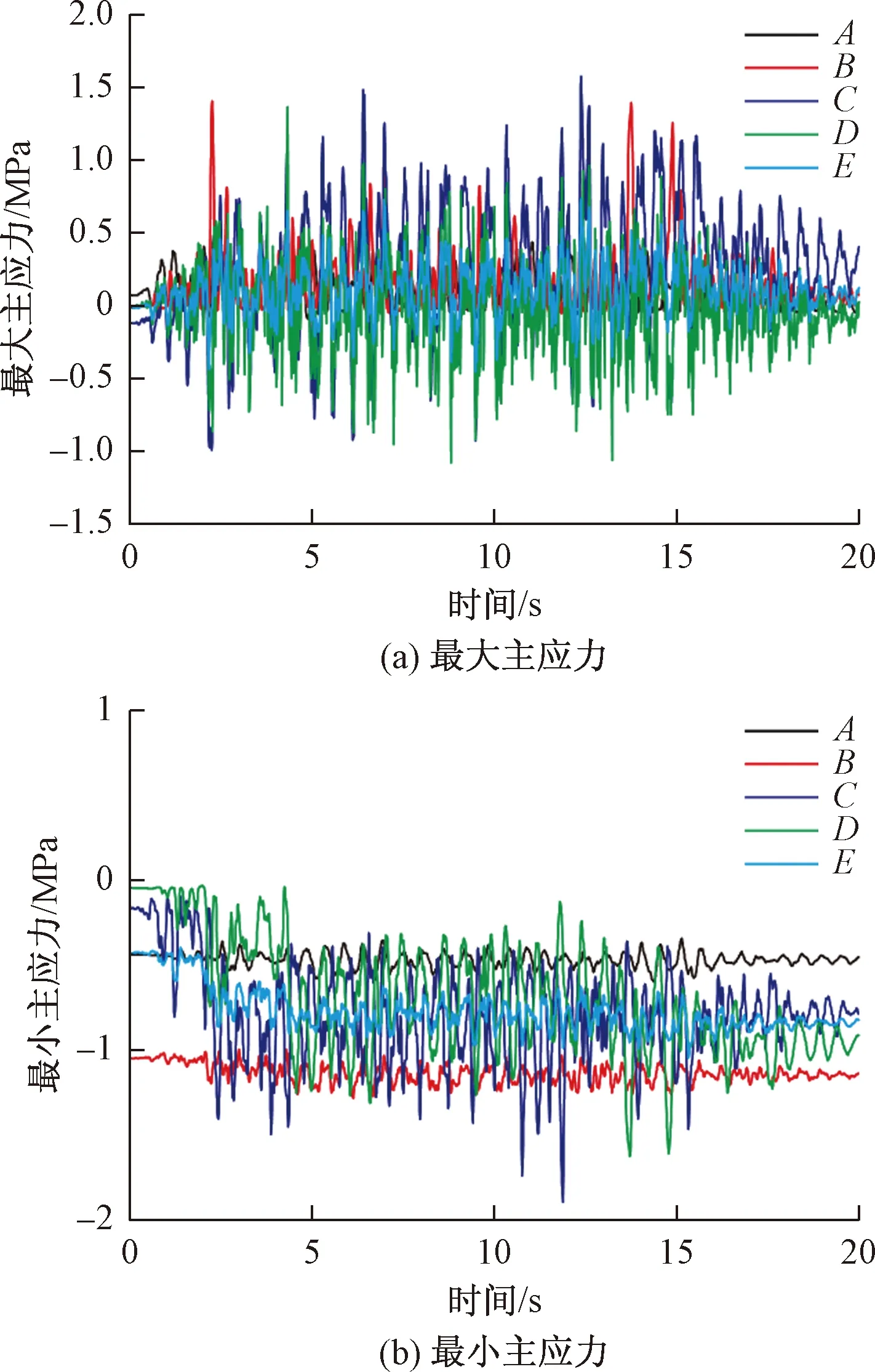
图9 衬砌监测点应力时程Fig.9 Stress time-histories of monitoring points of lining

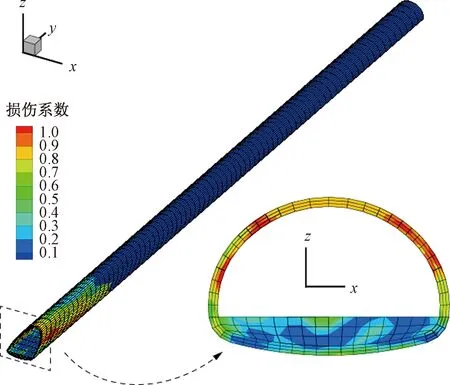
图10 震后衬砌损伤系数分布Fig.10 Damage coefficient distribution of lining after earthquake

2.4.3 衬砌损伤分析

图10为地震后隧道衬砌结构损伤系数分布。由图10可以看出，衬砌结构不同部位损伤程度不同。从隧道纵轴向看，损伤区域主要分布在距离洞口70 m范围内的衬砌结构上，而且距离洞口越近，损伤系数越大，该结果也与前面分析的衬砌结构位移和应力响应结果相吻合；从隧道横向看，衬砌拱肩和拱腰部位的损伤系数明显大于其他部位，其损伤系数d最大值接近1，说明隧道衬砌拱腰和拱肩是其抗震的薄弱部位，需要强化这些部位的抗震设计。另外，若定义损伤系数d大于0.7的区域为严重损伤区域，则严重震损区主要分布在距离洞口60 m范围内。

3 结论

基于建立的可考虑混凝土结构损伤状态的非线性有限元模型，分析了某隧道洞口段衬砌结构的地震响应过程，分析得出如下结论。

(1)衬砌结构各部位在地震过程中是处于同步振动的状态，各部位水平横向位移的主要差别在于位移幅值，其中拱腰和拱肩的水平横向位移幅值明显大于其他部位的位移幅值。

(2)衬砌结构的位移响应和各部位的相对位移随着距离洞口的距离的减小而不断增大，说明距离洞口越近，衬砌结构变形越大。

(3)拱肩和拱腰的最大主应力峰值明显大于其他部位，并且拱肩、拱腰和拱脚的最大主应力峰超过了混凝土抗拉强度，说明受拉破坏是洞口衬砌主要的破坏模式。

(4)衬砌结构的损伤区主要分布在距离洞口70 m范围内的衬砌结构上，而且距离洞口越近，损伤系数越大；衬砌拱肩和拱腰部位的损伤系数明显大于其他部位，说明隧道衬砌拱腰和拱肩是其抗震的薄弱部位。