公路机电工程最优投标报价仿真研究

姜绵峰，叶春明

(1.中远海运科技股份有限公司，上海 200135；2.上海理工大学 管理学院，上海 200090)

0 引 言

近期，国家发展改革委、中央网信办和科技部等11个国家部委联合印发了《智能汽车创新发展战略》，随后国家重点研发计划项目“高速公路智能车路协同系统集成应用”获批立项，与之相关的车路协同、路侧智能设施、云控平台和自动驾驶等技术得到广泛关注，智能交通行业的发展机遇与发展风险骤增。在此背景下,高速公路机电工程从业单位需从资金和技术储备方面做好应对准备，保证现金流和利润稳定，提高相关项目投标的中标率。

国有资金投资的公路工程主要采用公开招投标的方式确定承包合同金额，即中标金额。在招投标阶段，重点从委派人员资历、类似工程业绩、信用评价等级和投标报价金额等方面评选中标单位。在行业技术水平同质化的背景下，投标报价逐渐成为从业单位竞争中标的关键指标。国外学者对此开展了一系列研究，例如：OO等[1]研究了竞争程度对投标决策的影响；HOSNY等[2]研究了不同评价策略下最优利润的综合模型；AZIZ等[3]研究了不平衡报价中利润与报价的最优平衡;CHAO等[4-5]采用因素回归分析方法测算了最稳妥的成本利润率和不同成本利润率的报价中标率。

在工程成本和报价中标方面：彭梅等[6]运用成本空间和性能因素研究了最优竞标价；刘康等[7]分析了成本函数和报价指数分布的最优报价区间；龚玉云等[8]采用风险效用函数研究了成本复合标底的最优报价模型；丁天维等[9]对比研究了计划评审法和复合标底法中利润与中标收益的变化关系；李建光等[10]采用单纯形法测算了工程量清单预算单价的最优值；李登峰等[11]研究了对称报价策略中既定风险系数和成本系数的报价迭代优化，结果表明,竞争单位工程成本估计误差较大，同时评标办法未考虑实际工程成本。

在最优投标报价方面：雷文华等[12]利用概率论解析了合成标底的最优报价函数；陈起俊等[13]对3类风险情况下的最优报价进行了预测；黄敏等[14]借助博弈论和扣分矩阵确定了满分报价区间；黄朝煊等[15]和李莹[16]采用随机概率研究了业主期望标底和权重系数随机变化中的最优报价计算。

国内研究的投标报价均值都为简单算术平均值，而当前的评标已逐渐采用二次算术平均值计算评标基准价。对此，本文建立二次均值法的基准价解析式，并在样本概率分布的基础上模拟测算最优报价水平。

1 投标博弈模型

1.1 假设和模型参数

基本假设：

1)开标之前投标人之间的报价信息相互保密，不可知；

2)各投标人采取的评标办法相同，中标的不确定性对称；

3)投标人的收益只与报价有关，投标成本忽略不计；

4)投标人的风险偏好都呈中性，目标追求收益最大化。

定义招标控制价为A，有效投标个数为n(n≥3),第i个投标报价为vi，己方报价为R，竞争对手投标报价平均值为Z，评标基准价为S，招标控制价的权重系数为β，平均报价下浮率为α，投标报价的扣分函数为L。

1.2 最优报价模型

投标人之间博弈的行动没有先后顺序，且其他人的信息不完全掌握，属于非完全信息静态博弈的情况。根据上述假设，投标博弈的参与者即为各独立的投标人；博弈的策略集为各投标人执行本单位的最低施工预算，争取最大的中标概率；博弈的支付函数为投标报价中的相对利润，其比例由各投标人自己确定。根据评标办法得出的最优投标报价即为博弈结果。首先，统计总体平均报价与招标控制价组合而成的评标基准价；然后，根据评标基准价和扣分规则计算投标报价的评标得分，得分最高者(即扣分最少的报价)即为最优投标报价。具体的计算过程为

(1)

S=[β·A+(1-β)·K](1-α)

(2)

(3)

L→min,R→max

(4)

一般情况下，招标文件中的投标人须知和评标办法项目会注明招标控制价A、扣分函数L和权重系数β。在开标现场，对应的平均报价下浮率α、投标人总数n和竞争对手投标报价平均值Z决定得分最高的投标价。根据式(4)进行优化求解，可得出满分的报价值R为

(5)

2 蒙特卡洛仿真

2.1 评标基准价

当不考虑报价以外的影响因素时，采用常见的合理低价法和综合评分法无法解决围标异常问题，即多数投标报价集中迫使平均报价接近或等于某个报价水平，造成投标人数较多的报价区间的评标得分比投标人数较少的报价区间的评标得分更高，没有竞争效果。因此，很多招标单位在计算报价得分时逐渐采用二次平均的方法计算基准价，即将所有投标报价按从高到底的顺序排序之后，划分为不同区段，由各区段的报价均值计算出评标基准价，这样能避免多数投标报价的权重过大引起评标价被控制。图1为二次平均报价计算。二次均值基准价K′的计算过程如下。

图1 二次平均报价计算

1)收集参与评标的全部有效报价，确定投标人数、最大报价和最小报价。由式(6)和式(7)可计算得到二次均值的分段数量和间隔区间；由式(8)和式(9)可计算得到不同分段的边界值。

(6)

(7)

(8)

(9)

2)根据报价各分段区间的边界值统计隶属于不同分段的报价综合和个数。由式(10)计算各分段的平均报价值。

(10)

3)根据各分段的平均报价值，由式(11)计算二次平均报价K′，用K′替换K代入式(2)，可计算出新的评标基准价S′，代入式(3)计算各报价的扣分值，根据评标得分值对各组报价进行排序，即可得出中标报价。

K′=average(Kη)，η=1，…，θ

(11)

2.2 仿真报价分析

由上述计算和统计学原理可知，投标人数、招标控制价、报价极大值、报价极小值、报价金额统计分布和下浮率是决定二次算术平均的重要指标。当前大部分研究都假设报价数值满足均匀分布，但金琦[17]、吕炜等[18]和蒲勇[19]的研究表明，报价服从均匀分布的假设不符合实际情况，真实的概率分布可能满足正态分布或贝塔分布[20]。在很多情况下，报价更符合贝塔分布特征，其概率密度函数为

(12)

(13)

3 实例计算

3.1 样本分布

本文以西南某省的大型公路机电招标项目为例进行计算分析。该项目总投资约14亿元，分5个标段公开招标，评标办法规定根据各投标人的报价极值划分报价区间进行2次平均，乘以下浮率之后计算得到评标基准价，其中：式(2)中的权重系数β=0；式(3)中的扣分系数p=100,q=50,扣分临界值d=c=1；报价数据均来自于开标现场公布的信息。

首先确定报价的总体概率分布，对5个标段进行分布拟合，借助CrystalBall软件拟合投标报价方法[25]确定拟合分布和参数。综合Chi-square、A-D和K-S等3个检验水平，拟合得到Beta(2,3)分布是126个报价样本的最佳统计分布，具体拟合结果见图2。

图2 贝塔分布拟合结果

报价样本R的统计特征符合贝塔分布，而贝塔分布的概率取值范围为0～1，在确定好最高报价b和最低报价a之后，可由贝塔分布的概率密度函数随机生成仿真报价，即

R(σ,m)=a+(b-a)·betarand(x,γ,σ,m)

(14)

式(14)中：x=2；γ=3；σ为随机仿真样本的组数；m为每组报价数量。

结合仿真模型的影响因素和式(2)可知，评标基准价计算模型的样本参数包括招标控制价、报价数量、最高报价、最低报价、报价统计分布和下浮率(见表1)。在这6个参数中，假设招标控制价、最高报价和最低报价在开标之前是相对稳定的外部参数，招标控制价、报价数量和下浮率是仿真模型的重点参数。

3.2 仿真结果

一般在研究中将投标报价的上限b设定为最高投标限价(即招标控制价)，同时将投标报价与最高投标限价的比率作为仿真对象，使仿真模型标准化。但是，苏金霞等[20]研究发现，在实际评标过程中，报价上限值不等于最高投标限价。为减小仿真误差，在研究样本数据时寻找通用型报价的上限和下限，经过插值拟合之后发现，样本各标段的最高报价和最低报价都与该标段的最高投标限价线性相关，因此每次模拟的投标报价随机值都采用该取值范围的仿真函数(即式(14))生成。关于仿真次数，根据式(13)，将置信水平设为1‰(即准确率为99.99%)，查表得到置信度为0.001、自由度m=26的t值为3.435，代入样本方差之后得到仿真次数N≈25 000，设参数N=σ=25 000。

表1 仿真样本参数

以竞争最激烈的标段4为例，在仿真出N组评标基准价对应的最优报价之后，将报价划分区间数设为投标单位数，报价金额的经验概率密度和概率频数直方图见图3和图4。由图3和图4可知，概率密度有双峰特征，当报价金额为1.933 2亿元时，理论上概率密度最大，此时该报价即为最大概率值的最优报价。但是，标段4的评标基准价为1.955 0亿元，仿真结果与实际有1.1%的误差，第一中标候选人和第二候选人的报价金额分别为1.952 7亿元和1.951 8亿元。经分析，误差主要来源于样本近似服从统计分布的偏差。为消除该误差，设立一个调整系数，使仿真结果误差控制在0.1%左右。经测算发现，以报价取值划分区间为单位，调高3.1个单位之后仿真结果满足误差可忽略的精度要求。调整之后的标段4的仿真最优报价为1.954 7亿元，报价得分高于中标金额得分，报价收益多出20.09万元，仿真报价与评标价的接近度达99.98%。

同理可得到:标段1的仿真最优报价约为1.270 0亿元，报价得分高于中标金额得分，报价收益多出81.81万元，仿真报价与评标价的接近度达99.94%；标段2的仿真最优报价约为1.745 4亿元，报价收益多出38.56万元，仿真报价与评标价的接近度达99.78%；标段3的仿真最优报价约为1.870 9亿元，报价收益多出10.53万元，仿真报价与评标价的接近度达99.98%；标段5的仿真最优报价约为 2.144 2亿元，报价收益多出237.71万元，仿真报价与评标价的接近度达100.31%。各标段的仿真结果见表2，调整之后的仿真报价的得分均比第一中标候选人报价的得分高，中标概率更大，且利润更多。

图3 仿真报价概率密度

图4 仿真报价频数分布

表2 仿真最优报价汇总 元

设定5个标段的仿真最优报价为因变量，投标限价和下浮率为自变量，投标人数为25，得到仿真最优报价三维分布见图5,参数拟合结果见图6。由图6可知：最高投标限价决定了仿真结果的量级，而下浮率对仿真结果有微小调整的影响；不同投标人数量对应的仿真结果的变化趋势相同，在下浮率和最高投标限价都相同的条件下，投标人数较多的标段仿真最优报价较低，符合工程投标竞争越大，中标金额越低的实际情况。

图5 仿真最优报价三维分布

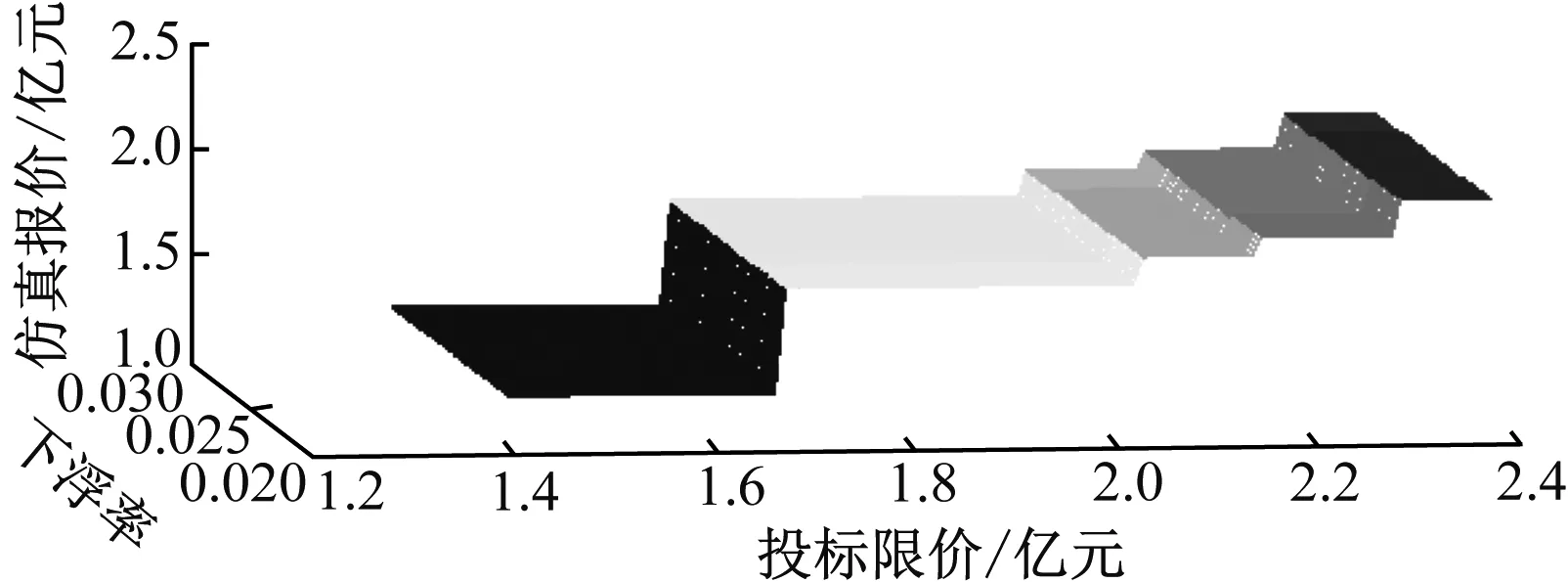
图6 仿真最优报价插值拟合

4 结 语

工程投标竞争符合非对称博弈过程，因此可建立博弈模型研究中标报价。本文在二次均值评标办法规则下运用蒙特卡洛仿真样本计算了投标报价样本的中标结果，仿真得到最优报价高度接近评标基准价，中标成功率得到明显提高。最优报价计算结果表明，在决定中标结果的5个主要参数中，招标控制价、报价数量和下浮率等3个参数是决定中标报价的关键因素，为提高投标中标率，需对这些参数进行建模分析。