基于历史航迹的船舶任意点到港的航线规划算法
段俊利,韩 懿
(中远海运科技股份有限公司,上海 200135)
0 引 言
近年来,随着科技的不断发展,基于互联网和大数据的陆地导航技术得到广泛应用,相关算法越来越成熟,导航精度越来越高,已能满足日常出行的导航需求。然而在水路运输领域,虽然国内外已有很多平台提供船舶自动识别系统(Automatic Identification System,AIS)实时船位和历史航迹查询服务,但基于互联网和大数据的海上导航技术应用较少。目前,全球的货物运输主要依靠船舶完成,海上航路边界模糊、水文气象变化频繁、海难事故频发和航行效率低下等问题日渐凸显。随着计算机技术的不断发展,航运业正逐渐朝着智能化方向发展,而航线规划是衡量船舶智能化水平的一项关键指标,对保障船舶安全、经济、快速航行具有重要作用。
在此背景下,为促进航运业的智能化发展,采用云部署的方式搭建互联网大数据平台,主要面向互联网公众提供航运服务,包括船位信息、航线信息和大数据板块,其中大数据包含船舶动态监控分析、风险监控分析和竞争对手分析等。为提供高效的服务,要求用户在利用该平台查询信息时能得到快速响应。目前该平台已存储18个月共计65亿条AIS轨迹数据,同时通过算法寻找港口之间的航线,得到了57 699条真实历史航线,涵盖16 512个港口对。本文基于海量的历史航线数据,开展航线规划算法的设计与试验分析,借鉴海量船舶的航行经验,保证船舶在满足一定准确性要求的前提下,实时获取航线规划结果。
1 国内外研究现状
目前,船舶驾驶员通常借助电子海图显示与信息系统(Electronic Chart Display and Information System,ECDIS)的辅助航线设计功能,参考导航库资料,根据个人经验进行航线规划,存在工作量大、航线的质量无法保证等缺点,很难满足现代航海的要求[1]。
近些年,航线规划问题得到了很多学者的关注。例如:刘敦伟[2]采用动力定位(Dynamic Positioning,DP)算法对大量AIS数据进行压缩之后,采用地理网格技术挖掘热点航迹段和典型航线,并基于典型航迹段数据库对任意点与港口之间的航线进行规划;姚肖肖等[3]基于DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法对压缩之后的轨迹点进行聚类,提取航路关键转向点,并构建无向网络图,采用蚁群算法求解出港口之间的最优安全航线;韩佳彤[4]基于大数据分析方法,提出一种船舶智能航线设计方法,通过基础电子海图地理信息数据,对船舶历史航线进行分析,计算出港到港、任意点到港和任意点到任意点的最优航线;DUCA等[5]提出一种基于KNN(K-Nearest Neighbor)分类器的航线预测算法,利用历史上的AIS信息了解过去的船舶航线,预测船舶在某一特定时间(包括30 min、45 min和60 min)之后的位置,通过对81艘船舶进行测试,取得了良好的效果;MAO等[6]采用Extreme Learning Machine模型,以某种特定的数据集分割方式将数据库中的一段轨迹切分为训练集和测试集,对给定时间点的轨迹进行预测,发现该算法对较短时间段的轨迹预测有较好的效果。
以上研究取得了很多成果,但现有的航线规划计算量大,很难做到实时、动态地完成航线规划,无法高效地将其应用到互联网大数据平台上。
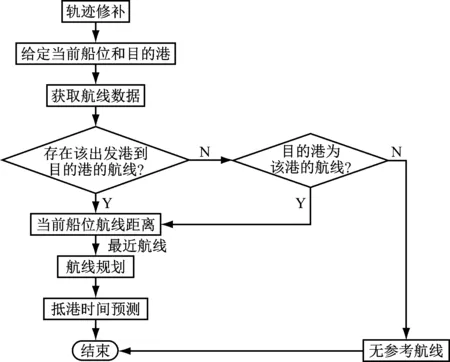
图1 航线规划算法流程图
2 算法流程设计
船舶AIS数据包含大量航迹信息,凝结了航海人员多年的航行经验。采用基于AIS动态数据的历史航线进行航线规划具有可行性。
受信号和设备的影响,AIS数据存在数据缺失的问题。为更好地利用历史航线进行航线规划,本文首先对原始的航线数据进行轨迹插值,并将其存储到数据库中;对于给定的船位和目的港,从修复之后的历史航线中寻找航程最短的航线,作为航线规划的结果;同时,基于当船舶当前的航速和剩余航程,完成抵港时间预测。航线规划算法流程图见图1。
2.1 AIS轨迹修复算法设计
AIS最基本的信息是由时间和经纬度位置组成的时空数据,此类数据可标记在地图上形成船舶航行轨迹。但是,受信号传输和AIS设备故障等因素影响,AIS时空数据会存在数据缺失的问题[7]。本文采用点到点的方式计算当前船位到历史航线的距离,若航迹存在数据缺失的问题,会使计算结果产生较大的偏差。为解决该问题,需设计一种AIS轨迹修复算法。目前,AIS轨迹修复方法有很多,既可采用聚类算法寻找相似的轨迹进行补全,又可采用插值的方式。本文采用插值的方式,将船舶航速和航向考虑在内[8],首先将AIS数据中缺失航段的左右两端A点和B点的经纬度坐标经过高斯-克吕格投影转换为高斯坐标(x1,y1)和(x2,y2)。利用A点的AIS动态信息得到插值点船舶位置的预测值为
(1)
式(1)中:v1、θ1和t1分别为A点的速度、航行方向和时间。利用B点的AIS动态信息得到插值点船舶位置的另一个预测值为
(2)
式(2)中:v2、θ2和t2分别为B点的速度、航行方向和时间。
对通过式(1)和式(2)得到的预测值(xi1,yi1)和(xi2,yi2)进行加权平均,权重根据A点和B点与插值点的时间差分配,时间差越小,权重越大,即
(3)
加权平均之后插值点的坐标为
(4)
对得到的高斯坐标进行高斯投影反算,即得到插值点的经纬度坐标。通过查看大量的船舶AIS时空数据发现,相邻的坐标点一般间隔10 min左右,本文对时间间隔超过20 min的航段采取每间隔10 min进行1次插值的方法,得到修复之后的完整航迹。
2.2 Hausdorff距离
为衡量修复之后的轨迹与原始轨迹的相似度,采用Hausdorff距离作为衡量标准。Hausdorff距离是2个点集之间相似程度的一种量度,设2个点集A={a1,…,ap},B={b1,…,bq},这2个点集之间的Hausdorff距离定义为
H(A,B)=max(h(A,B),h(B,A))
(5)
(6)
2.3 历史航迹查询与航线规划算法设计
在对原始的轨迹数据进行修复之后,要根据当前的船位和目的港选择合适的航线。由于历史航线众多,给定目的港的航线数据量较大,实时进行航线预测有一定的难度。为减少计算量,本文在查询给定目的地的航线时设置多个查询条件,以减少查询结果的数据量。若存在该船出发港至目的港的历史航线,则当前点到目的港的航线从此类航线中产生,否则再查询给定目的港的历史航线。给定目的港的历史航线遍布各个方向,基于当前的船位和目的港,方可大体上确定航线的方向,与该方向偏离较大的航线可忽略。根据当前的船位设定一个距离参数,在该距离形成的矩形范围内筛选航线。
给定距离的矩形范围,直接获得四点的经纬度,计算式为
(7)
式(7)中:φ和λ为船舶当前的经纬度位置;φN为矩形正北纬度;φS为矩形正南纬度;λE为矩形正东经度;λW为矩形正西经度;R为地球半径;d为用来寻找历史航线的矩形范围距离。
本文设定10~100 km距离划定当前船位的矩形范围,由此进行历史航迹查询。若根据10 km距离划定的矩形范围内包含历史航线,则查询停止,并从获得的航线中寻找最近航线;若根据10 km距离划定的矩形范围内不存在历史航线,则将距离扩展至20 km,以此类推。该方法只获取特定范围内的历史航线,能在较大程度上减少每条航线的轨迹数量,提高计算速度。
本文设计的算法的应用步骤为:
1)采用Python的pymysql模块连接数据库。
2)对于给定的船位经纬度(lon,lat)和目的港代码port_code,采用sql语句对附近航线矩形范围内的航迹进行查询;初始搜索的矩形范围设定为10 km,若该范围内存在航线,则查询停止,否则将搜索范围扩大至20 km,直至将矩形范围扩大至100 km或查询到航迹为止;若100 km范围内航迹数量为0,则说明未找到航线。
3)为方便计算船位到航线的距离,将上述查询得到的航线和航迹数据转换为Python常用数据处理模块Pandas中的DataFrame(DataFrame是一种类似表格的数据清洗常用的数据结构,包含一组有序的列,既有行索引,又有列索引)。
4)为计算当前船位到每条航线的距离,按line_ID(航线ID)对航线和航迹数据的DataFrame进行分组,新增一列来保存船位与每条航线上的轨迹点之间的距离,并在这些距离中找到最小值,作为当前船位到航线的最短距离。
5)计算距离船位最近的航迹点的剩余航线长度。
6)距离当前船位最近的航线即为要预测的航线,基于船舶航速和剩余航线的长度完成抵港时间预测。本文在试验时采用的航速是当前的航速,可根据实际情况选择不同的航速来对抵港时间进行预测。
3 试验分析
3.1 轨迹修复
从数据库中提取一条航线的航迹数据(见图2a),删除该航段中的20个估计点,采用插值方式进行轨迹修复,修复之后的航线见图2b。
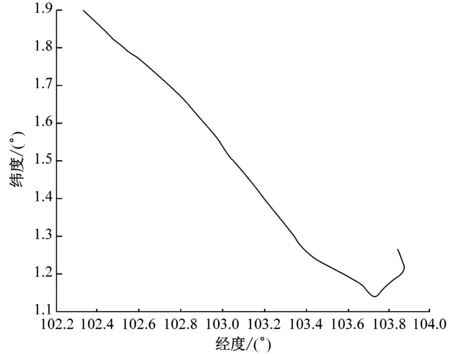
a)原始航线轨迹

b)插值之后的航线轨迹
由图2可知,航线修复前后的轨迹基本一致,两轨迹的Hausdorff距离为1.634 km。这说明本文采用的的插值方式对轨迹修复有明显的效果。本文设定Hausdorff阈值为20 km,超过该阈值则保留原轨迹,否则使用插值之后的轨迹。
3.2 航线规划
试验的运行环境为:联想笔记本;i7处理器;内存12 GB;64位操作系统;Win10家庭版。选取在航的水上移动通信业务标识码(Maritime Mobile Service Identify,MMSI)为477077700的集装箱船为研究对象,其当前的经纬度船位为(123.343 417,33.209 000),出发港为新加坡港,目的港为天津港。按历史航迹查询和选择算法共查询出13条航线,详细信息见表1,其中距离当前船位最近的航线ID是62338,此航线由上海到天津,与试验船舶的目的港相同。将规划的航线呈现在地图上,结果见图3,其中:实线部分为试验船真实航迹;虚线部分为使用ID为62338的航线预测的航迹。
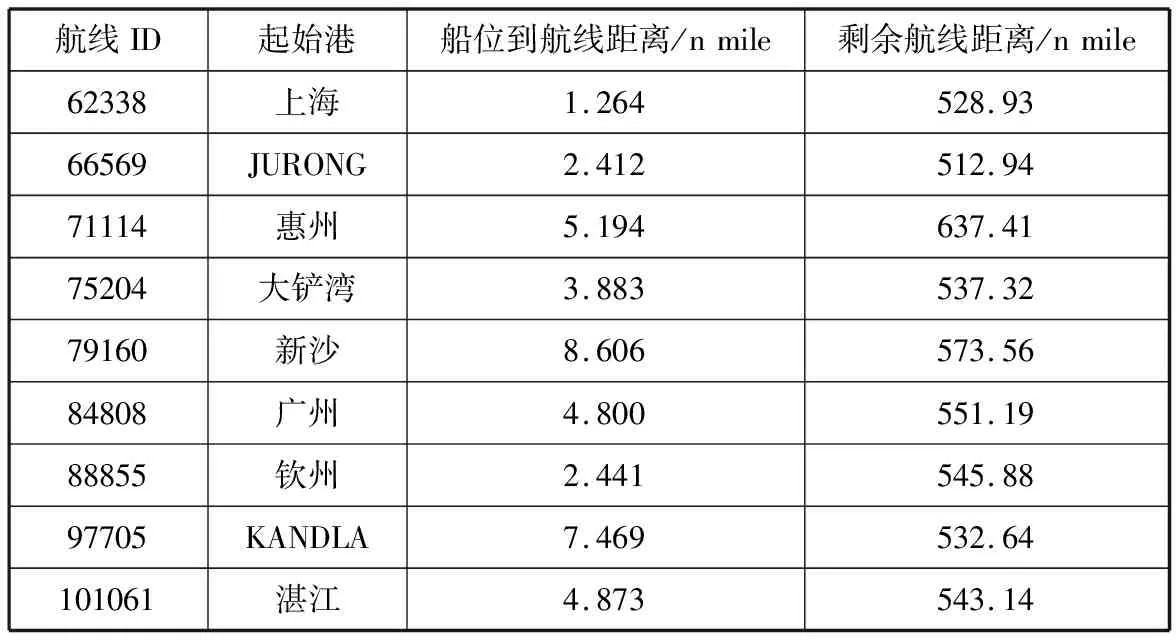
表1 试验船当前船位附近航线
船舶当前的航速为14.3 kn,当前的时间为2020-01-15T16:54:35,根据当前的航速预测的抵港时间为2020-01-17T07:55:00。船舶的实际航行路线见图4。图4中的黑点位置为该船当时的船位,从该点到天津港的航线与本文预测的航迹基本上无差异,抵港时间比预测的时间晚7 h左右,原因是算法所用航速为当前航速,而在实际航行过程中(特别是在进港和靠泊时),航速会发生变化,同时会受港口排班因素的影响,因此会产生一定的误差,该算法还有进一步优化的空间。
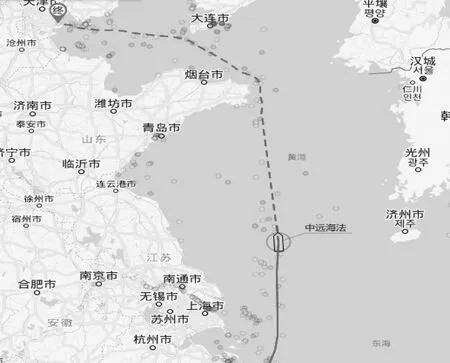
图3 航线预测
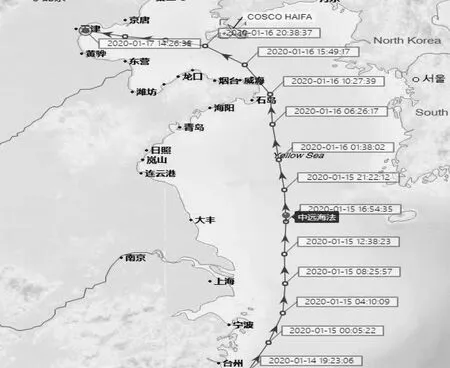
图4 试验船实际航行轨迹
按照上述算法设计,从历史AIS数据中随机抽取10艘船,对已完成的航次进行航线预测和验证,结果见表2。从表2中可看出,根据当前航速预测的抵港时间与实际时间存在一定的差异,误差基本上在1 d以内,且整体的运行速度基本上在3 s左右,能满足大数据平台的实时性要求。由于该算法是在单机环境下运行的,因此运行速度较慢,在大数据平台下,航线规划的速度基本上控制在1 s以内。

表2 10条历史航次的航线预测
4 结 语
本文对基于海量的AIS动态数据生成的历史航线进行了航线预测。在采用插值算法对原始航线数据进行修复之后,对于给定的当前船位和目的港,从数据库中获取合适的航线,并选择距离当前船位最近的航线作为最优航线,同时采用当前的航速预测抵港时间。试验结果表明,本文提出的航线规划算法能合理地对任意位置的船舶进行航线规划和抵港时间预测,误差基本上能控制在24 h以内,但在当前航速过低或过高的情况下,误差会偏大。
为避免利用当前的航速进行航线规划造成预测误差过大,可人工设定航速参数值,或对海量的AIS数据进行大数据分析,得到合理的航速范围。

