基于节点接触频率和持续时间率的数据转发算法

王 翟, 王青山, 王 琦, 任 璐, 程 曦, 章 翔

(合肥工业大学 数学学院,安徽 合肥 230601)

容迟网络(delay tolerant networks,DTN)是近年来广受关注的一类新兴的网络体系结构,是由Kevin于2003年在国际著名学术会议SIGCOMM上提出、基于节点间歇性连接而传输消息的无线网络。DTN有很多应用,如移动社交网络[1]、车载自组织网络[2]、卫星通信[3]、军事网络[4]等。随着智能手机等移动终端的使用,移动社交网络引起了人们的广泛关注。由于DTN网络中节点的随机移动、节点密度稀疏和电量有限等原因导致数据在传输过程中不能保证通信节点之间存在一条端到端路径,因此,合理的数据转发(路由)算法已成为DTN网络一个关键问题,如何在保证信息传递成功的基础上减少信息在网络中传递延迟是衡量DTN性能的一个重要指标。

针对DTN数据转发算法优化问题,相关研究一般采用“存储-携带-转发”的数据传输策略[5],其中主要工作可以分为基于复制的数据转发算法[6-7]和基于效用的数据转发算法[8-11]。基于复制的数据转发算法主要思想是传输消息时产生多份拷贝信息,通过增加网络中的信息拷贝数目来提高数据传输率,如 Epidemic算法。基于效用的数据转发算法是利用网络中节点的状态信息来决定节点相遇时是否转发消息;它通过建立一个函数来估计每个节点的效用,节点的效用越高,则遇到目的节点的概率越大。

然而，以往基于效用的转发算法主要利用节点的历史状态信息来估计节点的效用;本文则是通过预测节点未来相遇状态信息来估计节点的效用,即从节点间接触频率和持续时间率2个重要指标出发,设计基于节点接触频率和持续时间率的数据转发算法。节点相遇持续时间率,即相遇时间与总时间的比值。网络中3个节点j、k、l在时间区间[0,T]内与数据包d的目的节点D相遇情况如图1所示。

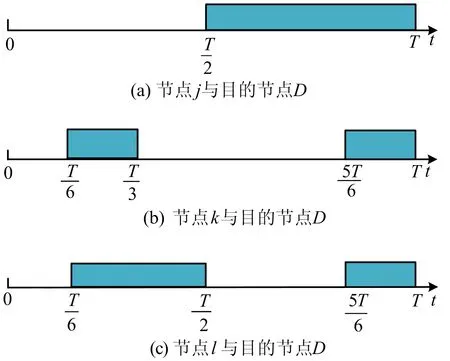
图1 节点j、k、l在[0,T]内与目的节点D相遇情况

假设节点i是网络中携带数据包的节点,fj,D为在[0,T]内节点j与节点D的相遇频率,cj,D为在[0,T]内节点j与节点D相遇持续时间率。在图1a中,节点j与目的节点D在[T/2,T]内一直相遇,总共相遇1次,可得fj,D=1,cj,D=1/2。在图1b中,节点k与目的节点D在[T/6,T/3]∪[5T/6,T]内一直相遇,总共相遇2次,可得fk,D=2,ck,D=1/3。同理,在图1c中,可得fl,D=2,cl,D=1/2。

假设数据包携带者i与中继候选节点j、k、l在T时间内任何时间点相遇都是等可能的,当节点i与节点j、k、l相遇时,它会选择拷贝或者不拷贝数据包给节点j、k、l。如果拷贝数据包,那么可以利用图1节点j、k、l与目的节点D的相遇情况来求出传递延迟,从而判断哪个节点作为中继节点最好。由于节点i与节点j、k、l相遇时间是随机的,则概率密度函数为1/T。假设在t时刻节点i和节点j相遇,而且节点i将数据包d拷贝给节点j,节点j可能需要一段时间才能与目的节点D碰面。从t时刻开始到目的节点D收到来自节点j的包所经历的时间记为延迟Yi,j,D,可以得到:

同理,可求得：

由图1a、图1c计算可知,当节点间的接触时间率一样,接触频率越大,延迟越小。由图1b、图1c计算可知,当节点间的接触频率一样,接触时间率越大,延迟越小。因此,节点间的接触频率和时间率同时是影响延迟的重要指标。

1 网络模型

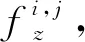
(1)

为了求S(f,c)的最小值,分别对(1)式中f、c求一阶偏导并令导数为0,得到:

(2)

(3)

(4)

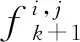
2 CFTDF算法

本文提出了一种基于节点接触频率和持续时间率的数据转发(contact frequency and time ratio-based data forwarding,CFTDF)算法。该算法以历史上Tz(1≤z≤k)时间区间内节点间的接触频率和持续时间率为基础,对下一时间区间Tk+1内节点间的接触频率和持续时间率进行预测,并据此定义节点间的活性(activity)作为选择中继节点的标准。

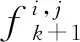
0≤w≤1

(5)

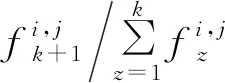
CFTDF算法如下:在Tk+1内,当携带数据包的节点i与没有数据包拷贝的节点j相遇时,若节点j是目的节点D,则直接转发数据包给目的节点;否则,若节点j与目的节点D之间的活性大于节点i与目的节点D之间的活性,则节点i拷贝数据包给节点j;若节点j与目的节点D之间的活性小于或者等于节点i与目的节点D之间的活性,则节点i不转发数据包给节点j。

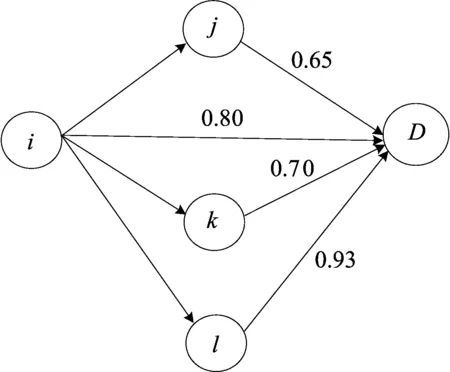
图2 CFTDF算法示例

3 模拟实验结果和分析

本文用C++语言开发了一个模拟器来研究CFTDF算法、Epidemic算法[6]及间接概率转发(probability-inferred forwarding,PIF)算法[12]在移动社交网络中的性能。

选择Infocm06[13]节点移动轨迹作为节点移动模式,它是由2006年在西班牙巴塞罗那召开的Infocom会议上78个志愿者通过携带imote设备采集得到的数据;另外,在会场不同区域布置了20个固定的imote设备作为不动节点。实验随机产生200对源节点和目的节点进行通信。本文主要对上述3种算法比较以下3个方面性能:

(1) 传递率,即目的节点成功收到数据包数目与源节点产生数据包数目的比值。

(2) 传递延迟,即数据包从源节点成功到达目的节点所经历时间的平均值。

(3) 拷贝数目,即数据包在整个网络中复制数目。

将前3 600×48 s节点间相遇情况作为历史记录,划分为4个相等时间区间,分别记为T1、T2、T3、T4,此后在长度3 600×12 s的T5内发包。

实验1 数据包的生存时间 (time-to-live,TTL)长度对算法性能的影响。数据包的TTL长度从6 h变化到36 h,实验结果如图3所示。

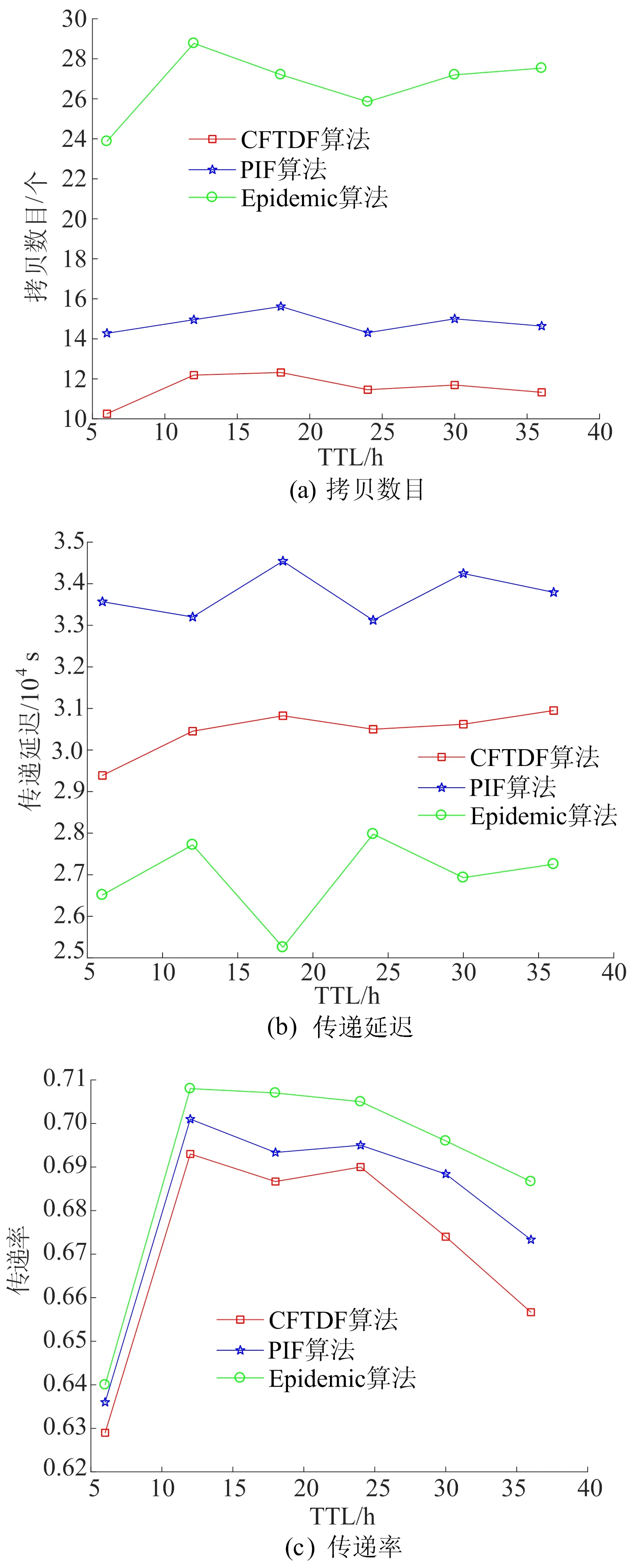
图3 TTL对算法性能的影响

由图3a可知,3种算法在数据包的拷贝数目上差异较大,Epidemic算法拷贝数目最多,PIF算法次之,CFTDF算法最少。具体地,CFTDF算法比PIF算法平均低10.4%,比Epidemic算法平均低57%,这主要是由于CFTDF算法在选择转发节点时条件较为苛刻,导致选择的转发节点个数较少,即开销较小,优化效果比较明显。

由图3b可知,Epidemic算法传递延迟最低,PIF算法最高;CFTDF算法比PIF算法平均低13.6%,延迟效果较好。这是由于CFTDF算法在选择中继节点时会选择与目的节点接触次数较多、接触时间较长的那些节点,尽可能快地将数据包传递到目的节点。

由图3c可知,3种算法的传递率大致相同。

实验2 参数w对CFTDF算法性能的影响。通过改变(5)式中w的值来研究其对CFTDF算法性能的影响,实验结果如图4所示。

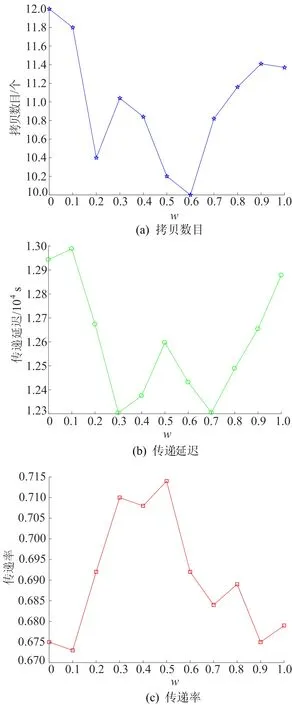
图4 w值对算法性能的影响

由图4a可知,w为0.3～0.6时,拷贝数目最少,即网络资源消耗最少;当w取2个极端值0或1时,拷贝数目较大。

由图4b可知,w为0.3、0.4、0.6、0.7时都可以获得较小的传递延迟;当w取2个极端值0或1时,传递延迟较大。

由图4c可知,当w=0.3时,传递率高达0.71,效果较好;当w为0或1时,传递延迟相对较低。

通过实验可以得出,参数w对结果影响较大,而且综合考虑接触频率和持续时间率的效果比单独考虑其中一方面要好。

4 结 论

本文在容迟网络中提出了一种基于节点接触频率和持续时间率的数据转发算法(CFTDF算法)。该算法通过节点间历史相遇信息来预测节点间未来接触频率和时间率,并由此定义节点间活性,然后根据相遇节点分别与目的节点活性值大小来选择合适中继节点,从而减少传递延迟。仿真实验结果验证了该算法能够在拷贝数目和传递延迟方面取得比较好的效果。如何进一步通过研究节点的历史相遇情况来推测节点未来相遇分布情况,从而精确估计节点活性,是下一步研究方向。