偏振编码BB84系统在OPGW光缆舞动情况下的稳定性

曾 荣, 马媛媛, 张传虎

(1.全球能源互联网研究院有限公司,江苏 南京 210003; 2.信息网络安全国网重点实验室,江苏 南京 210003; 3.安徽问天量子科技股份有限公司,安徽 芜湖 241000)

量子密钥分配技术是一种先进的理论上可证明安全的异地密钥共享技术。它的可证明安全性是由量子信息物理原理保证的,相比于经典对称密码或非对称密码体系,它的安全性不依赖于任何计算复杂度算法,因此成为在量子计算机时代最有前途的保密通信方法之一[1]。自从1984年Bennett和Brassard提出第一个量子密钥分配协议开始[2],量子密钥分配技术便开始迅速地发展,世界各国都纷纷进行了相关的实验与研究,著名的网络有美国国防高级研究计划局(Defense Advanced Research Projects Agency,DARPA)量子网络[3]、欧洲基于量子密码的安全通信(Secure Communication based on Quantum Cryptography, SECOQC)网络[4]等。我国于2016年成功发射墨子号量子科学实验卫星(简称“墨子号”)[5],2017年成功实现了京沪干线量子通信。

随着量子密钥分配技术逐渐走向实用化,如何构建海陆空一体化的量子密钥分配网络越来越受到了专家学者以及各级政府的关注。一般认为,量子密钥分配全球网络的建设需要包括以量子卫星为载体的长距离密钥分配、城际和城域量子密钥中短程通信网络,以及到户的量子密钥接入网络等部分[6]。而光纤介质特有的可拓展性和稳定性使其成为城际以及城域量子密钥分配网络中非常重要的信道。随着经典通信的快速发展,一张完善的光纤通信网络已经在各大城市之间建立起来,如何使得量子密钥通信系统在这些光纤信道中稳定的运行就成为了构建城际以及城域量子密钥分配网络急需解决的问题。

现有的经典通信光纤信道按照光纤所处的位置,可以分为地埋光纤信道以及架空光纤信道2种[7]。地埋光纤信道是指被埋在地面以下采用光纤通信的信道,而架空光纤信道则常常集成在架空光缆之中,与输电线路合成在一起,悬挂于电塔之间[8]。相比于地埋光纤信道,架空光纤信道更容易受到外部环境中温度变化、空气流动甚至于周围电场等的影响。因此,如何使得量子密钥分配系统可以稳定地运行于架空光缆之中成为一个重要的问题。

本文通过实验,模拟了由于光纤复合架空地线(optical fiber composite overhead ground wire,OPGW)周围空气变化所造成的光缆舞动对架空光纤中偏振态所引起的变化,并且结合偏振编码BB84系统的特点[9],对这些偏振变化进行了分析,最后根据实验结果给出了在特定光缆舞动振幅下,偏振编码BB84系统所需要的偏振控制最小时间间隔。本文工作可以作为运行于架空光缆中偏振编码BB84系统的参考,并且对下一步架空光缆中量子密钥分配系统标准的建立有一定的参考意义。

1 实验过程与结果

光缆舞动模拟实验简图如图1所示。光缆舞动是一种常见的光缆在高速稳定的空气流动下的光缆震动现象[8,10],造成这种现象的风速一般为25～65 km/h。其一般产生震动的主轴为垂直方向,且伴随着较大的震动幅度和较小的震动频率。其震动幅度一般为5～300倍的光缆直径,震动频率为0.08～3.00 Hz。

实验中利用1束脉冲半导体激光光源(81960A,Agilent Technologies)产生激光光束,该光源产生的脉冲波长为1 550 nm;随后将该激光光束射入到一段OPGW光缆中,OPGW光缆搭建在2条模拟电塔上,并且光缆两端连接促动器,用以模拟不同震动幅度的光缆舞动现象;在OPGW光缆的另一端,连接偏振分析仪(N7788B,Agilent Technologies)用以分析光缆出射偏振态,偏振分析仪以斯托克斯矢量的形式记录其入射光的偏振态,随后利用电脑记录出射偏振态以供下一步的分析。斯托克斯矢量表示为(S0,S1,S2,S3)[11],其中S1、S2、S3分别为入射偏振态在庞加莱球上的坐标,对于完全偏振态来说,S0恒等于1,因此在后面的计算分析中,均省略S0进行计算。

实验模拟了不同光缆长度下光缆舞动的情况,光缆舞动频率为1.00 Hz,振幅为600 mm,长度分别为75、150、300、825 m。在4种架空光缆长度下光纤内的偏振变化时域波形如图2所示。

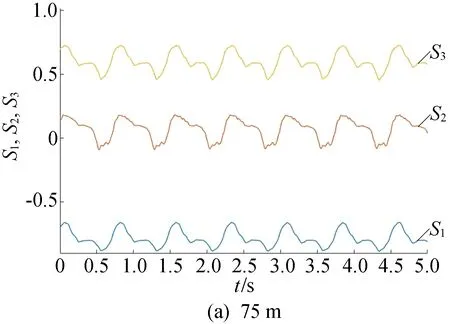
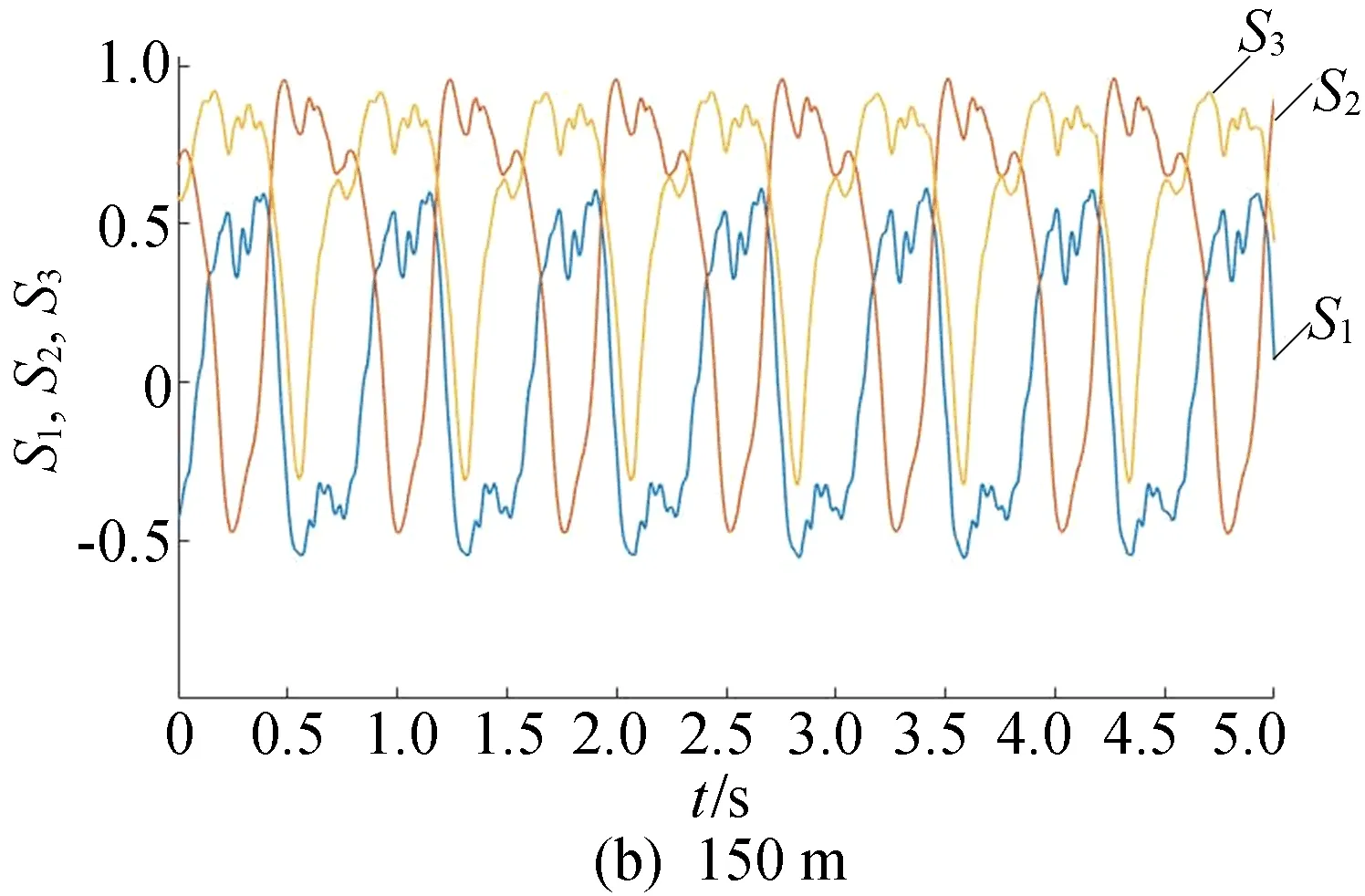
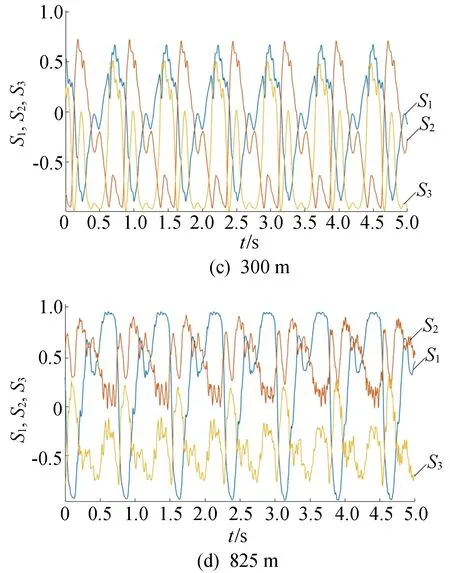
图2 不同光缆长度下架空光纤在舞动情况下的偏振变化

从测量结果可以看出,OPGW光缆中的偏振态变化周期是和光缆舞动频率保持一致的,在4种情况下均为1.00 Hz。随着光缆长度的增加,偏振态变化幅度也在逐渐变大,且两者之间存在着类似线性增长的关系。由此可知,光缆舞动对架空光纤中偏振态的影响比较突出。

2 分析模型与结果讨论

这里考虑偏振编码BB84系统量子比特误码率(quantum bit error rate, QBER)[12]与信道中偏振态变化情况的关系,为了方便计算,以BB84系统中2个非正交基中的一个基为例进行计算,另外一个基的计算方法完全相同。假设在t0时刻,量子密钥分配系统发射端Alice和接收端Bob之间的偏振坐标系完全对准,此时系统中QBER为0;假设量子密钥分配系统中QBER的增加原因只包括信道中偏振态的变化。在t0时刻,架空光纤出射偏振态可设为|φt0〉,经过t时间后,架空光纤出射偏振态变为|φt0+t〉,此时可得:

|φt0+t〉=α|φt0〉+β|φt0〉⊥

(1)

其中,|φt0〉⊥为与|φt0〉垂直的偏振态;α、β分别为|φt0+t〉在|φt0〉、|φt0〉⊥上投影的复振幅,并且满足|α|2+|β|2=1。QBER计算公式为:

(2)

其中,RQBE为量子比特误码率。

由于在本文实验中,架空光纤中的偏振态是由斯托克斯矢量表示的,需要考虑QBER和斯托克斯矢量之间的关系。假设态|φt0〉、|φt0〉⊥及|φt0+t〉对应的斯托克斯矢量分别为St0、St0⊥、St0+t。不失一般性,由于相互垂直的偏振态在庞加莱球上的连线必过球心,因此一定会存在一个坐标变换U使得USt0=[1 0 0]T、USt0⊥=[-1 0 0]T同时成立。根据斯托克斯矢量的定义,在相同的变化下一定存在:

USt0+t=

[|α|2-|β|22Re(αβ*) 2Im(αβ*)]T

(3)

因此有:

(4)

联立(2)式、(4)式可得:

(5)

下面定义误码漂移时间参数τ来表征QBER从0增加到它的阈值eth所需要消耗的时间。根据(5)式,τ满足:

(6)

利用(6)式对架空光纤中的偏振态数据进行分析后可得到平均误码漂移时间〈τ〉,它的含义为对于运行在特定架空光纤上的偏振编码BB84系统,平均每经过〈τ〉时间就必须进行一次偏振控制才能保证系统运行正常。〈τ〉越小,表示对于该条架空光纤来说,量子密钥分配系统越不稳定。

根据上述分析模型,计算当eth=3%,架空光缆长度为825 m时,偏振量子密钥分配系统的平均漂移时间,其分布直方图如图3所示。从图3可以看出,绝大部分漂移时间在0.01～0.02 s之间,而平均漂移时间则为0.022 8 s。

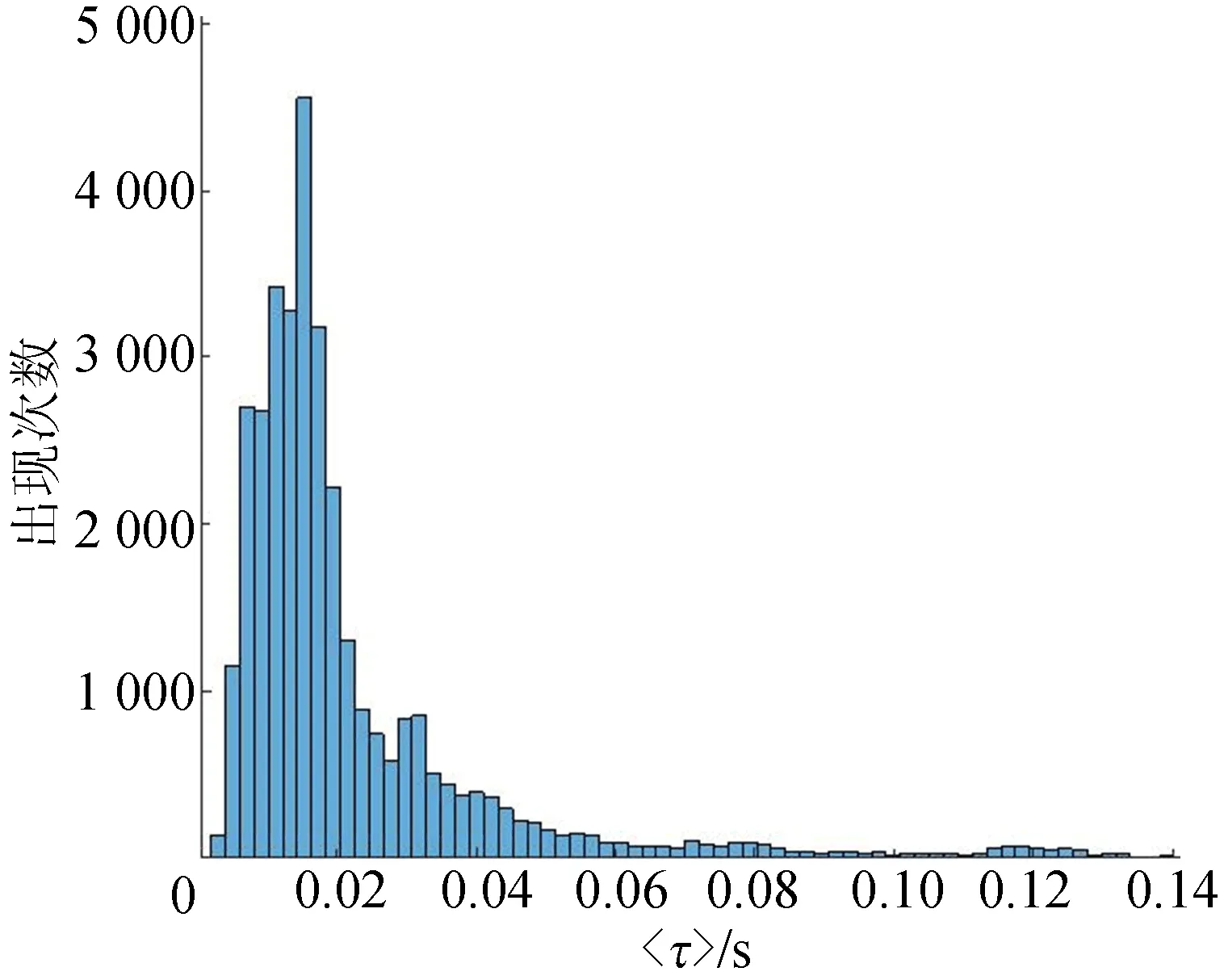
图3 平均误码漂移时间分布直方图

根据实验测量到的偏振态数据,绘制在不同eth、不同架空光缆长度下〈τ〉变化曲线,结果如图4所示。

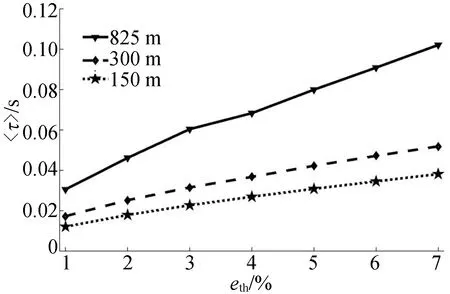
图4 平均误码漂移时间变化情形

在eth取值为1%、3%、5%下对偏振数据进行分析,从分析结果可以看出,光缆舞动会对量子密钥分配系统造成巨大的影响。以eth=3%,光缆长度为825 m为例,系统平均每经过0.02 s就必须中断1次来进行偏振控制,这对于量子密钥分配系统是一个不小的负担。从分析结果可知,在相同的舞动幅度下,eth值越低,则对应的平均漂移时间也越低,此外平均漂移时间也会随着架空光缆舞动长度的增加而减小。考虑到现有中断式量子密钥分配系统的架空光缆长度实际上要远远大于825 m,甚至达到几十甚至上百千米,如果这段光缆中出现长距离的光缆舞动现象,那么偏振编码量子密钥分配系统平均误码漂移时间有可能达到μs量级,根据现有量子密钥分配系统中偏振控制系统的速度[13],在这种情况下,偏振编码量子密钥分配系统有可能无法工作。因此,为了保证偏振编码量子密钥系统的稳定运行,架空光缆舞动现象是需要极力避免的。

3 结 论

本文通过室内实验模拟了不同长度架空光缆的光缆舞动现象,记录了在不同情况下架空光纤中的偏振态变化情况,并且结合偏振编码BB84系统的误码分析模型具体分析了光缆舞动现象对该量子密钥分配系统的影响。由分析结果可知,舞动现象造成的影响非常巨大,并且随着误码率阈值的降低,以及架空光缆距离的增长,平均漂移时间几乎是线性下降的。因此,光缆舞动现象对量子密钥分配系统的影响巨大,在实际电网架空光缆偏振编码量子密钥网络中,这种现象是需要极力避免的。