非线性频偏FDA对测向系统的欺骗研究
陈楚舒, 盛 川, 谢军伟, 王 博, 单泉铭
(空军工程大学防空反导学院, 西安, 710051)
与相控阵雷达不同,FDA可实现具有更高自由度的时间-距离-角度三维相关波束指向[1-2]。随着FDA研究的深入,涌现出大量关于FDA的研究文献[3-8]。如何干扰、破坏敌方雷达探测系统的测向、测速以及目标定位过程从而有效掩护我方目标,是雷达电子战研究中的重要课题[9-10]。文献[11]从主瓣压制、主瓣欺骗、副瓣压制、副瓣欺骗、组合干扰5个方面对干扰机的干扰效果进行了仿真评估。现有文献中较少有关于FDA对敌方雷达探测系统干扰效果的研究。文献[12]概述了FDA雷达当前的研究现状、发展和成就,及其在电子对抗(Electronic Countermeasures,ECM)和电子反对抗(Electronic Counter-Countermeasure,ECCM)技术领域应用的可能。文献[13]分析了FDA对测向时差组合定位系统的干扰效果。文献[14]分析了FDA对相邻天线比幅单脉冲测向系统的欺骗效果。但上述文献都是基于采用固定频偏增量的FDA结构,没有考虑FDA的方向图距离-角度耦合。本文将4种非线性的频控函数引入FDA,在实现方向图距离-角度解耦的基础上,仿真分析了采用非线性频偏的FDA对基于相位法测向的干涉仪系统的角度欺骗效果。
1 模型假设
图1为基本FDA的阵列结构[1]。

图1 基本FDA的阵列结构
设载波频率为f0,阵元n的辐射信号频率为:
fn=f0+Δfn=f0+nΔf,n=0,1,…,N-1
(1)
窄带条件下,阵元n的发射信号表示为:
sn(t)=exp(j2πfnt),n=0,1,…,N-1
(2)
阵元n发射的信号到达远场观测点(R,θ)的信号表达式为:
(3)
式中:rn=R-ndsinθ,R为参考阵元到目标点的距离;d为阵元间距;c表示光速。
远场观测点(R,θ)处的电场强度的总和为[1]:
(4)
取γ=Δft+(f0dsinθ)/c-ΔfR/c,由于f0≫NΔf,式(4)可化简为:
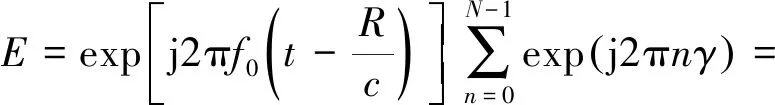
(5)
取阵列因子AF(t,R,θ)为:
(6)
取相位方向图为:
(7)
由式(6)可得FDA的时间、距离、角度周期性计算公式:
(8)
(9)
(10)
由式(8)~(10)可知,当距离R和角度θ固定时,方向图时间维的最小周期为1/Δf;当时间t和角度θ固定时,方向图距离维的最小周期为c/Δf。
在雷达参数中,波束宽度会对方向图增益的大小产生直接影响,进而影响阵列的扫描范围、阵列孔径等参数的限制条件。与相控阵波束宽度仅与阵元数、阵列孔径及波长相关不同,当波束指向阵列法线方向时,FDA的波束宽度还与频偏、时间及目标距离有关。由式(6)得归一化的方向性函数:
(11)
式(11)为sinc函数,当sinx/x=0.707时,x=±0.443π,由此可求出FDA波束的半功率宽度:
(12)
当Δf=0时,式(12)等效为相控阵的半功率波束宽度。当目标位于R0、θ0位置时,FDA的波束宽度为:
θ0.5-FDA=
(13)
图2~3分别为二维平面内相控阵与FDA的发射方向图,仿真参数见表1。
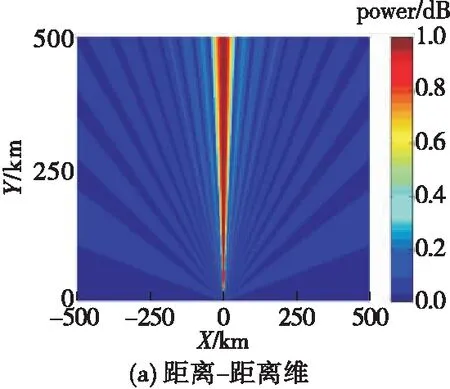

图2 相控阵的发射方向图
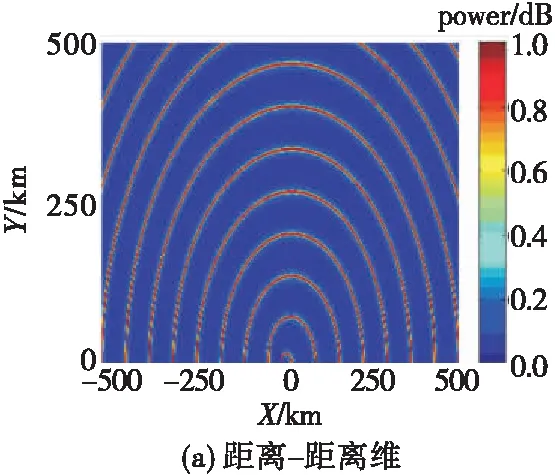

图3 FDA的发射方向图

表1 FDA雷达仿真参数
图2中,相控阵的波束指向为阵列法线方向。以距离为坐标,FDA的发射方向图为图3(a)中的环型;以角度和距离为坐标,FDA的发射方向图为图3(b)所示的S型。图4为PA与FDA在固定角度位置处其波束指向随距离的变化。由图4可知,PA的波束指向仅与角度相关而与距离无关,而FDA的波束指向具有距离-角度二维相关性。在同一角度不同距离上FDA的波束指向存在较大偏移,存在对侦查方实施角度欺骗的可能。

图4 固定位置处PA与FDA的距离维波束指向
2 FDA方向图的距离-角度解耦
文献[15]指出FDA发射方向图会出现距离和方位角响应的耦合问题,因而无法利用其无模糊地实现目标距离和方位的二维联合估计。针对如何选择频偏从而改进FDA的阵列性能,文献中展开了大量研究[16-17]。
采用非线性频偏增量的情况下,图1的FDA相邻阵元间频偏为Δfn,第n个阵元的载频为:
fn=f0+Δfn,n=0,1,…,N-1
(14)
则其发射波束方向图可以表示为:
p(t,θ,R)=
(15)
考虑对阵元间频率进行编码:Δfn=xnΔf,xn表示编码系数。此时,第n个阵元与参考阵元的相位差为:
Δψn=ψ0-ψn=
(16)
式中第1项为由距离差引起的传统相控阵的相移量,将式中后2项视为虚拟相移量,令:
(17)
式中:θ0代表实际的波束指向。由于f0≫(N-1)Δf,省略式(17)右端第2项可得:
(18)
从而得到波束指向角θ0的计算公式:
(19)
基本FDA相当于编码系数xn=n的情况。本文4.2节中对不同非线性频偏增量形式的FDA发射方向图特性展开了对比分析:当xn=log(n+1)时得到对数FDA(log-FDA),当xn=sin(n)时得到正弦FDA(sin-FDA),当xn=1/(n+1)时得到倒数FDA(reciprocal-FDA),当xn=n2时得到平方FDA(square-FDA)。
3 对干涉仪的角度欺骗分析
3.1 基于欧拉公式的FDA阵列因子
基于图1所示的阵列模型,当采用非线性频偏时,阵元n的辐射信号频率如式(14)所示。此时,无法通过级数求和得到如式(6)的sinc形式的阵列因子。本文通过欧拉公式对式(5)所示的场强进行化简[18-19]:
(20)
式中:
(21)
基于欧拉公式的FDA阵列因子为:
AF2(t,R,θ)=
(22)
式(23)为基于欧拉公式的FDA相位方向图:
Φ2=
(23)
3.2 FDA对干涉仪测向的角度欺骗
图5的基本干涉仪具有2个匹配良好的天线[18]。将干涉仪天线接收到的高频信号经与同一本振信号差频后在中频比相,根据得出的相差即可计算出发射机所在的方向。比相器输出的相差与信号到达角的关系为:
(24)

图5 一维单基线相位干涉仪
根据干涉三角法即可得到信号相对于干涉仪天线视轴的到达角:
(25)
干涉仪与图1的FDA在X-Y平面内的位置关系见图6。

图6 FDA与干涉仪的位置关系
电磁波自FDA径向传播,远场条件干涉仪可近似为点目标。设远场条件下干涉仪接收机2的坐标为(xG,yG),则接收机1的坐标为(xG+B,yG)。根据式(23)可得FDA的辐射信号在干涉仪2个天线位置处的相位:
(26)
式中:
(27)
比相器输出的相差为:
ψ=Φ22-Φ21
(28)
根据相差可以计算出发射机信号的到达角:
(29)
由信号到达角可以进一步计算出虚拟发射机在X轴的位置坐标:
x=xG-yGtanβ
(30)
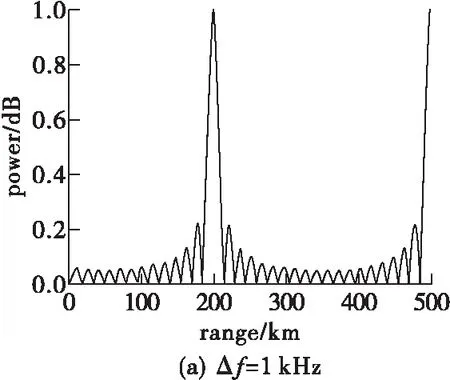
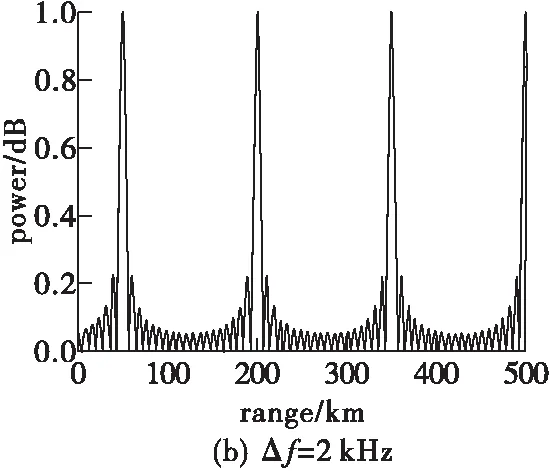
式中:yGtanβ为干涉仪计算出的辐射源所在方向与X轴交点(即为虚拟发射机位置)到干涉仪距离的绝对值。当xG>yGtanβ时,交点在X轴正半轴,x1=xG-yGtanβ,即为虚拟发射机位置坐标;当xG 假设目标位于(200 km,30°),其余仿真参数如表1所示。图7仿真了Δf取不同值时FDA发射方向图特性的不同。图7中4个子图的距离维最小周期分别为300 km,150 km,100 km,66.7 km,可知都符合式(10)中T=c/Δf的结论。当频偏增量Δf的取值增加时,由式(10)可知方向图距离维的周期性增加;由式(13)可知FDA的3 dB波束宽减小,扫描精度增加。图7中存在的多值性问题是由于线性频偏增量Δf与阵元间距d的线性递增同步导致的。 图7 Δf取值对FDA距离维周期性的影响 假设目标位于(200 km,30°),其余参数见表1。图8中的FDA分别采用对数函数、三角函数、倒数函数以及指数函数4种不同形式的非线性频偏增量,打破了频偏增量Δf与阵元间距d的线性递增的同步关系。图9对比了相控阵,基本FDA,sin-FDA,log-FDA,倒数FDA以及平方FDA共6种阵列在目标位置处的角度维波束宽度,图10~11对比了这6种阵列在目标位置处的距离维波束宽度。 图8(a)和图8(b)能够在目标位置处形成能量相对集中的“点状”波束,能够消除基本FDA发射方向图中的距离-角度耦合。倒数形式的频偏增量文献中较少采用,如图8(c)所示,由于其波束在距离维上存在较长的拖尾,在实际中的应用价值也较低。图8(d)的指数形式的频偏增量在远场条件下存在失效的问题[17]。由图9可知6种阵列在目标位置处的角度维波束宽度完全相等。但在目标位置处的距离维上,如图10所示,不同结构的波束形状存在较大差异。其中,相控阵的波束指向与距离无关,在抑制距离相关性干扰方面存在不足;倒数FDA波束主瓣在距离维存在较长的拖尾,分辨力较低,实际中应用价值较低;log-FDA与sin-FDA的性能相对较好,后续仿真主要基于这2种结构进行。 图8 不同非线性频控函数FDA的发射方向图 图9 6种阵列在目标位置处的角度维波束宽度 图10 5种阵列在目标位置处的距离维波束宽度 图11 平方FDA在目标位置处的距离维波束宽度 图12仿真了当干涉仪Y轴坐标yG=5 km,基线B=0.1 m,其余仿真参数见表1时,3种FDA对干涉仪测向的影响。图中横坐标为干涉仪的X轴坐标xG,纵坐标为根据干涉仪测向原理得到的虚拟发射机在X轴的交点坐标。图12中的2条红色横线为FDA参考阵元(X轴坐标为0)及阵元N(X轴坐标为(N-1)d)在X轴的坐标,当虚拟发射机在X轴的交点坐标落入这个区域时,无法对干涉仪测向实现有效的影响。基本FDA的交点坐标曲线最为平滑,角度欺骗效果最佳。log-FDA、sin-FDA的虚拟发射机交点坐标始终在实际阵列位置附近,偏离量较小。考虑到基本FDA方向图中的距离-角度耦合,后续只对log-FDA及sin-FDA展开分析。 图12 3种FDA对干涉仪测向的影响(yG=5 km) 图13仿真了当干涉仪Y轴坐标yG=5 km,基线B=0.1 m,其余仿真参数如表1时,Δf取值对干涉仪测向性能的影响。 由图13可知,在一定范围内,FDA对干涉仪测向的影响随着频偏增量Δf的增大而增强。远场条件下,虚拟发射机在X轴的交点坐标逐渐偏离FDA坐标位置,可以实现有效的角度欺骗,其中log-FDA的影响效果整体上优于sin-FDA。 图13 Δf取值对2种FDA角度欺骗效果的影响 图14仿真了当干涉仪Y轴坐标yG=5 km,基线B=0.1 m,其余仿真参数见表1时,阵元间距d对干涉仪测向性能的影响。由基准载频f0=1 GHz可知波长λ=0.3 m。图14(b)中d=0.45λ,阵元N的X轴坐标为2.565;图14(c)中d=0.9λ,阵元N的X轴坐标为5.13;图14(d)中d=1.9λ,阵元N的X轴坐标为10.83。由图14可知,阵元间距d增大时,log-FDA始终比sin-FDA的性能更好,且2种阵列结构在远场位置处的坐标偏移量随着阵元间距d的增大而增加。 图14 阵元间距d对2种FDA角度欺骗效果的影响 FDA雷达能够产生距离-角度-时间相关波束,在雷达目标的距离-方位角联合估计、射频隐身以及前视探测与成像等领域都有广阔的应用前景。本文仿真分析了log-FDA、sin-FDA、reciprocal-FDA和reciprocal-FDA中log-FDA与sin-FDA能最有效地消除基本FDA发射方向图中的距离-角度耦合。进而分析了远场条件下log-FDA、sin-FDA可对干涉仪测向产生欺骗。在此基础上,仿真分析了阵列载频和阵元间距这2个重要参数对欺骗效果的影响,得出以下结论:FDA对干涉仪测向的影响随着频偏增量Δf的增大和阵元间距d增大而增强,且log-FDA始终比sin-FDA的性能更好。4 仿真分析
4.1 Δf取值对FDA方向图特性的影响


4.2 不同非线性频偏FDA的发射方向图对比

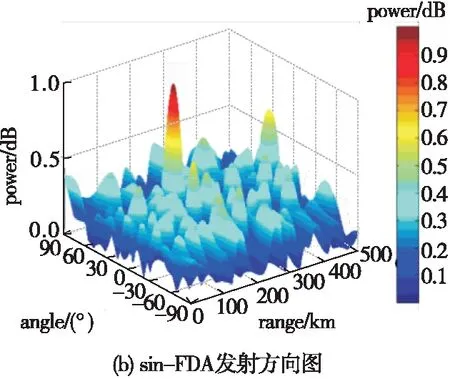
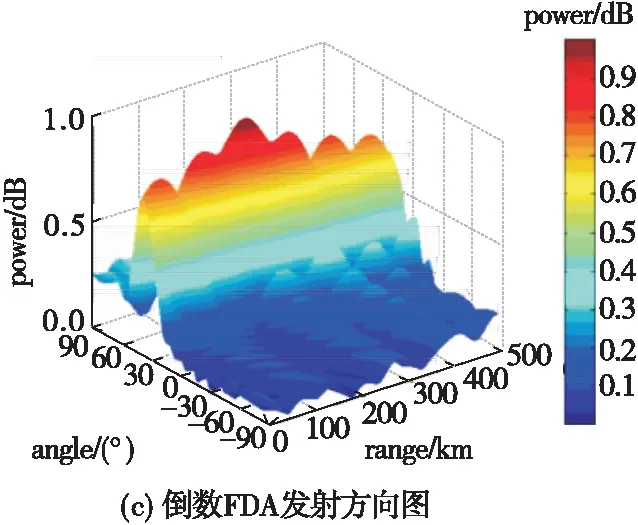

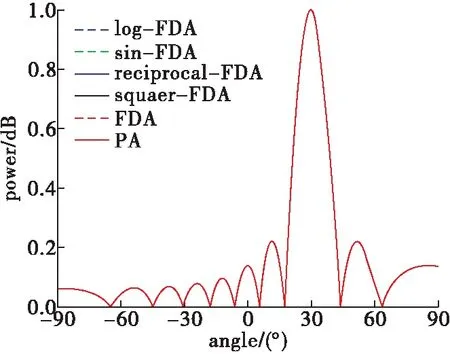


4.3 采用不同非线性频偏FDA的角度欺骗效果

4.4 Δf取值对角度欺骗效果的影响

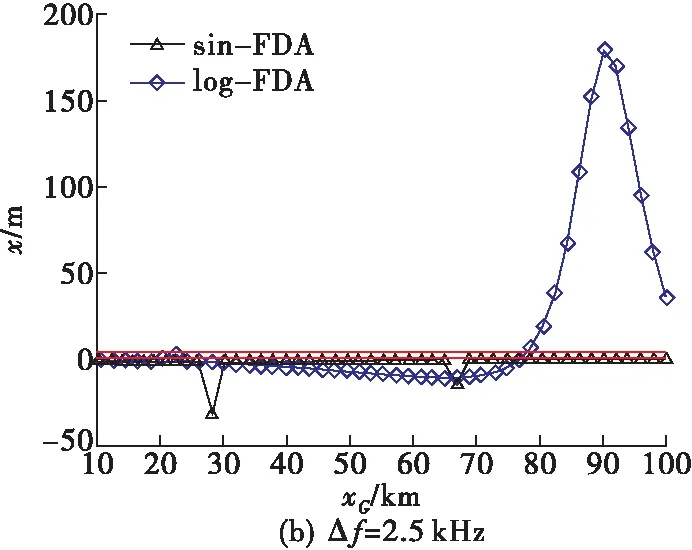
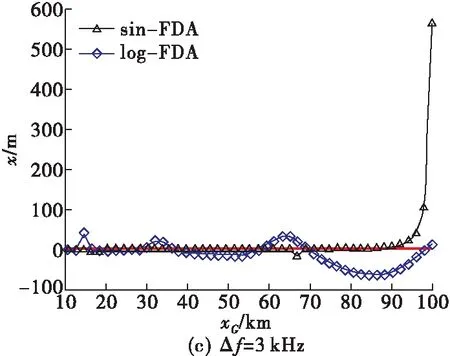

4.5 阵元间距对角度欺骗效果的影响


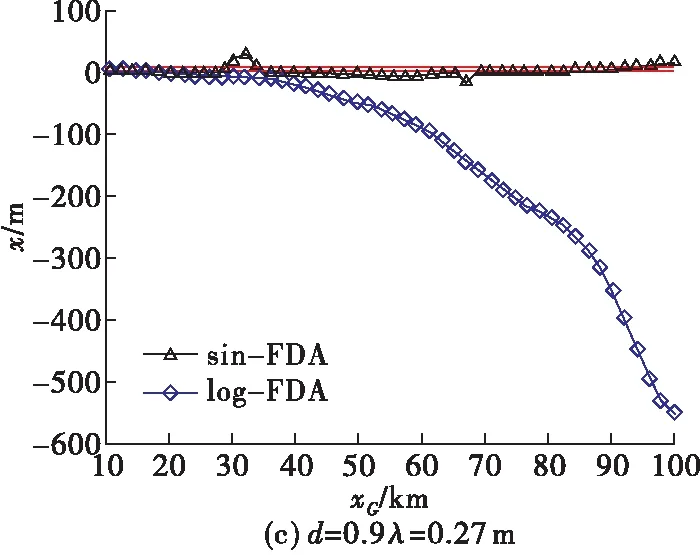
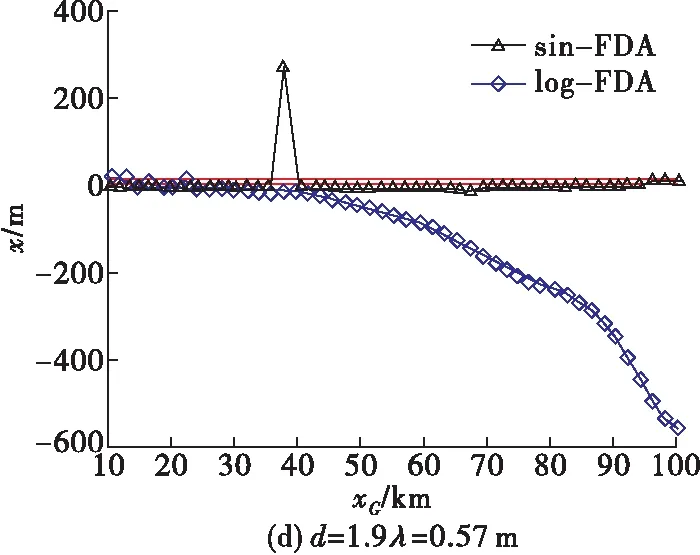
5 结语

