统一框架下在线核选择的竞争性分析*

廖 芸，张 骁，廖士中

天津大学 智能与计算学部，天津300350

1 引言

在线核选择（online kernel selection）旨在从候选核集中为在线核学习的每回合选择一个最优核，使得累积后悔最小且保证亚线性的累积后悔界。由于在线学习实时性和亚线性后悔界的要求，现有离线核选择的方法[1-2]和理论[3-4]均不适用于在线核选择。并且由于在线核选择需要同时进行模型的训练和选择，其实现方法和理论分析较离线核选择和一般的在线核学习更为复杂。因而近年来，在线核选择研究受到机器学习界的关注。

已有的在线核选择方法可分为专家建议框架（expert advice framework，EAF）和核学习（kernel learning）两类。在综述文献[5]中详细介绍了在线核选择的现有方法。在线核选择的专家建议框架方法是最经典的方法，适用于候选核集合是有限的情况。该类方法中，候选核集合中的每个核可看作是一个专家，通过选择一个核或核的分布来进行预测，每回合各个专家计算损失并更新下一回合选择核的策略。权重更新是基于专家建议框架的在线核选择中的关键步骤，有效的权重更新策略可以得到紧的后悔界。Yang 等[6]应用指数加权平均的方法来更新每回合各个核的权重，根据概率分布选出一个最优核，并通过在线到批处理的转换给出亚线性的期望后悔界。但该项工作面向的是离线核选择问题，且每次只更新所选择的核的权重。在线核选择也可以依据一个准则，并通过更新核参数来学习核。这种方法称为自适应核方法或核学习方法，该方法的效果依赖于原始设定的核参数。文献[7]通过应用梯度下降方法来更新核参数，从而得到核序列。文献[8]提出一种基于随机傅里叶特征的在线核选择方法，采用在线梯度下降来更新核参数。这两项工作均没有给出所提出方法的理论保证。文献[9]提出基于增量素描核对齐的在线核选择方法，对于强凸损失函数具有最优O(lnT)的后悔界，并且每回合具有常数的时间和空间复杂度。文献[10]提出基于局部后悔的在线核选择方法，具有亚线性后悔和关于回合数对数的时间复杂度。

不同于离线核选择的评价方法，在线核选择常采用后悔分析的评价方法，即分析并比较所选择的核的累计损失与对手环境下最优预测的累计损失之差。文献[11]系统综述了专家建议框架下在线凸优化算法的后悔分析。由于必须考虑对手的环境的设定，因而也可以采用博弈问题中的竞争性分析的评价方法。

竞争性分析旨在选取竞争比最小的方案。竞争比最早定义为在线算法的代价与最优离线算法的代价的最大比率[12]。该文献也详细综述了竞争性分析的问题和方法。亚线性的后悔表明在线决策者与离线最优决策差距不会太大，而常数倍的竞争比表明在线决策者与离线最优决策几乎可以一样好[13]。通过竞争比也可以得到预测者的后悔，此种后悔界说明对手越强预测者的后悔越小。竞争性分析可以从一个新的角度来评价在线核选择方法性能的优劣。已有的在线核选择理论关注在线核选择的静态后悔（static regret）分析，即竞争假设为单个假设的情形，而缺乏在竞争假设为假设序列的情形下对在线核选择竞争比的分析。

原始对偶方法是设计竞争性在线算法和证明竞争比的常用方法[14]，也被拓展到非线性规划用来处理无法自然松弛到线性规划的问题[15]。度量任务系统（metric task system，MTS）常应用竞争分析来评价性能，并且度量任务系统的竞争比可以不依赖于回合数[16]。度量任务系统虽与专家建议框架类似，但二者也有本质的不同：前者是已知代价再给预测（1-lookahead），后者是先预测再给出代价（0-lookahead）。这使得二者虽然过程相似但很难放在一个统一的框架中进行分析[17]。Buchbinder等基于专家建议框架和度量任务系统的相似性，将二者放在统一框架中进行分析。虽然二者理论度量不同，但采用原始对偶方法，既可以得到亚线性后悔，也可以得到较小的竞争比[18]。注意到没有在线学习算法可以同时得到亚线性的后悔和常数倍的竞争比[13]，该项统一框架工作非常值得关注。

已有在线核选择工作只采用了后悔分析的评价方法，既没有采用竞争性分析的评价方法，更没有尝试后悔分析与竞争性分析统一框架的工作。基于这一分析，提出期望在线核选择的概念，拓广了在线核选择的概念，并将期望在线核选择问题归约为专家建议框架问题。通过应用专家建议框架和度量任务系统的统一框架，同时给出期望在线核选择的亚线性后悔界和各类竞争比保证，将现有在线核选择研究推向新的阶段，为将来在线核选择研究开辟新的途径。

2 预备知识

定义所用到的符号并介绍相关概念。样本序列S={(x1,y1),(x2,y2),…,(xT,yT)}，其中(xt,yt)∈X×Y，X 为输入空间，Y 为输出空间。损失函数也称代价函数定义为c:Y×Y →ℝ。令核函数κ对应的再生核希尔伯特空间为Hκ，Hκ中假设f∈Hκ的范数记为||f||Hκ。记[T]={1,2,…,T}，并定义：

2.1 在线核选择

在线核选择问题旨在在线地选择一个核序列，使得所选择的假设（序列）能得到亚线性的后悔界。文献[6]提出一个在线核选择算法（online kernel selection，OKS）。应用指数加权预测的专家建议框架，在第t回合更新m个专家的第i个专家下一回合的权重wt,i，根据所选的核与调用的子算法得到对应的假设序列fi，i∈[m]，进而给出期望意义下的后悔界。

定理1[6]假设损失0≤ct,i≤L且||∇ℓ(∙,∙)||≤G，i∈[N]，t∈[T]，则OKS算法的后悔界为：

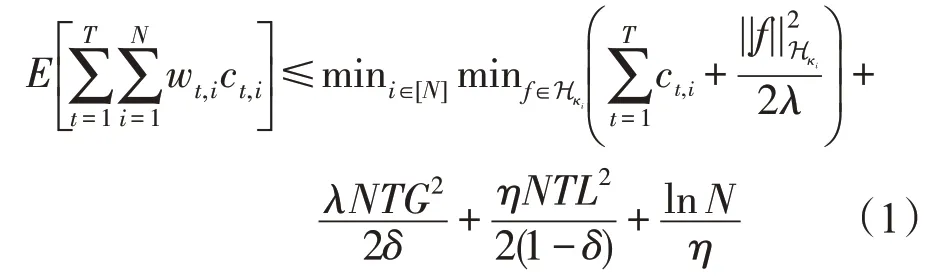
其中，ct,i表示第t回合选择第i个专家的损失，η为步长，λ为正则化参数，δ∈(0,1)为OKS 算法的平滑参数。

2.2 专家建议与度量任务系统的统一框架

专家建议框架（EAF）与度量任务系统（MTS）均是在线学习算法的数学模型。在线学习的专家建议框架与在线决策的度量任务系统既有相似又有区别，二者的统一框架中既可分别得到相应的理论保证，又可研究不同理论之间的关系。

文献[16]最早介绍度量任务系统模型，并给出形式化定义。度量任务系统作为研究竞争比的工具，设置从wt-1到wt会产生移动代价。与专家建议框架不同的是，根据观察到第t回合的代价，给出分布wt再进行预测。度量任务系统一般用竞争性分析作为理论保证，并与最优离线序列相比较。考虑α-不公平竞争比：

其中，α是与专家建议框架放在统一框架中讨论的参数，α≥1。当α≠1 时可弱化竞争，此时最优序列的移动代价要大于预测序列的移动代价。当α→∞，等同于在线环境下的最优分布，即与固定的最优分布相比较。

专家建议框架也可考虑更强的专家——漂移专家（drifting experts），即预测分布序列与最优分布序列对比，且最优分布序列满足如下约束：

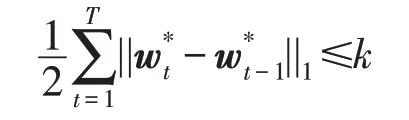
专家建议框架与度量任务系统的统一框架方法，主要思想是将在线度量任务系统与在线学习专家建议框架放入统一框架中，同步更新权重w，可同时得到亚线性后悔和较低的竞争比。记：

可按下式统一更新wt,i:

算法1 是专家建议框架与度量任务系统统一框架算法。

算法1EAF与MTS的统一框架

3 OKS算法后悔界的改进

先给出Hoeffding引理。

引理1令X为随机变量且满足a≤X≤b，则对任意的s∈ℝ，有：

应用引理1可改进定理1的后悔界如下。

定理2假设损失0≤ct,i≤L且||∇ℓ(∙,∙)||≤G，i∈[N],t∈[T]，则OKS算法的改进后悔界为：

其中，ct,i表示第t回合选择第i个专家的损失，η为步长，λ为正则化参数，δ∈(0,1)为OKS 算法的平滑参数。

证明记Wt=

应用引理1 可改进ln(Wt/Wt-1)的上界。只列关键步骤。由原文可得=I(it=i)，且。其中为第t回合第i个核的概率。对t∈[T]：

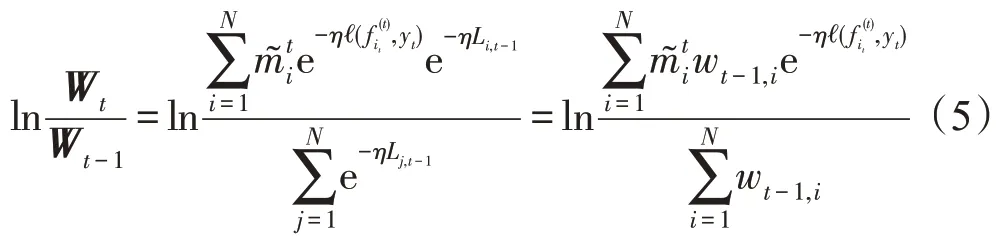
其中，Li,t-1为前t-1 个回合的累积损失。由引理1可得式（5）的上界：

其中，上述的不等式依赖于损失函数在第一项上的凸性。整理前T回合可得：

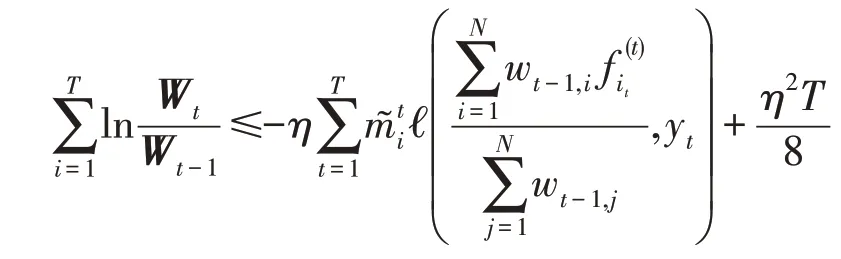
又由原定理证明可得：

联立上下界可得：

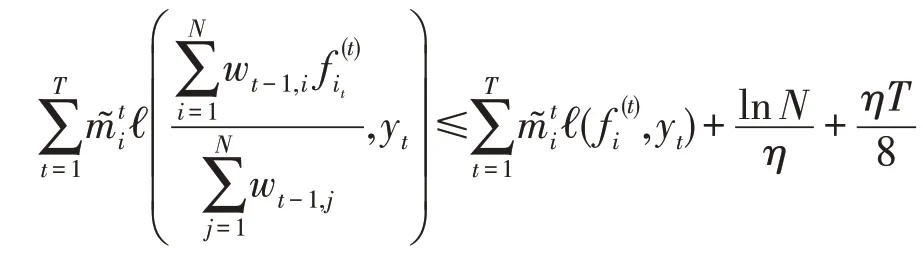
与式（1）相比较可得定理2给出的后悔界较定理1 给出的在常数项上改进4 倍。当回合数较小时，该后悔界会有显著的提升。但后悔界的改进不能直接得到更优的竞争比，有以下两点原因：（1）定理2中的后悔为静态后悔，即竞争策略为单个专家的预测，而竞争比中的竞争策略为专家序列的预测；（2）定理2中后悔界是由损失函数曲率参数和假设的范数表示的，而竞争比分析需要将后悔界表示为最优专家的累计损失。

4 统一框架下的在线核选择

在线核选择旨在每回合选择一个最优核以使累积后悔最小。可将在线核选择问题归约为专家建议框架问题，每个专家可以对应一个核，专家每回合的代价即为对应核的预测损失。

下面定义统一框架观点下在线核选择的几个相关概念。

定义1（期望在线核选择）给定候选核集合K={κ1,κ2,…,κN}，设||wt||1=1，wt,i≥0，t∈[T]，i∈[N]。期望在线核选择第t回合依据概率分布wt-1选择最优核κit∈K，其中it～wt-1，it∈[N]。

期望在线核选择中的wt的每个分量对应着候选核集合中不同核在每回合的重要程度。即wt-1,i为回合t专家i的权重。注意，若权重或概率分布为一确定分布（wt-1的分量只有一个分量为1，其余的都为0），则期望在线核选择退化为一般的在线核选择。

由于与不同类型的专家相比可引出不同的后悔和竞争性分析，故下面给出不同的后悔与竞争比的定义。

定义2（最优分布核后悔）期望在线核选择的最优分布核后悔为：

其中，ct为回合t每个核预测的代价，w*为候选核集合的最优分布。

上述定义中的最优分布为离线条件下得到的最优分布，此时可应用原始的竞争性分析方法。

下面给出针对漂移专家的期望在线核选择的后悔定义。

定义3（最优分布序列核后悔）期望在线核选择的最优分布序列核后悔为：

定义3中后悔的竞争策略为最优分布序列核，但最优分布序列核的性能不能评价该后悔上界的优劣，即后悔上界不可由最优分布序列核的累积损失表示。而竞争比可以建立最优分布序列核的累积损失和后悔上界的关系，因此考虑应用专家建议框架与度量任务系统的统一框架来进行期望在线核选择问题的理论分析，既可以得到一个较低的竞争比，又可以得到具有竞争意义的亚线性后悔界。为此给出期望在线核选择的竞争比定义。

定义4（最优分布核竞争比）对于期望在线核选择问题，T回合依据所选择分布wt-1得到的期望累计损失，与最优分布核的竞争比定义为最小的β，使得对任意的损失向量ct有：

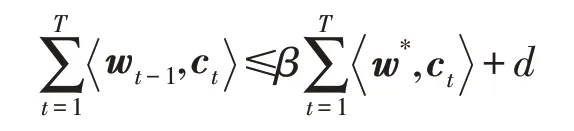
其中，d为独立于回合T的常数。

定义5（最优分布序列核竞争比）对于期望在线核选择问题，T回合依据所选择分布wt-1得到的期望累计损失，与最优分布序列核的竞争比定义为最小的β′，使得对任意的损失向量ct有：

其中，d为独立于回合T的常数。若竞争比为β，也可称为是β-竞争的。

5 理论结果

期望在线核选择问题归约为专家建议框架问题后，可应用专家建议框架与度量任务系统的统一框架来更新权重wt,i。在文献[18]工作的基础上，可得到如下定理。

定理3对于期望在线核选择问题，假设每个回合所选择核的预测代价为ct,i∈[0,1]，α(α≥1)为不公平竞争比中的参数（见式（2）），η为式（3）中更新w的参数。对任意的α≥1,η＞0，可分别得到如下的最优分布核竞争比和最优分布序列核竞争比。

（1）若α→∞，则统一框架所选择的核序列关于最优分布核是(1+η)-竞争的。

（2）若α=lnN/η，则统一框架所选择的核序列关于最优分布序列核为(1+3η)-竞争的。

定理3 的结论是在损失函数值域为[0，1]时得到的。当损失函数的值域扩展后，下面两个推论分别给出期望在线核选择在统一框架下，所选择的核序列的累计损失关于最优动态核序列累积损失和最优静态核累积损失的竞争比。

推论1当用所选择的核预测得到的损失函数ct,i∈[0,M]时，由定理3 的条件可得，统一框架所选择的核序列关于最优分布序列核是(1+3η)-竞争的。

证明考虑将损失函数映射到[0，1]后再带入到定理3。当损失函数ct,i∈[0,M]时，可将损失函数成比例缩减为：

带入定理3中再依据条件2可得：

由此可得，当损失函数值域为[0,M]时，仍可得到(1+3η)的竞争比。 □

由推论1 给出的后悔界（6）可知，每回合的最优核序列预测的累计损失越小，得到的后悔界越好，且当损失函数为[-M,0 ]时，可得到同样的竞争比。但当损失函数阈值为[-M,M] 时，做映射：

推论2当损失函数的值域为ct,i∈[0,M]时，依据定理3的条件可得，统一框架所选择的核序列关于最优分布核仍是(1+η)-竞争的。

证明同上。 □

对于有监督的在线核学习问题，期望在线核选择在第t回合选择最优核后，需要给出预测。假设第t回合的预测由在线核学习方法OKL(it)（应用核）产生的假设给出。令第t回合所选择的核在(xt,yt)上的损失为：

其中，ℓ(∙,∙)为损失函数。定义Regret(i)为OKL(i)的后悔界，i∈[N]，即：

其中

可得如下定理。

定理4对于期望在线核选择，假设每回合核选择的概率分布由式（3）产生。假设损失函数ℓ(∙,∙)是L-利普希茨连续的且ℓ(0,yt)=0,t∈[T]。令≤W，t∈[T]，α和η满足定理3中条件，则：

其中，Hκ为κ对应的再生核希尔伯特空间。

证明由损失函数的L-利普希茨连续性可得：

由于ℓ(0,yt)=0，i∈[T]，则：

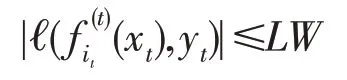
令ct为定义3中的代价，有：

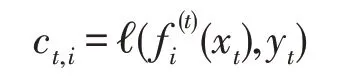
则由式（7）可得：

最终由推论2可得结论。 □

由定理4可得如下竞争比。

推论3对于有监督在线核学习问题，若损失函数满足定理4中的条件，且：

则统一框架所选择的核序列关于最优分布核是[1+(1+γ)η+γ]-竞争的。

上面的定理考虑的是最优核的后悔和竞争比，下面定理考虑最优分布核序列的后悔和竞争比。

定理5对于期望在线核选择，假设每回合核选择的概率分布由式（3）产生。定义OKL(i)关于的后悔界为Regret(i)，i∈[N]，若同样满足定理4 的条件，则对于最优分布核序列有：

证明依据定理4的证明和定理3结果可证。□

由上述定理可得最优分布核序列的竞争比。

推论4对于有监督在线核学习问题，若损失函数满足定理5中的条件，且：

则统一框架所选择的核序列关于最优分布核序列是[1+3(1+γ′)η+γ′]-竞争的。

统一框架针对在线核选择问题，可给出关于最优核及最优核序列的后悔界，对η取特殊值，可得到亚线性的后悔界。同时，此方法也可给出对于不同竞争假设的竞争比。

6 结束语

提出期望在线核选择的概念，将期望在线核选择问题归约为专家建议框架问题，并应用专家建议框架和度量任务系统的统一框架，分析了期望在线核选择的后悔界和竞争比。在统一框架下，不仅可全面拓展在线核选择的概念，涵盖期望意义和概念飘移情形下的在线核选择，又可同时研究这类在线核选择的后悔收敛性和竞争性，是在线核选择的一项崭新的研究工作。由于已有在线核选择问题是期望在线核选择问题的特例，这项工作更具一般性的理论价值，为在线核选择的未来研究工作开辟了新的途径。

应用统一框架不仅能给出较好的理论保证，也揭示出在对手环境下，对手的累计损失越小，在线核选择的竞争性越强。进一步工作拟研究新的专家权重更新方法以提高在线核选择的竞争性和收敛率。