双目视觉的立体匹配算法研究进展*

赵晨园，李文新，张庆熙

兰州空间技术物理研究所，兰州730000

1 前言

三维物体识别技术能提取目标物体的三维特征信息，进而对场景中一个或多个目标进行识别或分类，相较于传统二维图像识别更能准确全面地丰富物体的三维信息，从而进行更高维的特征提取以便处理更复杂的任务[1]，三维物体识别技术成为近年来计算机视觉领域的研究热点之一，被广泛应用于智能机器人、维修检测、无人驾驶、军事侦察等领域[2]。

双目立体视觉技术模拟人眼获取相同点产生的视差从而进行目标三维重建，获取三维图像[3]。与结构光传感器、TOF（time-of-flight）相机等获取深度图像方式相比，双目立体视觉技术对硬件、成本要求更低，所获取的深度图像更加密集、精确；与单目视觉深度估计相比，双目立体视觉技术计算复杂度更小，系统实时性更高。双目立体视觉技术更加适用于实际生产生活中的三维物体信息采集，有着巨大的发展空间和良好的应用前景[4]。

立体匹配是双目立体视觉技术中的核心算法，旨在通过寻找双目相机所获取的两张图像中的同名点从而构建视差图，一个良好的立体匹配算法直接决定三维重建的效果[5]，建立合适的立体匹配算法是提高基于双目立体视觉技术的三维物体识别效果的关键。

本文在通过分析总结现阶段主要的立体匹配算法的基础上，展望未来立体匹配算法的发展方向，旨在为今后相关领域人员开展立体匹配算法的研究提供思路与参考。

2 研究现状

立体匹配的目的是从两张图像中寻找同名点从而根据其视差计算出该点的深度信息[6]。Scharstein等[7]认为立体匹配算法通过匹配代价计算、代价聚合、视差计算/优化及视差校正四个过程实现。匹配代价是利用相似性函数计算左右图中像素点的代价，常用的相似性度量方法有绝对差值平方和（sum of absolute differences，SAD）、零均值绝对误差和（zero sum of absolute differences，ZSAD）、Census 变换（Census transform，CT）等；代价聚合通过邻接像素间的联系，用一定方法，对代价矩阵进行优化，以处理图像在弱、无纹理区域中的代价值无法准确配对的问题，降低异常点的影响，提高信噪比；视差计算/优化采用“赢家通吃”（Winner-takes-all，WTA）原则，在视差搜索范围内选择代价值最小的点作为对应匹配点，并确定该点视差；视差校正是对匹配好的视差图进行后处理，以解决遮挡点视差不准确、噪声点、误匹配点等问题，常用方法有左右一致性检查（left-right check）、中值滤波（median filter）、局部一致性约束（locally consistent）等。立体匹配算法根据算法特点可以分为局部、全局、半全局和基于深度学习的立体匹配算法。

2.1 局部立体匹配算法

局部立体匹配算法又称为基于滑动窗口的图像匹配方法，以待匹配像素的局部窗口内的像素为约束，通过在另一个视角中水平移动窗口，计算每个视差窗口内所有像素的匹配代价，利用赢家通吃原则，选择最小匹配代价值作为该点视差。局部立体匹配算法一般包含匹配代价计算、代价聚合和视差计算/优化三个步骤。

Kitagawa等[8]提出了基于高斯差分响应（response of the difference of Gaussian，DoG）的引导滤波匹配方法，使用SAD 和相邻像素梯度值的加权和来计算匹配代价，根据每个像素选择适当窗口，利用引导滤波对代价矩阵进行平滑聚合处理，时间效率高；Han等[9]改进了快速自适应窗口匹配算法，采用SAD计算颜色特征、梯度特征和纹理特征信息并分配不同权重作为匹配代价；Chai等[10]针对图像有大量噪声或视差不连续情况下存在虚假匹配的问题，将SAD 和Census 变换结合作为相似性度量函数进行立体匹配，建立了基于自适应窗口的引导滤波法进行代价聚合，结果表明该算法能提高匹配精度，对光畸变和边缘信息也有较好的鲁棒性；Hong 等[11]对基于加权引导图像滤波（weighted guided image filtering，WGIF）的局部立体匹配代价聚合方法进行改进，通过基于局部方差的自适应权重法重新构造代价滤波器，该算法效果优于其他滤波算法；Hamzah等[12]提出了iSM算法，在固定窗口下利用幅度差的梯度匹配和（sum of gradient matching，SG）计算匹配代价，利用自适应权重的迭代引导滤波（adapive support weight with iterative guided filter，ASW-iGF）算法进行代价聚合，采用WTA方法确定最终视差并用联合加权导频滤波器（joint weighted guided filter，JWGF）对视差进行后处理以降低噪声；Oussama等[13]利用改进的Census变换计算匹配代价，提出了基于交叉聚合的自适应代价聚合方法（cross-based aggregation method），算法能改善弱纹理区域误匹配率高的问题。

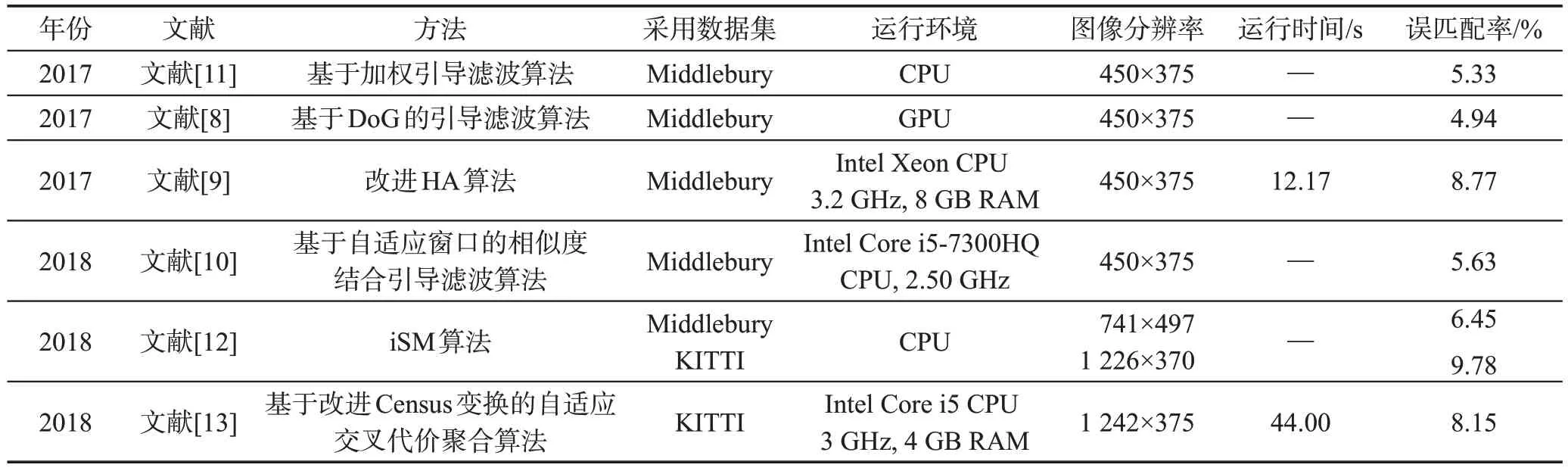
Table 1 Effects of different local stereo matching algorithms表1 不同局部立体匹配算法效果

表1 是不同局部立体匹配算法的效果，表1 中，Middlebury为室内有遮挡物体图像数据集，KITTI 为室外道路场景数据集，两数据集均采用误匹配率作为算法评价标准，误匹配率计算公式如下：

式中，err为误匹配率，N为图像总像素个数，dC(x,y)是由算法得到的视差值，dT(x,y)为Ground truth视差值，δd为误差阈值，大于该阈值表示该点没有匹配成功，取值在0.5～4.0 之间。使用Middlebury 数据集能分别计算视差不连续区域disc、非遮挡区域nonocc和全区域all 的误匹配率；使用KITTI 数据集能计算背景区域bg 的误匹配率、前景区域fg 的误匹配率和全区域all误匹配率。本文表中误匹配率为图像的全区域all平均误匹配率。

局部立体匹配算法通过滑动窗口，利用像素周围的局部信息对处于同一极线约束的所有点计算匹配代价，从而找出同名点，相对于全局立体匹配算法，该匹配算法具有计算复杂度低，时间效率高的优点，但由于未充分考虑图像的全局信息而导致其很难区分无、弱纹理区域的不同像素点，且对深度不连续区域存在鲁棒性差的缺点。因此，研究者通过组合不同相似性度量方法及选用不同代价聚合方法以提高匹配精度。由表1可知，局部算法的平均误匹配率为7.01%；Kitagawa 等[8]提出的算法在Middlebury数据集中误匹配率为4.94%，匹配效果最好。该算法改善了传统局部算法选择的匹配窗口和聚合滤波窗口对不同区域适应性差的缺点，利用自适应窗口的引导滤波法进行代价聚合，为边缘区域像素点选择较小尺寸窗口，为无纹理区域选择较大尺寸窗口，相比于传统引导滤波方法，提高了匹配精度。

2.2 全局立体匹配算法

全局立体匹配算法又称为全局能量函数最小法，该方法将局部匹配代价和平滑约束条件组合在一起构成全局代价函数，通过不断迭代优化分配的视差值，直到全局能量函数最小化。全局立体匹配能量函数定义如式（2）所示。

式中，E(D)为全局能量函数；E(data)(D)为数据约束项，用于判断像素点之间的相似性；E(smooth)(D)为相邻点的平滑约束项，用于判断相邻点之间的连续性；λ为参数因子，用于数据项和平滑项的平衡。全局立体匹配算法通常包括匹配代价计算、视差计算/优化与视差校正三个步骤。经典的全局立体匹配算法有动态规划[14]、图割[15]和置信传播法[16]。

Hallek等[17]利用零均值绝对差和（ZSAD）计算匹配代价，并用动态规划法进行优化，建立了具有实时性的立体匹配系统；Cheng等[18]提出了粗加精的匹配思想，该方法为在建立新的全局边缘约束（global edge constraint，GEC）基础上，利用局部算法估计最优支持窗口，建立初始视差图，并根据匹配结果构造数据项，将GEC 作为平滑约束纳入全局能量函数中并利用图割法进行最小化处理得到精确视差图；San等[19]为了实现对无纹理区域更好的视差估计，将爬山算法（hill-climbing）应用于图像分割，利用SIFT（scaleinvariant feature transform）和SAD融合的算法计算代价值，利用图割法对能量函数进行最小化处理获得最终视差；Ma 等[20]将绝对强度差（absolute intensity differences，AD）、绝对梯度差（absolute gradient differences，GAD）和基于梯度Census 变换（gradient-based Census transform，GCT）相似性度量方法组合成鲁棒性强的代价组合指数函数，计算匹配代价，采用互一致性检验准则和随机样本一致性算法组成的“MCRANSAC”的视差优化方法滤除异常值，用置信传播法优化能量函数得到较为精确的视差图；Wang 等[21]将SAD 和Census 变换组合形成匹配代价，将其转化为能量函数中的数据项并利用置信传播法进行迭代推理获取视差图，利用中值滤波和交叉检查滤波进行后处理优化，所选用的数据项在无纹理区域具有鲁棒性；Lee等[22]将Census变换和梯度图像匹配组合计算像素的初始代价，提出了一种新的自适应权重重启随机游走（adapt random walk with restart，AWR）视差优化算法，该算法复杂度较低；Tan等[23]利用像素点在0°、45°、90°和135°四个方向上的值拟合多项式函数，利用多项式函数计算该点视差值并作为数据项，利用置信传播法进行视差优化，结果表明该算法在高度倾斜的曲面上具有良好的匹配性能，虽然增加了算法的复杂度，但算法具有高并行性，便于GPU加速；Shahbazi等[24]用内禀曲线（intrinsic curves）的几何特征形成基于方向的稀疏视差假设值并将其作为遮挡项，非参数Census变换作为数据项，集成为全局能量函数，减少了由于图像像素遮挡而产生的误差，匹配率提升了2%。

全局立体匹配算法通常无代价聚合步骤，是通过不断迭代，利用全局能量函数为每一个像素点进行视差分配，使得能量函数最小，全局算法获得的视差值更接近真实视差值。误匹配率的定义不是考察像素点对是否正确匹配，而是计算该点视差与真实视差的差值是否小于误差阈值，全局算法平滑了相邻像素点之间的视差值，故其对视差连续及无、弱纹理区域匹配效果较好，匹配精度高，但不断的迭代增加了算法复杂度。为了提高识别精度和运行效率，研究者们通常对传统全局算法进行优化以提高识别精度或更换加速平台以提高时间效率。从表2 可以看出，全局算法的平均误匹配率为5.75%，比局部算法低1.26 个百分点，其中以Ma 等[20]的算法匹配效果最好，在Middlebury数据集中误匹配率为4.21%。该算法在改进能量函数并将置信传播法作用于区域而非像素以减小算法复杂度的基础上，结合局部自适应窗口的多相似度融合方法和全局置信传播方法，有效降低了误匹配率，但匹配代价的计算较为复杂，导致运行时间较长。利用局部和全局思想结合的方法取得最优视差图，给研究者提供了一个很好的思路。

2.3 半全局立体匹配算法

半全局立体匹配算法（semi-global matching，SGM）是近年来的研究热点之一，2005 年由Hirschmüller[25]提出，与全局匹配方法不同，该算法将二维图像的优化问题转化为多条路径的一维优化问题，计算像素点的匹配代价，聚合来自8 个或16 个方向的路径代价，并利用WTA 方法计算视差。半全局立体匹配算法一般步骤包括匹配代价、代价聚合、视差计算/优化和视差校正。半全局与全局立体匹配算法均采用最优化能量函数的思想，通过最小化全局能量函数估计最佳视差值，半全局方法采用的能量函数如下：

Table 2 Effects of different global stereo matching algorithms表2 不同全局立体匹配算法效果

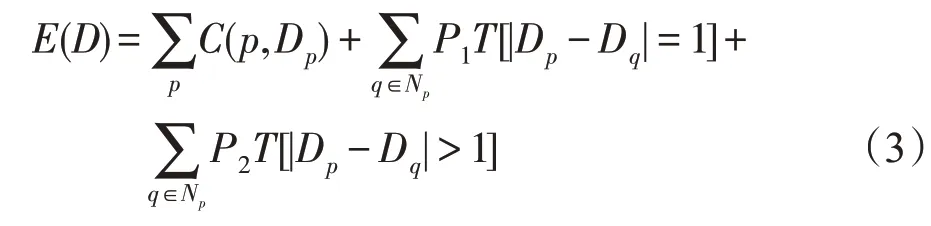
式中，E(D)为半全局能量函数；p是目标像素点，q为像素p邻域中的一点，Dp和Dq分别为两点视差，C(p,Dp)为视差图D下所有像素点的匹配代价，P1是平滑约束惩罚因子，是对相邻像素视差等于1(|Dp-Dq|=1)时添加的惩罚因子；P2是边缘约束惩罚因子，是对相邻像素视差大于1(|Dp-Dq|＞1)时添加的惩罚因子，P2＞＞P1。

Banz 等[26]根据数据流流入行缓存的方式，利用秩变换进行匹配代价计算，将8路代价聚合改为4路并行代价聚合，实现了对FPGA（field programmable gate array）的算法优化。在最大视差为128像素和时钟频率39 MHz 情况下吞吐量为37 frame/s（640×480像素），算法具有实时性；Li等[27]利用Census变换计算匹配代价，采用图像金字塔对每一层进行8 方向SGM处理，建立了一个由粗到精并行立体匹配算法，减少了匹配时间；Juarez等[28]利用GPU 对4路径实时SGM 算法进行并行加速，将其应用于实时辅助驾驶系统，吞吐量为42 frame/s（640×480像素）；Wang等[29]针对现有立体匹配算法对弱纹理和视差不连续区域匹配精度低的问题，提出了匹配代价组合的SGM 方法，用自适应权重SAD 和GAD 的组合计算匹配代价，用8路径的半全局方法进行代价聚合；Chai等[30]提出了基于最小生成树（minimum spanning tree，MST）的新型SGM 方法，该算法根据4 个规划路径上的像素点计算匹配像素点的代价值，根据叶节点到根节点和根节点到叶节点两个步骤之和计算代价聚合。视差图像在图像边缘产生的误匹配点比经典SGM算法少；Li等[31]利用灰度和梯度的融合信息计算匹配代价，利用互信息进行匹配代价的相似性度量，采用5条自适应加权路径进行代价聚合，匹配精度提高了1.74%，采用尖峰滤波器（spike filter，SPF）和左右一致性检查进行视差校正，系统吞吐量为197 frame/s（1 280×960 像素）；Rahnama 等[32]针对传统算法在FPGA上实现会产生条纹效应的问题，利用Census变换计算代价，改进能量函数并将8路径代价聚合变为4 个相邻像素点的聚合，利用中值滤波法降低噪声，系统吞吐量为71 frame/s（1 242×375像素），系统功耗低，适用于低功耗的实时性系统。

由式（3）的算法能量函数可知，SGM算法实质上是全局算法的一种改进，综合了全局和局部算法的优点，利用多条路径下的一维代价聚合问题来代替全局能量函数的最优问题，即将全局算法中的视差计算步骤简化并作为代价聚合步骤。算法在保留了匹配精度的同时，减小了计算复杂度，但匹配效果依赖于选取路径数目，算法对无、弱纹理区域的匹配效果与路径聚合数目成正比。另外，SGM 在利用硬件加速时往往受限于运算机制，例如算法在FPGA上实现时，为保证算法实时性而舍弃像素下半部分未读取路径的代价聚合，造成条纹效应，影响匹配精度。因此，如何在减少聚合路径前提下，通过优化算法保证匹配精度是SGM 在硬件平台上实现的难点之一，目前主要通过改变不同路径及添加权重以提高算法精度。在算法速度方面，研究者们利用GPU和FPGA并行计算的特点，通过增大空间复杂度、减小时间复杂度以实现实时性。由表3可知，半全局算法平均误匹配率为7.09%，比全局算法高1.34 个百分点，但利用FPGA或GPU硬件加速平台的算法运行时间均在1 s以下，可用于实时性要求高的系统中。

Table 3 Effects of different semi-global stereo matching algorithms表3 不同半全局立体匹配算法效果

2.4 基于深度学习立体匹配算法

基于深度学习的立体匹配算法是近年来兴起的一种算法，可分为两类，分别是深度学习与传统算法相结合的立体匹配算法和端到端的深度学习立体匹配算法。深度学习与传统算法相结合的算法是将深度学习算法应用于传统匹配算法的步骤中，让计算机自动学习匹配代价、代价聚合等，减少了人为设计造成的误差。基于端到端的方法直接以左右两张图像为输入，视差图作为输出，利用深度算法学习原始数据到期望输出的映射。

在深度学习与传统算法相结合的立体匹配算法方面，Zbontar 和LeCun[33]首次以成对小图像块、标注图像（ground truth）为输入，匹配代价为输出，训练有监督学习的匹配代价卷积神经网络（matching cost convolutional neural network，MC-CNN），使用交叉代价聚合方法聚合匹配代价，通过SGM 方法实现平滑性约束，对遮挡区域进行左右一致性检验，通过中值滤波器和双边滤波获得最终的视差图；Chen 等[34]针对现有监督学习方法普遍存在过拟合问题，提出在MC-CNN 基础上通过卷积层中选择2×2 小尺寸卷积核并在决策层中利用dropout正则化方法的图像块匹配代价算法，结合SGM 方法进行视差优化并采用左右一致性检验等多种方法进行视差校正，算法具有更好的泛化能力；Yan等[35]提出了对MC-CNN得到的视差图进行优化的后处理方法，该方法用马尔科夫推理估计像素点和遮挡区域的平均视差以进行全局优化，用贝叶斯推理进行视差优化达到局部优化，算法效率高；Williem 等[36]提出一种基于深度卷积网络的自我引导的代价聚合方法，并应用于局部立体匹配。该方法的深度学习网络由动态权值和下降滤波两个子网络组成，网络中结合特征重建损失和像素均方损失函数以保持边缘特性；Lee等[37]针对精确立体匹配算法占用内存多的问题，提出具有高效且鲁棒的置信度参数SGM（confidence-based parametric SGM，cbpSGM）算法，该算法对8路径SGM算法进行改进，组合高斯混合模型（Gaussian mixture model，GMM）参数聚合与eSGM[38]中两步聚合策略进行代价聚合，引入随机森林框架作为代价优化方法，算法内存低，为传统SGM的3%以下。

在端到端的深度学习立体匹配算法方面，Mayer等[39]于2016年首次将端到端神经网络模型应用于立体匹配领域，建立了大规模合成数据集并训练端到端卷积神经网络DispNet，该算法利用自动编码-解码结构，直接输出视差图，无后处理步骤，精度高；Pang等[40]提出了一种新的二级级联结构CNN（convolutional neural network），第一级通过增加额外的上卷积模块对DispNet改进使视差图具有更多细节；第二级用串联残差学习网络（cascade residual learning，CRL）进行视差细化，利用多个尺度上产生的残差校正视差；Kang 等[41]针对算法在深度不连续和低纹理区域方面匹配效果不佳的问题，提出改进DispNet神经网络的学习算法，该算法用扩展卷积建立上下文金字塔特征提取模块，构建基于图像块的匹配代价计算方法，将视差梯度信息引入损失函数进行后处理以保持局部细节；Brandao等[42]在Siamese神经网络中使用反卷积提取目标像素周围特征并进行特征点匹配，优化特征聚合算法，将学习网络变为浅层架构，降低了算法复杂度；Nguyen等[43]为解决弱纹理区域的误匹配问题，提出广域上下文学习网络和带空间扩散模块的堆叠式编码-解码二维CNN，该网络利用扩展卷积层和空间金字塔池化层提取全局上下文信息，利用提取的信息构成匹配代价，对匹配代价进行上下文代价聚合，算法无需后处理。

深度学习算法在立体匹配算法中的应用取得了巨大突破，其算法精度普遍超过传统立体匹配算法。针对传统方法在算法和参数选择上依赖经验、与实际问题适应性差、效率低下的问题，深度学习与传统方法相结合的匹配方法通过在传统算法中嵌套一个或多个深度学习算法，利用神经网络自主学习匹配代价或代价聚合以达到比传统方法更好的效果，通过直接学习原始图像，使得模型具有更好的泛化能力，算法难点在于算法与算法之间的契合问题；基于端到端的神经网络利用单个神经网络解决多步骤问题，规避了多步骤所产生的误差累积，避免了模块与模块间相互影响和人工设计的浅层表达产生的误差，将立体匹配完全转化为定位回归问题，充分利用卷积神经网络的特征提取能力和模型表达能力，自发地从图像数据中学习约束表达，是未来的发展趋势之一。但基于端到端的神经网络算法往往需要大量的数据集进行训练以增强模型泛化能力，且算法多为卷积计算，因此相比于非端到端的神经网络，端到端神经网络在有足够充足的训练集情况下具有更好的收敛性和泛化能力，但也会提高算法的时间复杂度。

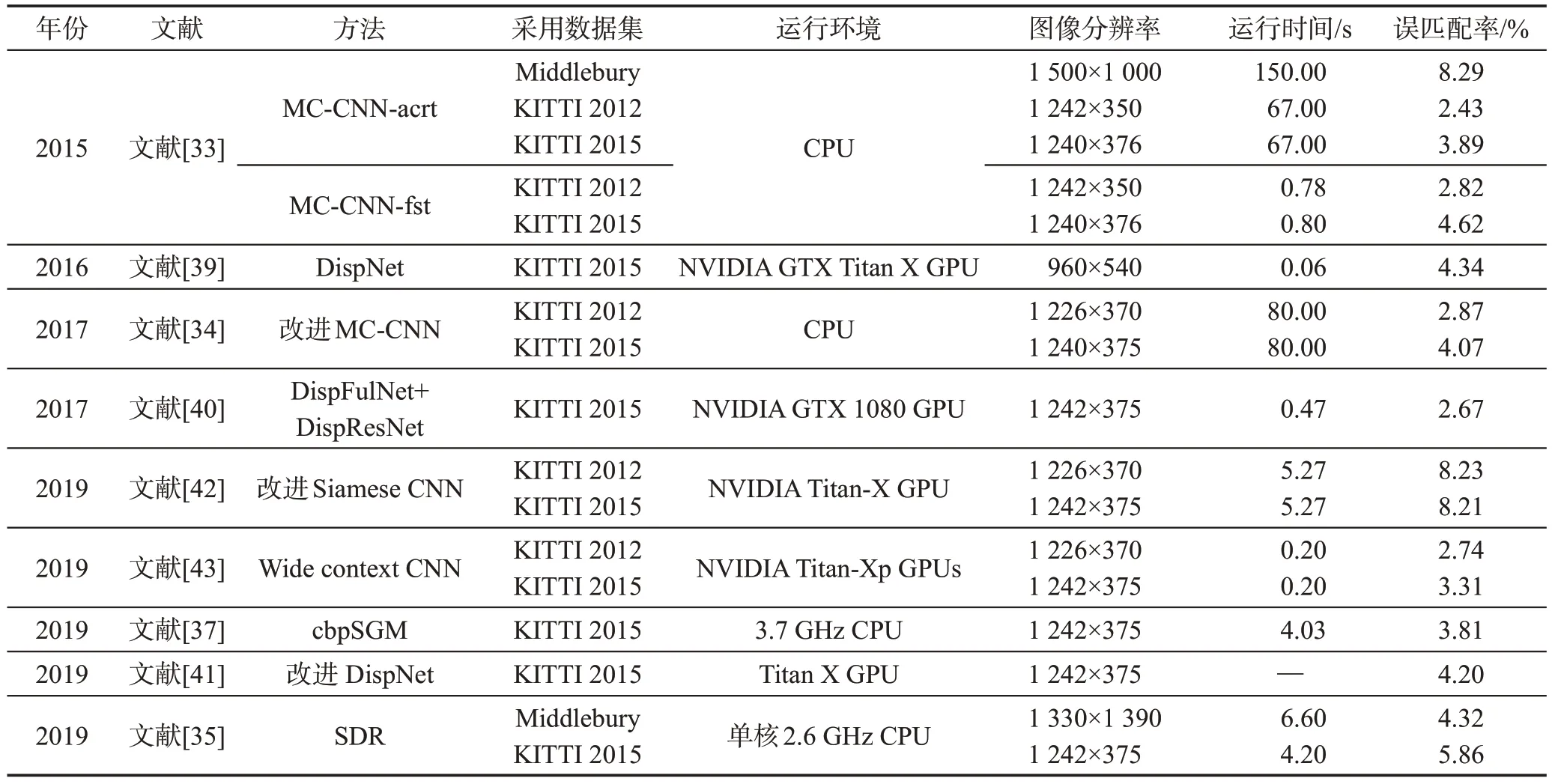
Table 4 Effects of different stereo matching algorithms based on deep learning表4 不同基于深度学习的立体匹配算法效果

从表4可以看出，基于深度学习的算法平均误匹配率为4.50%，优于局部、全局、半全局算法；深度学习与传统方法结合的算法均利用CPU 进行实现，而端到端算法均通过GPU 并行加速实现，端到端的深度学习算法比深度学习与传统方法结合的算法时间效率平均提高66倍，且匹配精度没有明显下降。

3 展望

近年来，双目立体视觉技术在工业上表现出巨大的应用前景和发展潜力，成为研究者们探索的热点之一，在立体匹配方面不断涌现出新的算法，推动匹配算法向高精度、实时性方向发展。

（1）现有研究的立体匹配算法大都依靠Middlebury、KITTI等数据集对算法进行学习、训练和验证，没有利用实际生产生活中的图像，实际拍摄的图像往往存在着无、弱纹理及反光、遮挡等区域。针对该问题，虽然Ran和Xue等[44-45]进行了有益的探讨，改善了弱纹理区域误匹配问题，但提高了算法复杂度。未来提出对弱匹配区域具有鲁棒性及实时性强的立体匹配算法仍具有重要意义。

（2）现有的研究普遍关注提升算法的匹配精度，但利用Middlebury 数据集建立的匹配算法中精度前十名的算法运行时间均超过120 s，不满足计算实时密集型任务的要求[35]。在传统立体匹配算法方面，可通过多种匹配代价算法融合，同时适当减小匹配窗口或聚合路径，在保证算法准确度情况下，减小算法复杂度；在深度学习算法方面，可通过优化卷积核，将深度学习算法与传统算法进行融合以减小对大量数据集的依赖，同时也要防止算法过拟合。此外，FPGA 和GPU 具有流水线并行计算的能力和可对大规模数据流进行并行处理的优点，未来利用FPGA和GPU硬件加速平台实现算法并对其进行优化将是解决图像实时匹配问题的一种思路。

（3）当前算法处理的图像分辨率普遍较低，许多算法利用1/4精度或半精度图像进行算法验证，无法达到应用要求。随着计算机视觉技术的发展，高分辨率图像的立体匹配算法将成为一种发展趋势。下一步，在保证实时性前提下，提出高精度、高分辨率的立体匹配算法是未来发展方向。

（4）现有研究表明，深度学习算法对立体匹配的精度较高，成为近年来的热门研究方向之一，也是未来的发展方向，其中的深度学习与传统立体匹配算法用来优化立体匹配中匹配代价、代价聚合等，但模型之间存在着难以融合的缺点。下一步，将深度学习算法与传统算法并行处理，结合使用，解决算法与算法之间的调优问题以进一步提升模型的泛化能力；端到端的深度学习方法匹配精度高，一个神经网络就可完成多个匹配步骤，将被越来越多地应用于立体匹配领域。因此，如何利用像素上下文信息，充分发挥卷积神经网络的作用，并减小内存消耗，是研究者需要考虑的问题。

4 结束语

立体匹配是双目立体视觉技术中实现三维重建的关键，对双目立体视觉技术的应用及发展有着决定性的意义。下一步立体匹配算法的研究重点为解决在无、弱纹理区域匹配精度不佳的问题，开发基于深度学习的高精度立体匹配算法和具有高实时性、可实际用于生产需要的立体匹配算法。本文对提高双目立体视觉技术中立体匹配的水平具有参考价值。