鲁棒概率矩阵三分解*

史加荣，陈姣姣

1.省部共建西部绿色建筑国家重点实验室/西安建筑科技大学，西安710055

2.西安建筑科技大学 理学院，西安710055

1 引言

在人工智能与大数据时代，推荐系统、图像处理和运动结构重建等诸多应用领域的科学研究都是在处理数据矩阵。这些矩阵不仅规模庞大，还可能伴随数据缺失、被污染和存在异常值等情况。解决上述问题的常用方法是低秩分解，例如主成分分析（principal component analysis，PCA）[1]、奇异值分解（singular value decomposition，SVD）[2]和非负矩阵分解（non-negative matrix factorization，NMF）[3]等。传统的矩阵分解方法一般采用l2范数来度量逼近误差，但它对数据中的异常值具有很高的敏感性。

为了克服PCA 对稀疏噪声的敏感性，文献[4]提出了鲁棒主成分分析（robust PCA，RPCA），该模型假设噪声是稀疏的，通过求解非凸的l1范数最优化问题来获得低秩逼近。随后，一些学者研究了RPCA的凸优化模型[5-8]，并提出了求解模型的主成分追踪方法（principal component pursuit，PCP）[9]。在鲁棒主成分分析等鲁棒矩阵分解模型中，仍假设低秩矩阵的元素是确定性的，这可能会导致过拟合现象，也不利于研究数据的生成方式。为了避免上述弊端，概率低秩矩阵分解模型假设低秩成分和噪声矩阵均服从某种随机分布[10]。对于概率低秩矩阵分解模型，可以通过期望最大化（expectation maximization，EM）算法、Gibbs 采样或变分贝叶斯来求解模型参数[11-20]。为了增强模型的鲁棒性，可假设噪声矩阵的元素服从拉普拉斯分布[21-22]。

概率矩阵分解（probabilistic matrix factorization，PMF）[23]和鲁棒概率矩阵分解（robust PMF，RPMF）[24]是两种重要的概率分解模型。在PMF 中，均假设低秩矩阵和噪声矩阵服从高斯分布。RPMF 基于马尔科夫链蒙特卡洛（Markov chain Monte Carlo，MCMC）技术，能达到比PMF 更高的预测精度。但从本质上讲，这两种方法都等价于l2范数优化模型，它们对数据的异常值依然比较敏感。而鲁棒贝叶斯矩阵分解（robust Bayesian matrix factorization，RBMF）[25]和贝叶斯鲁棒矩阵分解（Bayesian robust matrix factorization，BRMF）[26]在非确定性框架下解决模型的鲁棒性问题。RBMF 将贝叶斯概率矩阵分解中的高斯噪声替换成高斯混合噪声，并且采用重尾的学生t分布作为低秩矩阵的先验分布。为了减轻异常值对模型结果的不利影响，BRMF综合运用了高斯先验和拉普拉斯噪声，比其他算法具有更好的鲁棒性。前述概率低秩矩阵分解模型均将数据矩阵分解为两个低秩矩阵的乘积，使得模型缺乏灵活性和实用性。最近，文献[27]提出的矩阵三分解模型（tri-decomposition model，Tri-Decom）将数据矩阵分解为低秩、稀疏噪声和稠密噪声三个分量矩阵之和，但该模型没有考虑低秩矩阵的分解，也没有使用概率模型。为此，本文建立了鲁棒概率矩阵三分解模型（robust probabilistic matrix tri-factorization，RPMTF），并提出了求解该模型的条件EM算法。

2 预备知识

定义1（矩阵范数）矩阵A=(aij)m×n∈ℜm×n的l1范数为，Frobenius范数为。

定义2（Kronecker 积）设A=(aij)m×n∈ℜm×n，B=(bst)p×q∈ℜp×q，称如下的分块矩阵

为A与B的Kronecker积。

定义3（矩阵向量化）设A=(aij)m×n∈ℜm×n，称mn维列向量

vec(A)=(a11,a21,…,am1,a12,a22,…,am2,…,a1n,a2n,…,amn)T为矩阵A的逐列向量化。

定理1（奇异值分解）对于秩为r的矩阵A∈ℜm×n，它的奇异值分解为：

其中，U∈ℜm×m和V∈ℜn×n均为正交矩阵，对角矩阵Σr=diag(σ1,σ2,…,σr)的对角线元素满足σ1≥σ2≥…σr＞0。

本文用到的概率分布如表1所示，其中广义逆高斯分布中的Kp(·)表示二阶修正的贝塞尔函数，c=，d=b/a。

3 鲁棒概率矩阵三分解

3.1 模型建立

假设数据矩阵D=(dij)m×n∈ℜm×n具有近似低秩结构，通常使用矩阵分解方法进行维数约减和噪声移除。在加性高斯噪声腐蚀下，可使用奇异值分解来得到D的最优秩k逼近矩阵L，即：

其中，k＜min{m,n}，S∈ℜk×k为对角矩阵，U∈ℜm×k与V∈ℜn×k满足UTU=VTV=Ik，Ik为k阶单位矩阵。

将矩阵U和V按列分块，即U=(u·1,u·2,…,u·k)，V=(v·1,v·2,…,v·k)，易知：

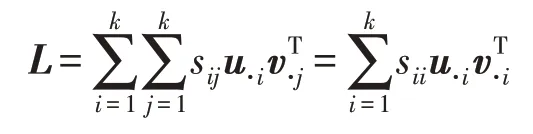
为了更加灵活地获得矩阵的低秩逼近，本文考虑将数据矩阵D的低秩成分重新分解为三个矩阵的乘积，即有如下公式：

与式（1）相比，上式中E∈ℜm×n是噪声矩阵，且不要求矩阵S为对角方阵。下面建立鲁棒概率矩阵三分解模型。

假设矩阵U、S、V和E均是连续型随机变量，对应的概率密度函数分别记为p(U)、p(S)、p(V)和p(E)。根据极大后验估计、期望最大化或变分贝叶斯等方法可求得D的低秩近似。考虑数据矩阵D受到大的稀疏噪声的腐蚀，为增强矩阵分解模型的鲁棒性，可假设噪声矩阵E服从拉普拉斯分布。本文给出一类简单的概率矩阵三分解模型：

矩阵集合{U,S,V}的后验概率密度为：

对上式取对数，得：

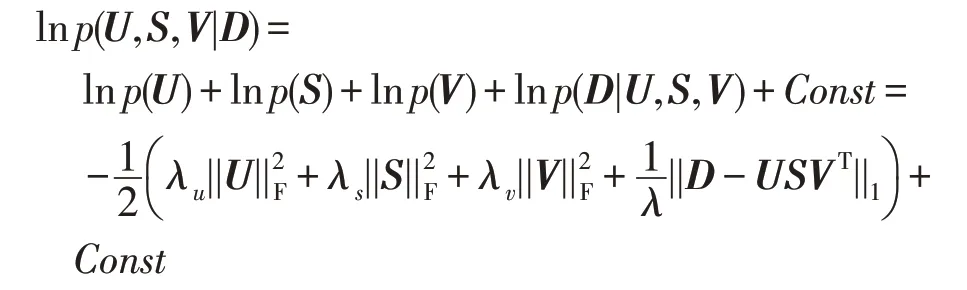
其中，Const是与U、S、V无关的常数项。根据极大后验估计法，最优的低秩逼近矩阵可通过求解下列最优化问题来获得：

Table 1 Several commonly-used probability distributions表1 几种常用的概率分布

最优化问题（5）的目标函数是非光滑的，故可使用分层模型来处理拉普拉斯分布[28]。因为：

故建立针对拉普拉斯分布的分层模型：

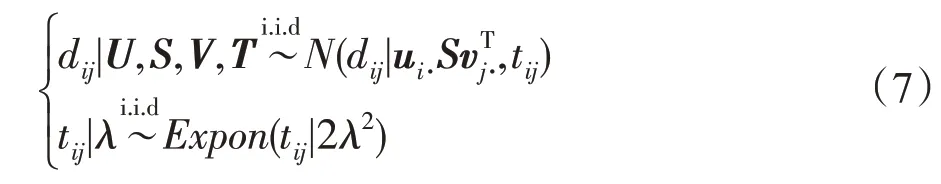
随机变量矩阵T=(tij)m×n为隐变量，{D,U,S,V,T}为完整数据。结合式（3）和式（7），使用条件期望最大化方法估计D的最优低秩逼近。

3.2 条件EM算法

记θ={U,S,V}为待估参数矩阵集合。采用条件期望最大化（conditional expectation maximization，CEM）[29]方法求解最优的参数θ。具体而言，在算法迭代过程中先求隐变量tij的倒数的期望，再使用最大化模型更新U、S和V。令上次迭代过程得到的参数为，据此得到参数的更新公式。

（1）更新V

①E步

根据贝叶斯规则，V的后验分布可表示为：

对上式取对数，得:

其中，Const是不依赖于V的常数。

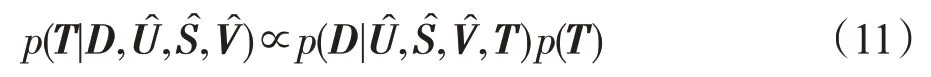
结合式（7），得到tij的条件概率分布密度：

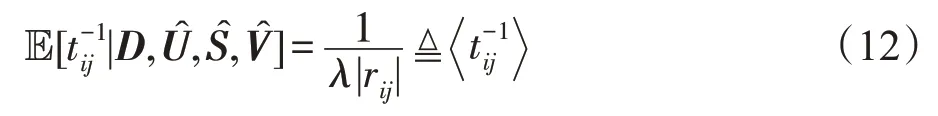
②M步

通过最大化Q函数来更新矩阵V。记：

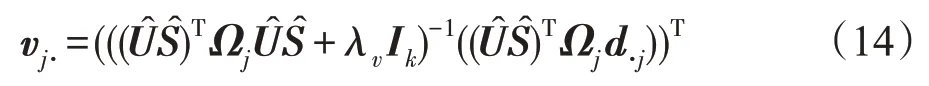
（2）更新U

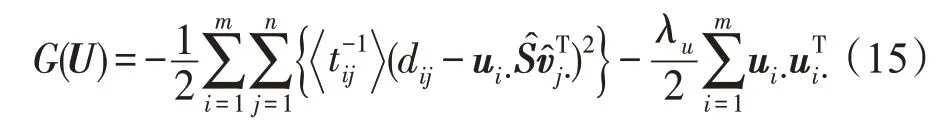
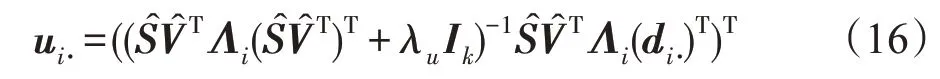
（3）更新S

为了最大化H(S)，将矩阵S逐列向量化，得到k2维列向量vec(S)。于是：

再将vec(S)矩阵化，得到S。

下面列出求解概率矩阵三分解的条件EM算法。

算法1求解RPMTF的条件EM算法

在上述算法中，可设置终止条件为达到最大迭代次数或：

其中，ε为一个比较小的正常数，{Uiter,Siter,Viter}表示第iter次迭代的结果。

3.3 计算复杂度

下面讨论算法1 在一次迭代过程中的计算复杂度。不失一般性，假设m≤n。E 步的更新过程主要涉及残差矩阵R的计算，因为USVT的计算复杂度为O(mnk+mk2)，所以E步计算复杂度均为O(mnk+mk2)。对于U、V和S更新过程的M步，对应的计算复杂度分 别为O(mk2+k3)、O(nk2+k3) 和O(mnk4+k6) 。因此，一次迭代中总计算复杂度为O(mnk4+k6)。可以看出：算法1 的计算复杂度主要集中在S的更新上。在实际应用中，k的取值不宜太大。当k的取值存在上界时，算法1 在一次迭代过程中的计算复杂度为O(mn)，即它线性地依赖于数据矩阵的元素数目。

3.4 与其他模型的联系

本文提出的概率矩阵三分解算法本质上等价于根据极大后验法求解模型（5）。若令λ→0+，则算法1可用来求解基于l1范数的奇异值分解或主成分分析。与传统的概率矩阵分解模型相比，概率矩阵三分解多了矩阵S。当S为对角矩阵、且λs→+∞时，矩阵三分解就变成了二分解；当S为对角矩阵且sii可表示为伯努利分布与高斯分布之积时，矩阵三分解等价于稳定鲁棒主成分分析[30]。与奇异值分解相比，概率矩阵三分解模型不要求矩阵U和V满足列正交性，而且S也不是对角的。因此，概率矩阵三分解使得模型更加灵活实用。

还可以使用张量Tucker分解[31]来表示式（2），即：

其中，“×1”表示核心张量S与模式矩阵U的1-模式积，“×2”表示核心张量S与模式矩阵V的2-模式积。将矩阵三分解向量化，得到：

文献[32]提出了指数族张量分解，即假设vec(D)服从参数(V⊗U)vec(S)下的指数族分布，但此模型并未考虑U、S和V的先验分布。

4 数值实验

将鲁棒概率矩阵三分解应用到图像去噪及视频背景建模中。实验采用个人计算机，其处理器为Intel®CoreTMi5-7400@3 GHz，使用Matlab R2012a 进行编程。

4.1 图像去噪

采用人工方式合成一幅256×256的低秩图像（对应矩阵L），并在其上添加若干简单的英文单词（对应稀疏噪声矩阵E），从而合成含噪图像（对应矩阵D）[33-34]，如图1 所示。根据鲁棒概率矩阵三分解（RPMTF）来恢复低秩成分，从而得到噪声矩阵。在进行实验时，先将矩阵L、E和D的元素按相同的公式标准化到区间[-1,1]，再将英文单词对应的元素用[-0.5,1.5]区间上的均匀分布替换。

Fig.1 Synthesis of input image图1 输入图像的合成

使用低秩恢复误差和F1测度两种指标来度量算法的性能。低秩成分的恢复误差定义为，其值越小，低秩成分的逼近性能越好。记的绝对值最小元素和最大元素分别为Emin和Emax。对于给定的实数x，定义如下两个函数：

使用RPMTF 方法对前述合成的图像进行低秩与噪声成分的分离，并与PCP、RPMF、BRMF 和Tri-Decom 的结果进行比较。在RPMTF 参数设置中，取k=10，λu=λv=λs=λ=1，最大迭代次数为100。按照标准高斯分布随机初始化矩阵U和V，S的初始化矩阵为U†D(VT)†，其中“†”表示矩阵的伪逆。在RPMF 和BRMF 的实验中，仍取k=10，最大迭代次数为100，其他参数按照默认值设置。由于RPMF、BRMF、Tri-Decom 和RPMTF 的结果具有随机性，将实验重复20 次，最终报告实验结果的平均值与标准差。5种低秩矩阵恢复方法的实验结果如表2所示。

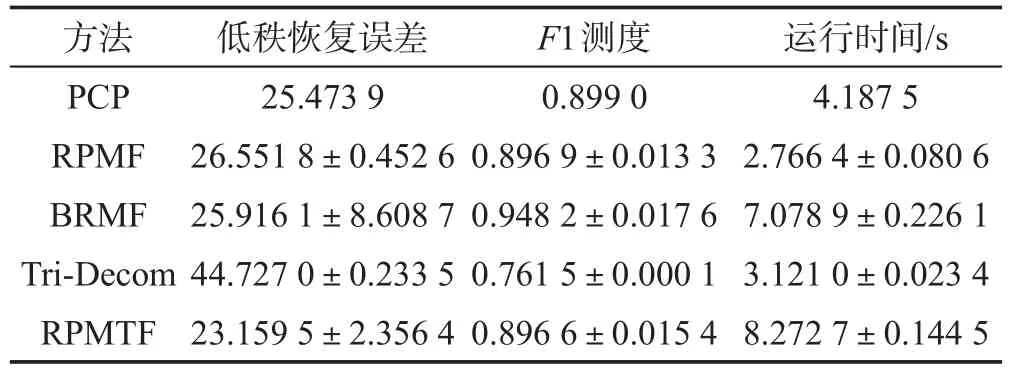
Table 2 Comparison of low rank matrix recovery results on synthetic images表2 合成图像的低秩矩阵恢复结果比较

从表2 可以看出：RPMTF 得到了最小的低秩恢复误差，Tri-Decom的恢复误差最大；BRMF取得了最大的F1 测度，RPMF 和RPMTF 得到了次优的F1 测度，Tri-Decom 的F1 测度最小；RPMF 的运行时间最短，RPMTF具有最长的运行时间。此外，BRMF低秩恢复误差的标准差较大，稳定性能较差。图2绘出了5 种方法得到的低秩图像与噪声图像，其中第1 行为低秩图像，第2行为噪声图像。从该图可以看出：Tri-Decom在低秩图像和噪声图像方面均具有最差的恢复性能，而BRMF 和RPMTF 都较好地恢复了低秩与噪声成分。

结合表2和图2可以得出如下结论：PCP和RPMF的低秩恢复误差较大，F1 测度较小，实验效果较差，这可能是由较小的k值所致；Tri-Decom 的恢复误差最大，F1 测度最小，实验效果最差，这可能是因为图像合成过程中没考虑稠密噪声；BRMF 和RPMTF 的恢复误差小，F1测度大，实验效果较好。

Fig.2 Low rank and noise images recovered by different methods图2 不同方法恢复的低秩与噪声图像

4.2 灵敏度分析

算法1涉及4个超参数{λu,λs,λv,λ}，其取值对实验结果产生一定的影响。下面以前述人工图像为例，探讨RPMTF方法中超参数不同取值对实验结果的影响。固定λ=1，取λu∈{1,7}，λv∈{1,7}，λs∈{1,7}。仍令迭代次数为100，重复实验20次。表3列出了平均实验结果，图3 显示了部分低秩图像与噪声图像。从表3和图3可以看出，RPMTF在一定程度上具有稳定性。

Table 3 Comparison of experimental results under different combinations of hyperparameters表3 超参数不同组合下的实验结果比较

Fig.3 Partial low rank and noise images under different hyperparameters(λu,λs,λv)图3 不同超参数(λu,λs,λv)下的部分低秩与噪声图像

下面考虑更多超参数取值对实验结果的影响。为简便起见，固定λu=λv=1，取λs=i/2,λ=j/2，其中i∈[10],j∈[10]。实验结果如图4所示。从该图可以看出：当λs≤4,λ≤4 时，低秩恢复误差与F1测度相对稳定。当λ比较大时，稀疏噪声的方差比较大，对恢复性能产生不利的影响。此外，当λs给定时，λ的取值对实验结果影响不显著。

4.3 视频背景建模

在Hall视频数据集上进行视频背景建模实验[34]。选取此视频序列的前200帧图像，其中每帧图像的大小均为144×176，部分图像如图5 所示。因此得到维数为25 344×200的数据矩阵。使用峰值信噪比（peak signal-to-noise ratio，PSNR）来度量算法的性能，其定义为：

Fig.4 Effect of different(λs,λ)on experimental results图4 (λs,λ)的不同取值对实验结果的影响

Fig.5 Partial images of Hall video图5 Hall视频的部分图像

Fig.6 Separation of background and foreground under different methods图6 不同方法下背景与前景的分离

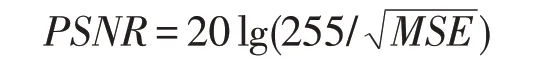
其中，MSE是真实背景和重建背景的均方误差。峰值信噪比越大，说明失真越少，实验效果越好。

在实验中，取k=5，最大迭代次数仍为100。对应于某帧图像，5种方法的背景与前景分离结果如图6 所示，其中第1 行为背景图像，第2 行为前景图像。从图6可以看出：前两种方法PCP和RPMF背景中还存在阴影，分离效果不理想；后3 种方法BRMF、Tri-Decom 和RPMTF 的实验结果比前两种方法好很多。5种方法PCP、RPMF、BRMF、Tri-Decom和RPMTF的运行时间（单位：s）分别为144.341 9、129.054 7、409.786 7、56.981 2、525.747 4，其中BRMF和RPMTF的运行时间较长，可以考虑采用并行计算策略。5种方法的峰值信噪比如表4 所示。从表4 可以看出：Tri-Decom的峰值信噪比最小，RPMTF的峰值信噪比最大，这说明RPMTF的实验效果最好。

Table 4 PSNR under different methods表4 不同方法的峰值信噪比

5 结束语

本文提出了概率矩阵三分解的一个鲁棒模型。为了简化模型求解，将拉普拉斯分布表示为高斯分布与指数分布的混合。基于极大后验策略，提出期望最大化算法。实验结果验证了所提模型的可行性与有效性。在建立模型时，仅考虑了U、S和V的元素服从均值为0的相互独立的高斯分布，对于其他的概率分布仍值得进一步研究。此外，鲁棒概率张量分解和基于变分贝叶斯推断的鲁棒概率矩阵三分解也将是今后的两个研究方向。