化动为定 化繁为简——以“与平面图形相关的数量积”复习教学为例

赵增辉

(江苏省溧阳市埭头中学，213311)

本文以“与平面图形相关的数量积”这一专题复习课教学为例,谈一谈学生对解题方法的选择．

一、课前预习

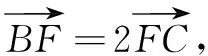
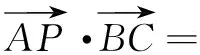
设计意图在一轮复习中，学生对于平面向量的数量积的定义,夹角,模等知识已经有了较深的认识,对定义法,基底法,坐标法等基本方法已能熟练运用,也初步掌握了研究向量问题的基本思想和方法,具备了一定的探究问题、分析问题和解决问题的能力.设计4个基础小练习,引导学生自主复习,目的是深化学生对基础知识,重要考点的理解、把握与梳理,为本节课问题的探究展开进行热身.题1意在巩固数量积的定义,也可利用投影知识(几何意义)来处理；题2围绕向量的投影法来设计,唤醒和巩固学生对投影法的理解,为例题做好铺垫;题3意在对投影法进行简单运用,设置一点障碍,让学生体会转化思想也可利用极化恒等式进行简单处理;题4意在巩固和复习极化恒等式的基本形式,为例题做好铺垫.

二、合作探究

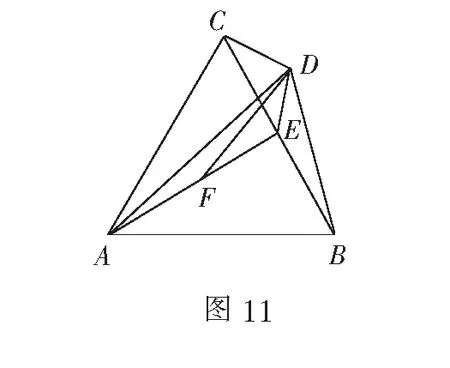
师:观察并尽可能用多种方法解决此问题;

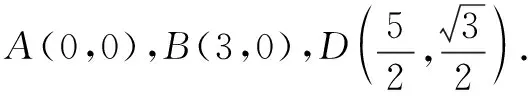
师:生1分别采用坐标法和基底法来处理此问题,那么这两种方法的理论依据是什么呢?

师:生1的解释非常好,请大家继续思考还有其他方法吗?

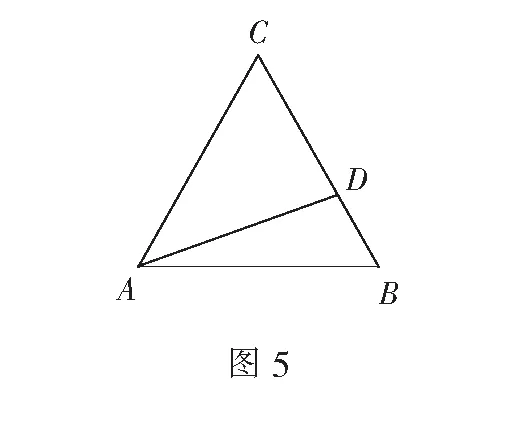
即AD2=AB2+BD2-2AB·BDcos 60°=7,

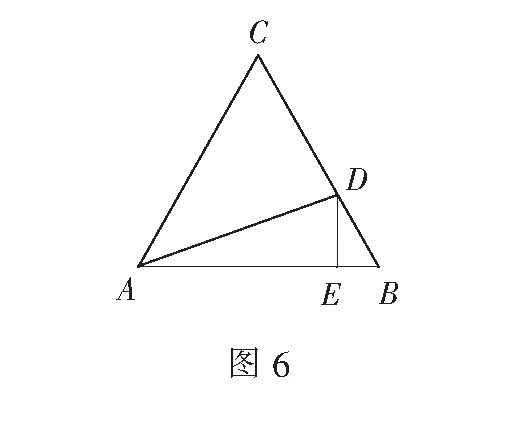
生3：利用投影法也能很快解决.如图6，只要过D作DE垂直于AB于E.

师:生2和生3的方法殊途同归,都是回归到向量数量积的定义(定义的几何意义)来解决.我们还有其他方法吗?课前预习4能给我们提供一些启示吗?

师:生4将向量数量积转化为三角形中线与边长的关系,我们把这种关系称为极化恒等式.我们能否用文字语言和符号语言来表示这种关系呢?

生5:共起点的两向量的数量积可表示为对应三角形中线与第三边一半的平方差.

师:思考中线与第三边和所给向量之间的关系，我们能看出什么?

师:如果我们把所求向量的数量积表示为a·b,那么a·b可以如何表示?

师:很好,这就把两个向量的数量积转化为两个向量模的等式.我们能小结一下求向量数量积的方法吗?

生7:我们可以利用坐标法、基底法、定义法、投影法和极化恒等式来处理两个向量的数量积.

师:我们可以看到这五种方法中,坐标法,定义法,投影法都是直接去解决数量积问题,我们称之为直接法.而基底法和极化恒等式方法,则是将所求向量转化为其他已知向量或者数量的平方差，我们称之为间接法.

设计意图通过一题多解，进一步巩固学生前面复习的基本方法,引导学生积极思考,深度探究投影法.

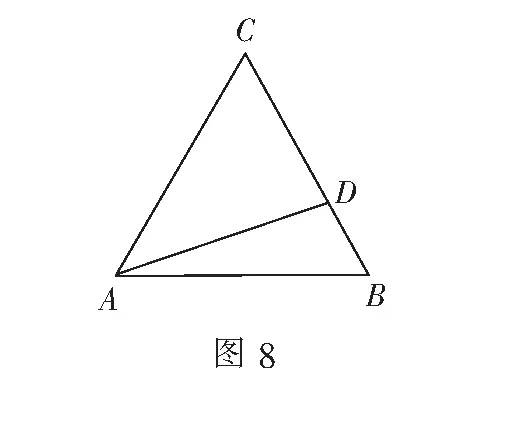
师:观察上式与问题1的变化,并给出合理解答.

师:在多种方法可选的情况下,我们看到投影法是最简便的方法．

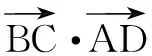
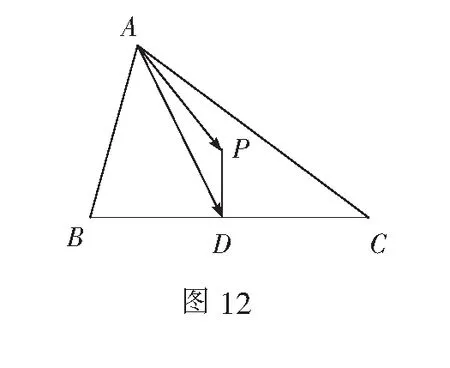
师:观察上式与变式1的不同,并给出恰当解答.

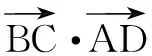
师:在不同情境下运用相同方法,变中寻不变,很棒！我们再变形一下:

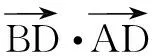
师:这又与变式2有什么不同呢?该怎样解答呢?

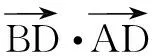
生6:我觉得他的这种方法并不是最好的,如果利用极化恒等式会更加方便.

师:很好,刚才生6将数量积问题通过极化恒等式转化为向量模的范围运算,大大简化了运算量.

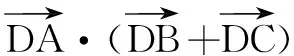
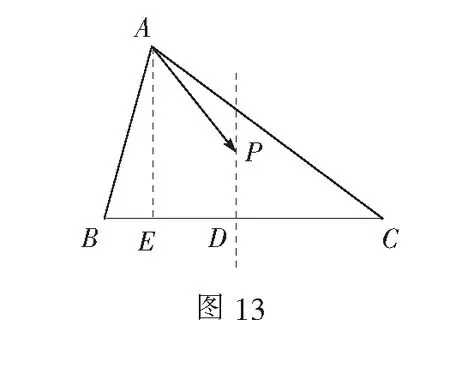
师:这又与变式3,有什么不同呢?这又该怎样解答呢?

生9:我发现点D的运动已不在直线BC上,点D在平面内运动了.问题也变成求有关三个向量的数量积问题了.

师:我们可以讨论一下,看看突破口在哪儿?

师:恰当运用极化恒等式,可以实现“秒杀”!当然本题利用坐标法也可以解决.

设计意图通过对问题1的4个变式的设计,一题多变,意在对向量方法的活学活用.向量投影的应用,可以极大地简化过程.极化恒等式的优点在于可以很好地利用已知条件,运用转化思想,把复杂的动点问题和几何问题转化为定点问题和简单的代数问题，避免了中间代入的繁琐过程,准确快速地解决问题.当然,它也有较大的局限性,总要和中点相关．

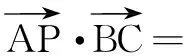
师:请进行小组交流,给出解决方案.

师:很好！利用极化恒等式的变形,将数量积转化为已知量的代数问题.

生11:利用刚才相同的方法可以得到结果是不变的还是6.

师:非常好,那么根据前面两个问题,你能提出更一般的结论吗?

师追问:能说明理由吗?

师:两位同学从不同角度解释了这一结论,可谓殊途同归,十分精彩.

设计意图在无法用坐标解决的情景下,合理选择恰当的方法来解决数量积问题,通过转化思想,将未知量转化为已知量,将动点问题转化为定点问题,体现了“化动为定”的思想方法.最后设计开放性问题,即可拓宽学生思考问题的视角,还可进一步培养学生从特殊到一般的思维方式.

三、课堂小结

通过本节课的学习,你有哪些收获呢?

知识总结:平面向量数量积的常见求解方法,特别是投影法和极化恒等式法的合理运用.

方法总结:从问题情境出发,从已有知识出发,合理选择恰当方法.

思想总结:转化与化归,函数与方程,数形结合.

设计意图课堂小结不仅是让学生反思课堂所学,更是培养学生学习——总结——学习——反思的良好习惯,同时也可以通过自我评价来获得成功的快乐,提高学生学习数学的自信心,培养学生用数学的语言来表达,从而提升数学核心素养.

四、教学反思

数学学习追求的不仅仅是把题做“对”,更看重的是把题做“好”,即追求解题策略的“最优化”.为此我们不仅要掌握平面向量数量积的基本方法,更要在面对具体问题时,能够迅速做出判断,选择最优化解题策略,这是学生能力的体现.要培养这样的能力,需要丰富的学习经历和经验的积累,而不是简单的模仿.以笔者之见,知识不是教会的，而是学生学会的.学习应该是学生亲力亲为的事,别人无法代替.