高考几何题的“高观点”求解及思考
毛润东 濮安山
(江苏省扬州大学数学科学学院,225002)
利用高等几何中的交比知识以及仿射几何的知识来解高考向量问题和解析几何问题,可为解决初等几何问题拓宽思路.本文对此作一些探讨.
一、利用交比性质突破难点


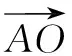
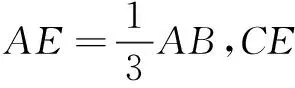
三等分线与中线交点将中线分成两条线段,这两条线段与中线有一定的比例关系,要求这种比例关系,可以选择建立坐标系.但又由于建立坐标系需要进行较为复杂的计算,所以这里引入交比法来突破难点.

交比的初等几何意义是:如果限于欧氏平面,则交比等式右边的P1P3,P2P4,P2P3,P1P4就是两点间的有向距离.
性质1[2]两点列成射影对应的充要条件是任意四点的交比与对应四点的交比相等.
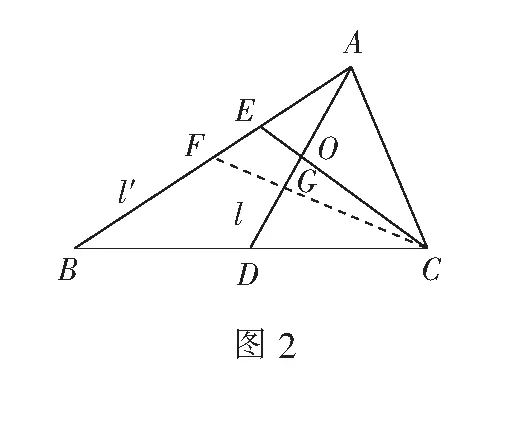
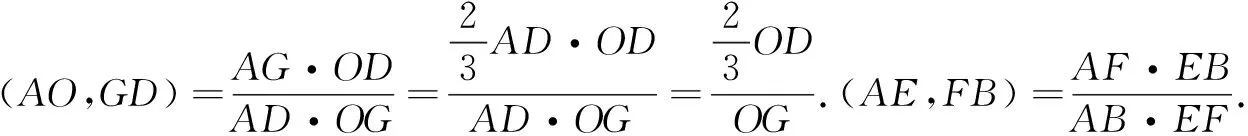
据此,易得例1的解法如下:

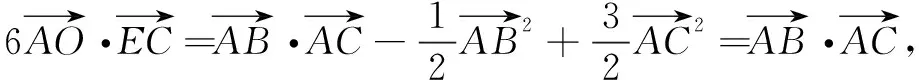
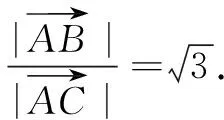
评注运用交比证明的理论依据就在于交比的初等几何意义:在欧氏平面中等式右边的四个因式都是两点间的有向距离,又因为交比符号中四个点是对应点,只需要考虑线段的长度即可.证明过程首要的就是选取透视中心(例题中选取C),根据中心投影构造两点列的透视对应.作辅助线中线的原因有二:一是构造出透视对应点列的四点,根据充要条件这四点与对应四点交比相等;二是能够直接利用三角形重心将中线分成长度比为1∶2的线段这一性质.可以看出运用交比法证明,过程较为简单与直接.
二、利用圆的几何性质简化问题
在笛卡儿直角坐标系下,任意一个椭圆经过仿射变换后的对应图形为圆.利用椭圆的仿射性质,将椭圆中的点、线元素变为圆中的元素,然后利用圆的几何性质解题,就能起到简化作用.

(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.
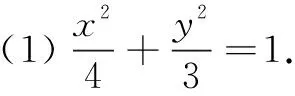
(2)方法1因为直线AE的斜率与AF的斜率互为相反数,所以直线AE与直线AF的斜率都存在,所以不妨设AE的斜率为k.


用-k代替k,可得点F的坐标


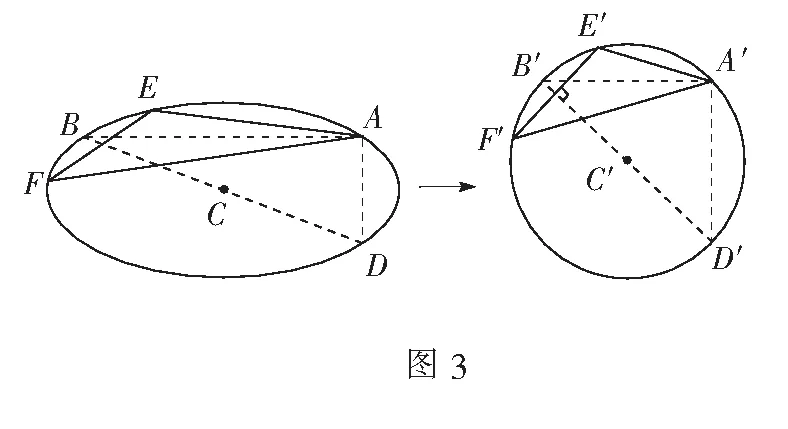
评注这是一类求椭圆弦的斜率为定值的问题.对比这两种方法,显然方法2更加简单,方法2可以避免复杂的计算.方法1中如果点的坐标不是简单的整数与分数的话,联立方程的复杂程度将更高.方法2利用仿射变换将椭圆中的弦EF变为圆中的弦E′F′,BD变为圆中的直径B′D′,且B′是弧E′F′的中点,然后利用经过弧中点的直径与弧所对应的弦垂直这一圆中的性质,就能很快地解出该题.
——书写要点(三)

