探析核心素养视角下的数学高考
——以2019年全国理科Ⅰ卷为例
郭延鹏
(河南大学数学与统计学院,475004)
《普通高中数学课程标准(2017版)》以学生发展为本,为了落实立德树人的任务,提出了六大数学学科核心素养.本文以2019年全国理科数学I卷为例,分析新课标提出的数学学科核心素养的考查情况,供大家参考.
一、试题分析
1.对数学抽象的考查
数学抽象的实质是数学发现和数学创造.教好数学抽象、学好数学抽象并不是一件容易的事情, 唯有在实践中上下求索、不断优化和改进[1].试题中有多题考查了数学抽象核心素养,如第4、6、13、15、17、22题.现以第4题为例:

(A)165 cm (B)175 cm
(C)185 cm (D)190 cm
该题以学生耳熟能详的“断臂维纳斯”石像为情境,注重考查学生将实际问题抽象成数学问题的能力,具体考查的知识点并不难.通过高中课程的学习,学生积累了一定的活动经验,抽象思维水平得到提高,逐步学会了用数学知识解决日常生活中存在的问题.试卷中通过具体的题目考查学生的数学抽象核心素养,体现了素质教育引领下的立德树人的根本任务.
2.对逻辑推理的考查
试题中有多题考查了逻辑推理核心素养,如第1、18、19、20、21、23题,现以第1题为例:
已知集合M={x|-4 (A){x|-4 (B){x|-4 (C){x|-2 (D){x|2 该题以集合知识为载体,考查集合交集和一元二次不等式的学科知识,学生要针对该题进行逻辑推理,利用数形结合的思想正确解出不等式,进而通过集合的运算得出最终结果.这个题目还对学生的数学运算提出了一定的要求.通过高中数学课程的学习,学生能掌握逻辑推理的基本形式,学会有逻辑地思考问题,能够在比较复杂的情境中把握事物之间的关联,把握事物发展的脉络,形成重论据、有条理、合乎逻辑的思维品质和理性精神,增强交流能力[2]. 新课标整合了课程内容,使内容更加情景化.随着社会的发展,数学极大地拓展了其应用领域,新课标中多次提到数学和实际生活息息相关,所以数学建模核心素养对于学生非常重要.现以试题中的第21题为例: 为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X. (1)求X的分布列. (2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=p(X=-1),b=p(X=0),c=p(X=1),假设α=0.5,β=0.8. (i)证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列; (ii)求p4,并根据p4的值解释这种试验方案的合理性. 这是一道以生物实验为载体的应用题,综合考查了概率统计、排列组合、数列等学科知识,同时考查复杂式子化简、综合计算等基本技能,并对学生分析问题的能力提出了较高的要求. 第(1)问要求学生能根据题干中给出的条件抽象出数学模型,分析得到X的取值只有-1,0,1三种,然后列出X的分布列.第(1)问重在基础知识的掌握,主要是考查学生分析问题解决问题和建立数学模型的能力. 直观想象并不等同于数形结合,其重在用空间形式分析问题,并建立起它们之间的联系从而解决问题,直观想象是抽象思维形成的基础.在2019年全国I卷中,着重考查了直观想象核心素养,如第3、5、7、10、11、12、13、16、17、18、19题,现以第11题为例: 关于函数f(x)=sin |x|+|sinx|有下述四个结论: ①f(x)是偶函数 ③f(x)在[-π,π]有4个零点 ④f(x)的最大值为2 其中正确的结论的编号是( ) (A) ①②④ (B) ②④ (C) ①④ (D) ①③ 该题以正弦函数为载体,综合了三角函数和绝对值的相关知识,考查了学生对分段函数图象的掌握程度.解题过程中首先通过分析题意去掉绝对值,将原函数转化为分段函数,然后进行直观想象作出该函数的草图,最后确定函数的相关性质与特征.通过高中数学课程的学习,学生能提升数形结合的能力,发展几何直观和空间想象能力,增强运用几何直观和空间想象思考问题的意识,形成数学直观,在具体的情境中感悟事物的本质[2]. 数学运算在解决数学问题时不可避免,计算能力体现了一个学生最基本的数学素养,是解决数学问题并得到最终正确结果的保障.试卷中有大量涉及数学运算核心素养的题目,如第1、2、4、6、9、10、12、13、14、16、17、18、19、20、21题,现以第14题为例: 大数据时代已经到来,用“数据爆炸”一词来形容如今的互联网也不为过.为了适应时代的快速发展,培养学生的数据分析核心素养就显得尤为重要.试卷对数据分析也有考查,现以第8题为例: 该题以程序框图为载体,考查学生对程序框图各部分结构的理解,在解题过程中要求学生准确地分析所给的数据,每循环一次流程图,就得到一组数据,一直循环下去,直到得到所需数据,在对数据进行分析的时候要足够严谨不允许有丝毫的差错,数学学科本身的特点要求学生必须养成认真求实的科学精神. 为了方便比较分析,现将2019全国I卷各核心素养的考查情况汇总于下表: 考查素养的类型数学抽象逻辑推理数学建模直观想象数学运算数据分析 题号4,6,13,15,17,221,18,19,20,21,23213,5,7,10,11,12,13,16,17,18,191,2,4,6,9,10,12,13,14,16,17,18,19,20,218 题目数量66111151 由上表可以发现: (1)试卷对于直观想象和数学运算核心素养的考查要远远多于对其他核心素养的考查. (2)试卷考查了学生发现和提出问题、分析和解决问题的能力,在注重基础知识的考查中又侧重于试卷整体的创新.近些年来,首次将概率统计和数列综合到一个题目中,并且将其作为最后一道压轴大题,这也恰恰符合新课标的素养导向.整张试题强化了对数学学科核心素养的考查,这说明高考已经由“唯知识论”开始转向“素养导向”. (3)试卷增加了综合型的题目,一道题目往往涉及多个核心素养的考查.语言描述类型的试题有所增加,例如第4、6、21题.题干采用较长的篇幅,将现实情境和数学知识融合在一起,以评价学生的综合素养.3.对数学建模的考查

4.对直观想象的考查

5.对数学运算的考查
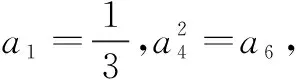
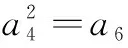
6.对数据分析的考查
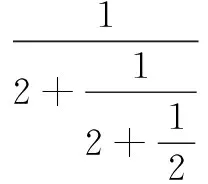

二、数据分析