强化联系观点 提升数学素养
——基于“唯物辩证法联系观”的教学实践与认识
孔德鹏
(江苏省南京航空航天大学附属高级中学,210007)
唯物辩证法,是研究自然、社会、历史和思维的哲学方法. 唯物辩证法的范畴是对事物、现象间最普遍的辩证联系或关系的概括和反映,是辩证思维的逻辑形式. 联系的观点是唯物辩证法的一个总特征,是人们考察事物、分析问题的基本原则.
从数学的育人价值来看,经常渗透和强化唯物辩证法的联系观等哲学观念可发展思维和认知力,对学生形成正确的价值观、世界观和人生观有独特作用,为学生用数学与世界交流提供方法论,提升学生的数学素养.
一、运用“联系的普遍性”挖掘数学本质
恩格斯说,辩证法是关于普遍联系的科学. 所谓联系就是事物之间以及事物内部要素之间互相依赖、互相影响、互相制约和互相作用. 联系是普遍的,世界是普遍联系的,数学“世界”也是如此,没有一个数学公式、概念是孤立的. 教学就是要揭示这种普遍的联系,利用这种普遍联系,生成新的事物,推进数学理论的更迭.于过程中渗透联系观,教学生用“联系的”数学眼光看问题,教学生掌握学习数学的方法论.
案例1“函数的零点”教学
在“函数的零点”教学中,首先给出一个不能用公式求解的方程lgx=3-x. 启发学生思考:这个方程有没有解?能不能用公式求解?解的具体数值是多少?学生自己提出画图,有两种情况:一种是画出y=lgx与y=3-x图象,发现只有一个交点,对应着方程只有一个解;另一种是画出y=lgx+x-3图象,发现与x轴只有一个交点. 这样,不管是学生画两个函数图象还是一个函数图象,学生都自然想到了函数,此时教师要抓住这个闪光点,再启发引导抽象出函数零点的概念. 这样的教学安排基于尊重学生认知,让学生提出问题,实现了静态的方程向动态的函数的转变,通过函数零点概念的学习,抓住了本质——方程只是函数值为0的一种特定形态!这样的教学安排,加深了对方程与函数关系的认识,提升了研究事物联系的观点. 甚至进一步注意到不等式、方程与函数三者之间也有着密切关系.教学中要教给学生用“联系的眼光”辩证地看问题,抓住问题本质,把不等式、方程都放在函数的下面,实现函数统领代数的大思想的深化,渗透对学生的辩证唯物主义教育.
二、运用“联系的客观性”发展理性精神
辩证唯物主义认为,联系是客观的. 联系是事物固有的特征,不以人的意志为转移.在实际教学中,渗透数学对象联系的客观性的哲学观点,培养学生不偏不倚、理性客观的精神,强化从数学对象固有的联系中把握事物,善于抓住事物的真实联系.利用联系的客观性可以发展学生的理性精神,提升理性思维能力.
案例2期末试卷讲评
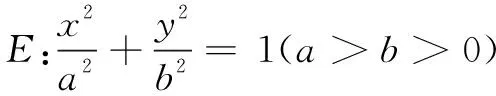
(1)求椭圆E的方程;
(2)若BC⊥CD,求k的值.


三、运用“联系的多样性”培养发散思维
事物的联系是多种多样的,有直接联系、间接联系、内部联系和外部联系、本质和非本质联系、必然联系和偶然联系等.数学教学要渗透把握联系多样性的哲学思想,对正确认识事物有重要意义.正如波利亚所说:“好问题同某种蘑菇有些相象,它们都成堆地生长,找到一个以后,你应当在周围找找,很可能附近就有好几个.” 要培养学生发散思维和开阔的数学视野,从不同视角分析问题、解决问题的能力.应当鼓励多元价值并存,激励学生勇于创新.引导学生剖析不同问题、不同方法之间的联系性,深入把握数学本质,提升认知力.
案例3不等式例题教学

学生给出以下三种解法.



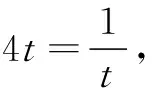


例题乍看无从下手,变量x,y之间似乎没有什么直接联系,而这恰恰对学生辩证联系地看问题以及发散思考问题提出了较高要求. 对于这个“分式”结构引发了学生联想和联系的处理问题经验:将分式通分是常用方法.这不只是一个简单的分式——齐次式,通过换元进行消元,转化为一元函数求最值.分母比较复杂时还可用整体换元解决,将复杂问题简单化,转化为熟悉的场景.而这些都需要学生冷静观察、积极联想、细致的计算等“火热”的思考活动.通过这样一道题目,从不同结构不同方面进行挖掘,突出联系性,寻找问题突破口,实现了发散思维的训练.
在数学教育中,教学内容在整体系统的思想下互相贯通,是一个统一的关系网,它自始至终将启迪思想、开放智力作为追求目标. 弗赖登塔尔也曾言:“重要的并不在于一个人所学的数学是被记住了还是被忘记了,而是在于它是否仍然具有活力,是否能起作用,这同样是个人生活与人类历史的规律. 要保证有活力,就必须教给学生充满着联系的数学.”教学中不应为了教概念而教概念,应该注重概念间的联系,注重知识的前呼后应,加强数学内部的纵向联系、学科间横向联系、加强数学基础和数学方法的联系.利用唯物主义辩证法作为思想武器,从“联系的普遍性、客观性、多样性”深化对学生学习的认识,为培养学生的数学核心素养助力!

