基于HPM的数学公式生成

陈 蓓

(江苏省南通中学，226001)

数学史融入数学教学的研究，是数学教学研究的重要组成部分,也是 HPM(History and Pedagogy of Mathematics的缩写,意为数学史与数学教育) 研究的重要方向之一.将数学史融入数学教学,离不开基于数学史料的数学问题的提出.

笔者有幸参加了由江苏省教研室组织的青年教师优课评比,并获得了一等奖.在本次比赛中,笔者以苏教版《数学》必修5第二章第2节的“等差数列的前n项和”第一课时为课题,上了一节基于HPM的公式生成课.下面介绍本节课的教学过程及笔者的教学反思.

一、 借助史料,引入课题

师:数学在故事中,故事在历史中.本节课,让我们沿着历史的足迹,寻找数学故事,感受数学之美.在我国数学巨著《九章算术》中有这样一个故事:“今有良马与驽马发长安至齐,齐去长安三千里.良马初日行一百九十三里,日增十三里;驽马初行九十七里,日减半里.复还迎驽马,问几何日相逢.”这是一个怎样的数学问题呢?

生:等差数列.

师:这个等差数列的首项是什么?公差是多少?我们说:良马逐日的行程数构成了一个以193为首项,13为公差的等差数列.此时,根据等差数列的通项公式,我们可以求出良马前15日的逐日行程数(略).

师:接下来,你还能继续研究什么数学问题吗?

生:求良马前15日行程总和.

师:这就是我们今天要研究学习的“等差数列的前n项和Sn”.

二、 展开问题,探索新知

师:下面我们就来研究这个故事中良马前15日的总行程S15=193+206+…+375=?

生:可以一个一个相加.

师:当然可以.但是计算起来比较麻烦,而且如果要求前100日的总行程就不太好办了.有没有更好的办法呢?

师:这种计算方法对吗?这个式子蕴含了怎样的数学道理呢?你想知道中国的古人是怎样解决这个问题的吗?其实,我国古代数学家杨辉早在高斯之前500多年就在《详解九章算法》中给出了解决方法.他画了这样一个条形图(图1),其中每一个条形的长度表示“良马”每日的行程数:

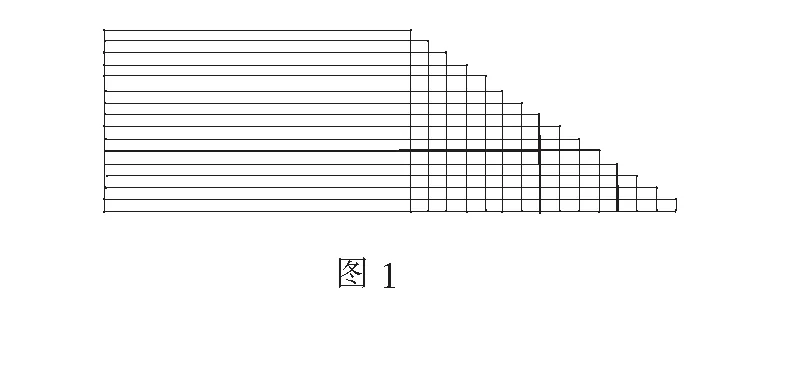
第一天的行程数用长为193的条形表示,第二天的行程数用长为193+13的条形表示,以此类推…良马前15天的行程数用这个图表示.这样,求“良马”前15日总行程即求什么?

生:这15个条形的长度之和.

师:下面请同学们沿着古人的足迹,借助手中的“良马图”，求一求“良马”前15日的行程总和S15.请小组展开讨论.

生:我们发现“良马”前15日的行程都具有共同的193,于是先将这部分割出来,求得这部分长度之和为15×193,剩余的部分补成相同的14×13(图2).

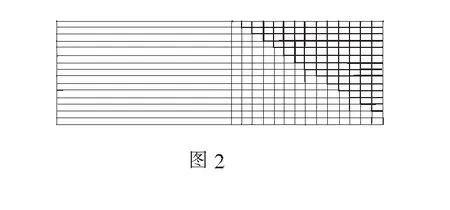
师:为什么要补呢?

生:因为补成相等的数,求和比较容易.

师:好的,接下来你们有什么发现?

师:很好!这组同学将不等数的求和通过“补”的方法转化为了相等数的求和.这实际上就是我国数学家杨辉在《详解九章算术》中的方法.

师:我发现有一组同学采用了另一种方法,请这位同学来展示一下(学生演示)

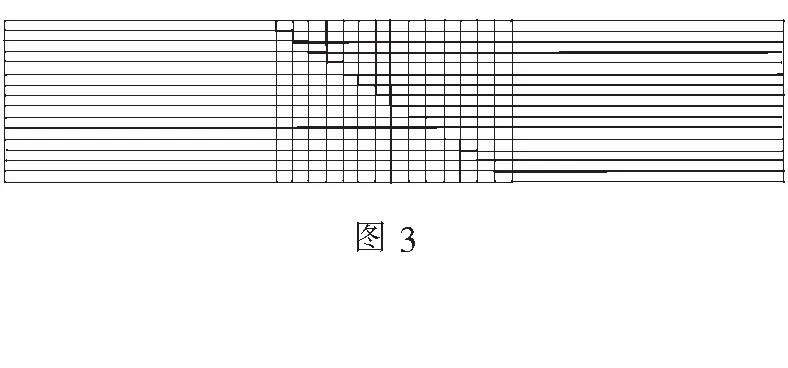
师:这种方法也很好,这是在小学时同学们就已知道的数学家高斯的一种求和方法,其实他落后我国数学家杨辉500多年呢!

三、归纳提升,生成公式

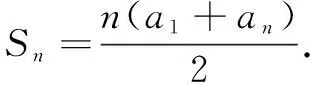
师:你能类比刚才我们将“良马图”倒过来求和的方法,来论证这个结果吗?(学生回答,老师补充)

图3的左边表示的是以a1为首项,公差为d的等差数列的前n项和:

Sn=a1+a2+…+an

=a1+(a1+d)+…+[a1+(n-1)d].

而右边则表示的是以an为首项,公差为-d的等差数列的前n项和:

Sn=an+an-1+…+a1

=an+(an-d)+…+[an-(n-1)d].

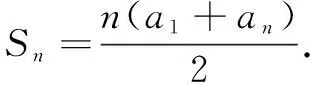
这种证明公式的方法称为“倒序相加法”.你们还能由另一种求和方法得到等差数列{an}的另一个前n项和公式吗?

师:能借助刚才的第一个公式快速证明这个结果吗?

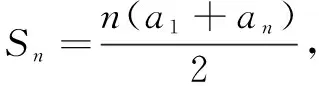
四、 应用新知,解决问题

例1在等差数列{an}中,完成下表:

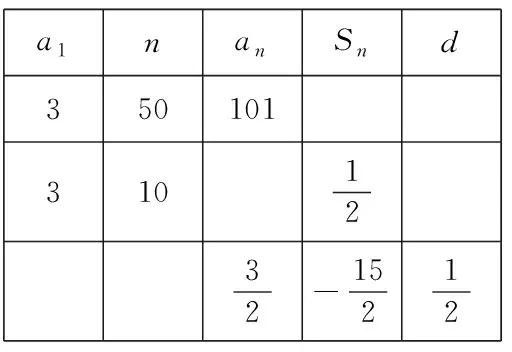
a1nanSnd3501013101232-15212

师:如果已知了a1,n,an,如何求Sn呢?如果已知了a1,n,d,又如何求Sn呢?

生:直接使用两个公式.

师:对于第三个问题,无法直接使用公式,你如何解决呢?

生:借助两个求和公式和通项公式,列方程组求解.

师:观察公式,这三个公式中都体现了四个量之间的关系,代入已知的三个量,都可以得到a1和an的一个等量关系.因此，只需在两个求和公式和通项公式中任意选择两个公式组成方程组,即可求得.

师:在本题的运算过程中,你有什么感悟吗?

生:在等差数列的五个基本量中,已知了其中的三个量,就能求出剩下的两个量.

例2在等差数列{an}中,已知前10项的和为310,前20项的和为1 220,求前30项的和.

师:为了求S30,由两个条件,通过求和公式列方程组,先求出首项和公差两个基本量,从而转化为“知三求二”(由条件发现S10,S20-S10,S30-S20成等差数列).这是偶然还是必然呢?请同学们课后思考.

五、 课堂小结,首尾呼应

师:这节课,我们通过“良马与驽马”这个故事中“良马”的行程问题,研究了一种求和方法，得到了两个求和公式;通过从“良马图”的形的观察,到代数论证,体会了数形结合的思想；通过“补”的方法，将不等数的求和问题转化为相等数的求和问题,体会了转化化归思想；通过列方程组解决等差数列中基本量的问题,体会了函数方程思想.

师:今天这节课我们只研究了“良马”的问题,这个故事中,良马先到达了齐,又折回去迎接驽马,这两匹马何时会相逢呢?请同学们课后继续研究.

“基于数学史的问题导入”是HPM视角下的数学教学的需要.问题串的使用将更完整地再现公式的发生和发展历史,使数学史的教育价值得以最大化.此外,基于数学史的问题导入并非易事,需要教师从众多数学史文献中选择恰当的史料.但是，我们有理由相信,基于数学史问题导入的广泛使用，必将使得HPM的研究水平迈上一个更高的台阶.