基于模拟退火的多尺度岩心三维图像融合重建
孙本耀, 滕奇志, 冯俊羲, 李 洋
(四川大学电子信息学院, 成都 610065)
1 引 言
在石油地质研究中,油气主要储存在储层岩心的孔隙中,孔隙的微观结构直接影响着油气的储量及运移能力[1],因此,研究孔隙微观结构具有重要的意义.
近年来,采用计算机断层扫描(CT)获取岩心序列切片图像并构建三维图像的方法逐渐得到应用,但由于成像机理的限制导致CT扫描图像在成像视域和分辨率之间存在矛盾.在传统石油地质研究中,一般利用全直径岩心或柱塞状岩心开展物性实验,因此也希望得到相应视域的三维结构图像,但由于CT图像分辨率的不足,导致无法完全表征微米级尺寸的小孔隙.为了获取微米级及以下小尺寸孔隙结构的清晰图像,只能将岩石切割成几毫米甚至更小的样本,这在一定程度上导致了样本的代表性有所欠缺.另一方面,在岩心分析研究中,通过对岩心薄片的光学显微镜成像以及岩石样本的扫描电镜成像等,高分辨率二维岩心图像的获取相对容易和普遍,且基于二维岩心图像的三维重建研究已比较成熟[2-5].因此,我们考虑,利用易获取的高分辨率二维岩心图像,借鉴三维重建算法,将高分辨率图像的小孔隙信息与低分辨率CT图像进行融合,以获得较大视域的高分辨率图像.
目前,有不少学者在多尺度岩心图像融合方面开展了研究,Okabe和Blunt[6]使用了两组不同尺度的图像.将低分辨率3D X射线图像作为基础,并且随机地重建2D高分辨率图像中所示的亚微米级孔隙,结合其中可以观察到的小规模和大规模信息作为最终的重建结果.Tahmase[7]等人使用来自两种不同分辨率的2D图像,分别建立了纳米级和微米级模型并叠加,合成了同时具有纳米级孔隙和微米级孔隙的3D岩心图像.这种直接叠加的方法可能使岩心三维结构中部分小尺寸孔隙被大尺寸孔隙完全覆盖,导致使岩心的孔隙度发生较大偏差.本研究提出了一种基于模拟退火算法将高分辨率二维岩心图像与低分辨率三维岩心融合重建为高分辨率三维岩心的算法.
2 算法详解
2.1 模拟退火算法简介
模拟退火算法是1953年由Metropoli依据金属冶炼中退火原理提出,1983年由Kirkpatric[8]将其成功应用于求解组合优化问题中.1997年Hazlett[9-10], Yeong和Torquat等人[11]将其应用到三维随机重建中.模拟退火算法有效地避免了迭代过程中容易出现局部最优化的现象.并且当重建结构的目标函数收敛于二维图像的目标函数时,重建结构中一定会呈现出目标函数所描述的特征.
2.2 基于模拟退火的多尺度岩心图像融合重建
算法以低分辨率三维岩心为基础,低分辨率三维岩心中孔隙为硬数据,基于模拟退火算法,将高分辨率训练图像中的小尺寸孔隙结构直接融合重建在低分辨率三维岩心结构中,实现低分辨率岩心到高分辨率三维岩心的融合重建.
2.2.1 岩心图像预处理 我们先对不同分辨率岩心图像进行定标,一个像素(体素)的长度称为点长度,假如低分辨率岩心图像的点长度是高分辨率岩心图像点长度的N倍,则需要将低分辨率三维岩心通过插值放大以统一两者点长度[12],低分辨率三维岩心中的每个体素最终在融合重建结果中占据N3个体素.
高低分辨率图像的孔隙尺寸可能有重复,因此首先在低分辨率三维结构中随机抽取多张岩心图像,统计其二维岩心图像的平均孔隙分布情况,去除高分辨率二维岩心图像中重复含有的大尺寸孔隙结构,以此作为高分辨率训练图像,指导低分辨率岩心的融合重建[13]过程.
2.2.2 模型建立 该算法模型的建立主要由解空间、目标函数和初始解三部分组成[14].在本研究中我们采用了两点相关函数作为目标函数,算法开始迭代的起点为初始解,解空间是在低分辨率三维结构的基础上根据二维高分辨率训练图像中小尺寸孔隙的比例所组成的三维结构.
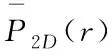
(1)
式中,E的值越低说明低分辨率三维结构中融合重建的小尺寸孔隙的相关函数分布和高分辨率二维训练图像越接近.
2.2.3 状态产生函数和接受函数 基于模拟退火的多尺度岩心图像融合重建算法按随机的方式产生新状态:将低分辨率三维结构中的孔隙作为硬数据点不做任何改动,在剩余的三维结构中随机选择不同相的两个像素,交换它们的相,得到新状态,保证三维结构中各种成分所占比例不变.计算新状态的能量E′和旧状态的能量E的差值:ΔE=E′ -E,并按Metropolis准则接受新状态[15].

(2)
其中,T是温度,其初始值和变化速度由冷却进度表决定.
2.2.4 实验流程 为了验证算法的有效性,需要对同一岩心分别获取高低分辨率三维图像,并对低分辨率三维岩心的融合重建结果与高分辨率三维岩心进行定量分析和视觉效果的比较.但在实际中,对同一岩心分别进行高低分辨率扫描并进行准确的配准很难实现.因此,在本验证实验中,利用已有的CT扫描高分辨率三维岩心图像,对其进行下采样模拟得到与其对应的低分辨率三维岩心图像.在高分辨率图像中去掉大尺寸孔隙,在留下小尺寸孔隙的序列图像中选取二维岩心图像作为待融合的训练图像.融合重建算法流程图如图1所示.图1中具体流程步骤如下.

图1 基于模拟退火的多尺度岩心图像融合重建实验
Fig.1 Multiscale core image fusion reconstruction experiment based on simulated annealing
(1) 在真实CT高分辨率岩心图像中选取一张高分辨率二维岩心图像.将高分辨率三维岩心图像进行下采样模拟得到低分辨率岩心图像.
(2) 将低分辨率三维岩心图像进行插值放大,使其与高分辨率二维岩心图像的点长度相同.统计低分辨率三维岩心图像二维切片的孔隙分布,记录其最小孔隙尺寸.统计二维高分辨率岩心图像的孔隙分布,只保留孔隙尺寸小于低分辨率图像最小孔隙尺寸的孔隙,以此作为二维高分辨率训练图像.
(3) 将低分辨率三维岩心图像中的孔隙相作为硬数据,在重建过程中不做改变.根据二维高分辨率训练图像的孔隙度在三维低分辨率岩心图像的岩石相中随机布点,将其设置为初始状态,并设定初始温度.
(4) 随机选取岩石相和随机布置的小孔隙相并进行交换,产生新状态.
(5) 计算新状态与旧状态所对应的目标函数差△E,并依据Metropolis准则判断新状态是否被接受[16]:若△E≤0,则接受新状态作为新的当前状态;若△E>0,则以概率exp(-△E/T)接受新状态作为当前状态.
(6) 重复步骤(4)和步骤(5),直至交换次数大于设定的门限值或三维结构的能量低于设定值[16],高分辨率三维岩心融合重建完成.
3 实验结果及分析
在本实验中,样本1的CT扫描高分辨率三维岩心图像如图2(a)所示,分辨率为10 μm/px,尺寸为256 px×256 px×256 px.通过下采样模拟得到与其对应的CT扫描低分辨率三维岩心如图2(b)所示.图2(b)分辨率为20 μm/px,尺寸128 px×128 px×128 px,分辨率与样本1高分辨率三维岩心相差2倍.样本2的CT扫描高分辨率三维岩心图像如图2(c)所示,分辨率为10 μm/px,尺寸为256 px×256 px×256 px.通过下采样模拟得到与其对应的CT扫描低分辨率三维岩心如图2(d)所示.图2(d)分辨率为40 μm/px,尺寸64 px×64 px×64 px,分辨率与样本2高分辨率三维岩心相差4倍.

(a)样本一高分辨率图像 (b) 样本一2倍低分辨率图像 (c) 样本二高分辨率图像 (d) 样本二4倍低分辨率图像
图2 岩心三维图像
Fig.2 3D core image
图3(a)是在图2(a)所示样本一高分辨率岩心图像中获取的一张高分辨率二维岩心图像,分辨率为10 μm/px,尺寸为256 px×256 px,作为样本一高低分辨率2倍融合重建实验的待训练图像.图3(b)是在图2(c)所示样本二高分辨率岩心图像中获取的一张高分辨率二维岩心图像,分辨率为10 μm/px,尺寸为256 px×256 px,作为样本二高低分辨率4倍融合重建实验的待训练图像.由于低分辨率岩心图像和高分辨率二维岩心图像分辨率不同.因此需要将低分辨率三维岩心图像进行插值放大,以统一低分辨率三维岩心和高分辨率二维岩心图像的点长度.

(a)样本一2倍融合重建实验待训练图像. (b) 样本二4倍融合重建实验待训练图像
图3 高分辨率待训练图像
Fig.3 High resolution training image
样本一低分辨率三维岩心图像二维切片的孔隙分布和高分辨率二维岩心图像的孔隙分布如图4(a)所示.根据两者的孔隙分布对比,在低分辨率岩心二维切片图像中直径小于20 μm的孔隙不存在,而在高分辨率岩心二维图像中,直径小于20 μm的孔隙数目占总孔隙数目的28.23%.因此,只保留高分辨率二维岩心图像中直径小于20 μm的孔隙,并以此作为二维高分辨率训练图像.高分辨率训练图像如图5(a)所示.
同理,根据如图4(b)所示的样本二中低分辨率三维岩心图像二维切片的孔隙分布和高分辨率二维岩心图像的孔隙分布,只保留高分辨率岩心图像中直径小于45 μm的孔隙,并以此作为二维高分辨率训练图像.高分辨率训练图像如图5(b)所示.

(a)样本一高低分辨率岩心孔数目频率对比 (b) 样本二高低分辨率岩心孔数目频率对比
图4 高低分辨率岩心孔数目频率对比
Fig.4 Frequency comparison of pore number of high and low resolution core images

3.1 岩心视觉效果对比
图6(a)为样本一根据本研究提出的算法将2倍低分辨率三维岩心融合重建得到的高分辨率三维岩心图像,图6(b)和图6(c)为融合重建高分辨率岩心以及原始高分辨率三维岩心在相同位置的二维岩心切片图像.

(a) 2倍融合重建高分辨率岩心 (b) 2倍融合重建高分辨率岩心图像 (c) CT扫描高分辨率岩心图像
图6 样本一高分辨率岩心图像
Fig.6 High resolution core image of sample one
图7(a)为样本二根据本研究提出的算法将4倍低分辨率三维岩心融合重建得到的高分辨率三维岩心图像,图7(b)和图7(c)为融合重建高分辨率岩心以及原始高分辨率三维岩心在相同位置的二维岩心切片图像.

(a) 4倍融合重建高分辨率岩心 (b) 4倍融合重建高分辨率岩心图像 (c) CT扫描高分辨率岩心图像
图7 样本二高分辨率岩心图像
Fig.7 High resolution core image of sample two
由图6和图7可知,在低分辨率三维岩心和高分辨率训练图像分辨率相差2倍和4倍的情况下,融合重建的高分辨率三维岩心在三维外观形态和二维外观形态上与真实高分辨率岩心相似,不仅能够较好的重现训练图像中的小尺寸孔隙形态特征及分布,并且可以很好的再现真实高分辨率岩心中的孔隙分布情况.
3.2 岩心孔隙分布对比
岩心孔隙的大小和分布状态对于油层储集与渗流特性有重要影响[17].由于真实岩心孔隙的形状极其不规则,在实际研究中,一般利用孔隙分布的等效球直径来反映孔隙的尺寸大小情况.为了进一步验证算法的准确性和稳定性,我们又在图2(a) 样本一和图2(c) 样本二所示高分辨率岩心图像中分别随机挑取了4张高分辨率二维岩心切片图像,并依照上文所述步骤进行实验.样本一和样本二的真实高分辨率岩心孔隙的等效球直径以及多组融合重建的高分辨率岩心的平均等效球直径分布如图8示.
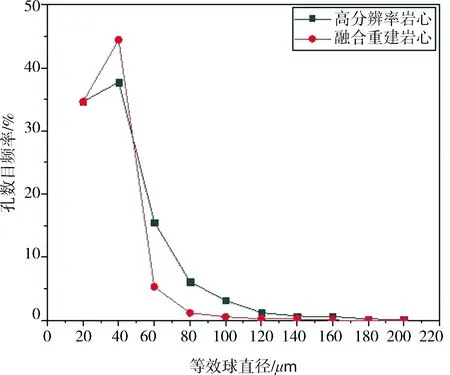
(a)样本一2倍融合重建实验孔隙分布对比 (b) 样本二4倍融合重建实验孔隙分布对比
图8 融合重建高分辨率岩心和真实高分辨率岩心孔隙分布对比图
Fig.8 Comparison of pore distribution between low resolution core images fusion reconstructed high resolution core images and real high resolution core images
如图8所示,样本一在低分辨率三维岩心和高分辨率训练图像分辨率相差2倍的情况下,融合重建岩心和高分辨率岩心在孔数目频率上存在少许误差,样本二在低分辨率三维岩心和高分辨率训练图像分辨率相差4倍的情况下曲线更为接近,误差更小.
3.3 统计特征函数分布对比
多孔介质的微观结构十分复杂,在岩心分析中,一般使用两点相关函数和线性路径函数等作为描述岩心微观结构的重要统计参数[18].在本验证实验中样本一的2倍融合重建高分辨岩心的平均两点相关函数(S2)和平均线性路径函数(L)等特征函数和真实高分辨率岩心的对比如图9.

(a)X方向两点相关函数 (b)Y方向两点相关函数 (c)Z方向两点相关函数

(d)X方向线性路径函数 (e)Y方向线性路径函数 (f)Z方向线性路径函数
图9 样本一统计参数对比
Fig.9 Comparison of statistical parameters of sample one

(a)X方向两点相关函数 (b)Y方向两点相关函数 (e)Y方向线性路径函数
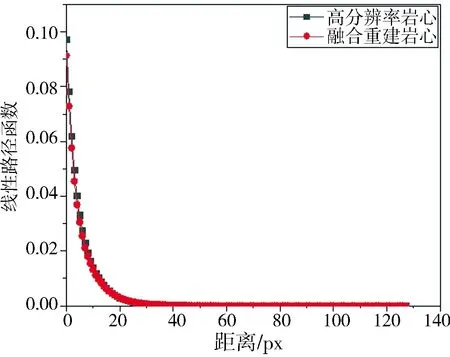
(c)Z方向两点相关函数 (d)X方向线性路径函数 (f)Z方向线性路径函数
图10 样本二统计参数对比
Fig.10 Comparison of statistical parameters of sample two
样本二的4倍融合重建高分辨岩心的平均两点相关函数(S2)和平均线性路径函数(L)等特征函数和真实高分辨率岩心的对比如图10所示.
由图9和图10可知,实验融合重建的高分辨率岩心和真实高分辨率三维岩心的两点相关函数和线性路径函数的分布十分接近.验证了算法的准确性.
由实验及结果分析可以看到,本文提出的基于模拟退火的多尺度岩心融合重建算法可以有效的将高分辨率训练图像的小孔隙信息与低分辨率CT图像进行融合,以重建高分辨率岩心,且融合重建结果有效,准确.
4 结 论
本文借鉴三维重建的思想,提出了一种基于模拟退火的多尺度岩心融合重建算法.为了方便实验的开展和验证算法的有效性,采用下采样的方式来得到低分辨率三维结构,并将去除掉大尺寸孔隙的高分辨率岩心图像的二维切片作为待融合的训练图像,通过模拟退火的方法将训练图像中的小尺寸孔隙融合重建在低分辨率岩心中,以重建高分辨率岩心.通过定量分析以及视觉效果的比较,本算法可以很好的将高分辨率信息融合重建在低分辨率岩心中,验证了算法的有效性.

