多属性直觉模糊容差粗糙集模型

徐伟华 苑克花 李文涛

1西南大学人工智能学院,重庆,400715 2西南大学数学与统计学院,重庆,400715

0 引言

波兰数学家Pawlak所提出的粗糙集理论作为一种数学工具,在处理不确定信息方面有重要作用[1].它主要应用在概念近似与属性约减两个方面[2].概念近似即利用已知的数据,对目标集从上下两个方面对其进行逼近,进而减少目标集的不确定性．经典的概念近似是基于等价关系对分类型数据进行比较刻画[3].由于现实生活中数据的复杂多样化,数据类型还有数值型、区间型、集值型、直觉模糊型等,各对象之间的关系也不仅仅局限于等价关系,所以经典情况下的概念近似有一定的局限性[2-7].

不少学者基于不同数据之间的不同关系进行了很多研究,尤其是对于直觉模糊型数据．直觉模糊型集同时考虑对象对某一集合的正隶属度、负隶属度和犹豫度,具有更强的信息表达能力,能够较好地描述和刻画客观世界的不确定性.文献[8-10]揭示了直觉模糊集理论与粗糙集理论之间的关系,证明每个模糊粗糙集实际上是一个直觉L-模糊集,然后利用直觉模糊集的概念定义了直觉模糊逼近空间中的逼近算子.Liu等[11]通过求解冲突距离来确定对象之间的相似度,进而构建直觉模糊粗糙集模型对研究对象进行刻画.另外,利用区间直觉模糊集和粗糙集相结合的方法,林梦雷等[12]在区间直觉模糊关系的基础上,构造了区间直觉模糊粗糙集模型,主要是利用隶属度与非隶属度求解汉明距离,没有利用犹豫度.本文将进一步结合犹豫度,求解任意两者之间的相似度,并加以乐观悲观思想构建基于容差关系[13]的直觉模糊粗糙集.

本文在直觉模糊信息系统下,结合Jensen等[14]所定义的模糊相似关系,从乐观悲观两个角度出发,提出基于容差关系的直觉模糊粗糙集模型.首先说明构建模型的理论知识,然后构建多属性下乐观、悲观直觉模糊容差粗糙集模型,接着给出实例分析,最后得出结论.

1 预备知识

本节主要介绍了有关直觉模糊系统(IFS)下构建基于容差关系的模糊粗糙集模型的理论基础以及容差关系.

定义1称集合C={〈x,μC(x),νC(x)〉|x∈U}是定义在论域U上的直觉模糊集,其中:μC(x)表示x对集合C的隶属度;νC(x)表示x对集合C的非隶属度;同时0≤μC(x)+νC(x)≤1,πC(x)=1-

μC(x)-νC(x)表示x对集合C的犹豫度,显然πC(x)∈[0,1].有序对〈μC(x),νC(x)〉是x在集合C下的直觉模糊值.

定义2称I=(U,C,IF,V)为直觉模糊信息系统,其中:U={x1,x2,…,xn}是非空有限论域;C={c1,c2,…,cm}是非空有限条件属性集;IF:U×C→V是U与C的关系集,并且V(x,c)=〈μc(x),νc(x)〉,(∀x∈U,c∈C);V是不同对象在不同属性下取值所构成的值域.

为了衡量同一个直觉模糊集合下不同对象之间的相似度,依据文献[13]选取定义3的相似度函数.

定义3称Sc(xi,xj)为定义在属性c下xi与xj的相似度[13],具体定义如下:

Sc(xi,xj)=1-(α(μc(xi)-μc(xj))2+

β(νc(xi)-νc(xj))2+γ(πc(xi)-πc(xj))2)1/2,

其中:

1)α≥β>γ;

2)α+β+γ=1;

3)0≤α,β,γ≤1．

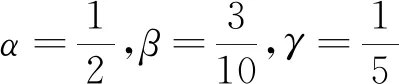
定义4设S=Sc(xi,xj)∈μn×n,其中μn×n表示维度为n×n的模糊矩阵的全体.对于任意的λ∈[0,1],称Sλ=(sc(i,j)λ)为模糊矩阵S=Sc(xi,xj)的λ-截距阵,其中:

显然,λ-截距阵Sλ为布尔矩阵.

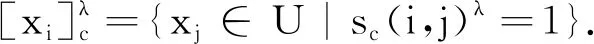
定义5设U={x1,x2,…,xn}是所研究对象的全体,C={c1,c2,…,cm}是条件属性集合,X⊆U是目标集．给定λ的具体取值以及属性c∈C,结合粗糙集[1]定义,可知在属性c下有关目标集X的上下近似定义如下:

其中Ø代表空集,表示两个集合没有公共元素.

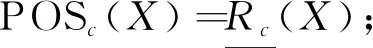
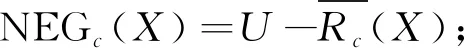
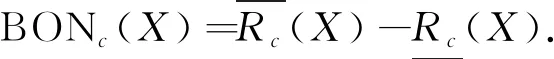
定义6[2]在直觉模糊信息系统I=(U,C,IF,V)下,给定目标集X,以及属性子集A⊆C,则属性集A下X的近似精度α(A,X)定义为

2 多属性下直觉模糊容差粗糙集模型

由定义5可以求出直觉模糊信息系统中,某一具体属性下目标集的上下近似.但是,现实生活中某一对象往往有多个属性,针对这种情况我们提出乐观直觉模糊容差粗糙集模型与悲观直觉模糊容差粗糙集模型.

设U={x1,x2,…,xn}是论域,C={c1,c2,…,cm}是条件属性集合,X⊆U是目标集,给定λ的具体取值.

在条件属性集C中,有关目标集X的乐观上下近似定义如下:

“∨”表示“或”,“∧”表示“且”.

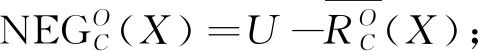
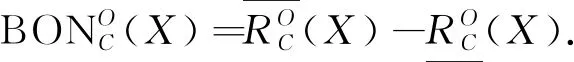
在条件属性集C中,有关目标集X的悲观上下近似定义如下:

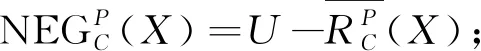
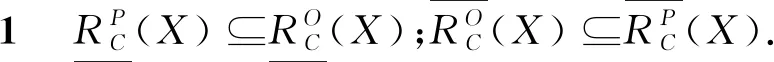
证明根据目标集X乐观与悲观的上下近似定义可直接推导.

根据定义6中近似精度定义可知:在直觉模糊信息系统I=(U,C,IF,V)下,给定目标集X,以及属性集C,则属性集C下X的乐观近似精度αO(C,X)定义为

相应的悲观近似精度αP(C,X)可类似定义.

3 实例分析

针对本文所提出的多属性下直觉模糊容差粗糙集模型,为了进一步验证其性质,我们给出一个具体的实例,通过求解目标集的乐观,悲观上下近似来验证直觉模糊容差粗糙集模型其性质.

给定一个直觉模糊信息系统I=(U,C,IF,V)(表1),其中:论域U={x1,x2,…,x6},条件属性集C={c1,c2,…,c6},目标集X={x2,x3,x4}.

表1 直觉模糊信息系统

各个属性下的相似度矩阵S1，S2，S3，S4分别为

根据相似度矩阵我们可以得到四个属性下的相似类分别是:

根据上下近似定义可知,目标集X的乐观悲观上下近似如下:

根据计算结果,可知:

4 结论

本文在直觉模糊信息系统中提出一种新的多属性下直觉模糊粗糙集模型.首先,利用相似度函数,通过求解不同对象之间对某一集合的隶属度,非隶属度以及犹豫度之间的差值,求出相似度矩阵;然后,根据相似度矩阵求出不同属性下各个对象的相似类;最后,根据本文所定义的乐观悲观上下近似,从上下两个角度对目标集进行刻画.另外,通过求解可以发现直觉模糊信息系统下,乐观近似精度在数值上大于悲观近似精度.在接下来的工作中,我们可以考虑直觉模糊信息系统下,从乐观悲观两个角度进行属性约减,进而减少计算时间,节约内存.