基于饱和约束和时变观测器设计的异构航天器姿态控制策略

王博辉

1西安电子科技大学空间科学与技术学院,西安,710071

0 引言

随着载人航天技术的不断成熟,未来太空运输中将会出现多种类型的载人航天器．特别是随着太空资源的不断开发,利用有限的异构航天器资源对未知目标进行合作探测与识别具有重要意义．基于此,合作控制作为空间信息物理系统的主要技术,近年来受到了广泛关注[1-3]．例如典型的技术包括机器人合作控制、合作机器学习算法、分布式任务优化、智能交通等．值得指出的是,合作控制能够利用有限的通信资源和原材料供应降低能源的消耗和生产成本．基于此,不同类型的合作控制协议被开发来获得更多的合作利益．由于在实际的工程应用中,系统通常包含非线性和不确定性,特别是包含异构组件或者参数,因此面向异构系统的合作控制技术具有更优的可靠性和实用性．

实际上,对于异构系统而言,主要的挑战是闭环系统不存在共同的平衡点,因此其系统的稳定性分析显著地不同于同质系统的稳定性,因而其问题研究也更具挑战．传统的异质系统合作控制主要有两类方法．一种是准同步分析方法,它强调异质系统在合作控制时会存在一个有界的同步误差等级,典型的工作包括同步分析[4]、分布式脉冲同步[5]、部分一致性分析[6]、混杂系统准一致性[7]等．然而,由于有界的误差等级在估计时依赖一个较强的假设,即所有追踪者都需要与领导者存在一条直接相关联的链路．这种分析对于大规模复杂互连系统是有效的．然而,对于异质系统仅存在有限资源可以调度的场景下,分布式合作一致性很难实现．另外一种方法是合作输出调节,它拓展传统的输出调节从单一对象到多个体系统．假设一部分个体能够获得领导者的系统矩阵,该方法进而被拓展到合作自适应输出调节问题[8]．然而,合作输出调节依然需要领导者的系统矩阵是完全或者部分个体可知的,这直接关系到调节方程的可解性．在一些实际应用中,如果领导者的系统矩阵是完全未知的,例如外系统动态变化的频率是未知的,但是其信号可以通过有限的设备被估计或者探测到．在这种情况下,如何实现完全一致性行为更具挑战．

本文关注异质系统存在输入饱和约束和不确定性动态的鲁棒一致性追踪问题．由于执行器的能力限制,输入饱和是一种常见的非线性行为．如果忽视饱和的影响,系统的性能会退化甚至导致系统变得不稳定．对于输入饱和约束,一个典型的方法是低增益反馈控制,它通过一系列参数化的镇定反馈增益来实现半全局镇定．当参数趋于零时,反馈增益将趋于零．典型的实现方法包括特征根配置、参数 ARE (Algebraic Riccati Equation) 方法,以及参数Lyapunov 方法.然而,对于含有非线性和不确定动态的异质系统,当设计参数趋于零时,反馈增益趋于零会导致系统变得不稳定．为了解决该问题,一种变异的低增益饱和控制方法[9]被提出．因此不同于已有的工作,本文的贡献包括三个方面．第一,本文考虑在异质系统的合作控制中,领导者的系统矩阵是完全未知的．为了解决这个问题,本文提出了两类系统动态:第一种是分布式观测器动态,它主要利用邻居信息对领导者的状态进行估计;第二种是追踪动态,它主要实现个体对其观测信号的追踪一致性．我们的目的是实现这两种动态的同步收敛．显然,这种设计可以拓展准同步分析应用于分布式协调控制．特别地,我们仅仅要求通信拓扑包含有向生成树,它可以拓展准同步中要求的全连通条件．第二,本文提出的双重同步框架,其分布式观测并不依赖领导者系统矩阵．通过提出适当的估计动态,我们能够拓展输出调节方法应用于领导者系统矩阵完全未知的情形．第三,本文关注的异质系统合作控制考虑输入饱和约束．由于存在非线性和不确定性动态,我们并不要求控制器的增益会无穷趋于零．通过利用变异的低增益饱和控制方法,我们能够提高合作系统的鲁棒性,使其方法在异构航天器姿态控制中具有更好的控制性能．

本文的结构如下:第一章介绍异构航天器的姿态控制模型．第二章介绍异构航天器的姿态控制策略,这也是本文的主要工作．第三章通过一个仿真例子来验证所提方法的有效性．最后,第四章给出本文的结论．

1 异构航天器的姿态控制模型

异构航天器的姿态矩阵、姿态运动学和动力学可以描述为如下动态方程:

[hi,x,hi,y,hi,z],

(1)

(2)

(3)

(4)

其中σi,1=(Ji,2-Ji,3)/Ji,1,σi,2=(Ji,1-Ji,3)/Ji,2,σi,3=(Ji,2-Ji,1)/Ji,3．进一步地,考虑俯仰角系统含有非线性动态和模型不确定性,则航天器的状态空间方程可以描述为

Xi=(Ai+ΔAi)Xi+Cifi(Xi)+Bisat(Ui),

(5)

2 异构航天器的姿态控制策略

基于上文分析,异构航天器的飞行动态可以描述为异质系统的状态空间方程．因此,接下来将围绕异质系统的鲁棒一致性追踪控制问题展开论述．由于异质动态会引起系统平衡点的差异,特别地,我们考虑异质航天器的动态能够利用有限的资源实时的对未知目标的状态信息进行观测与估计．基于此信息,我们将提出异质动态补偿协议来实现异质系统的稳定性．假设一组异质系统包含N个个体,并且个体的动态能够描述为

(6)

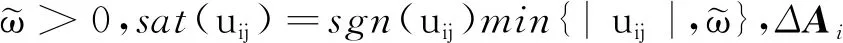
此外,领导者系统(外系统)可以表示如下:

(7)

其中ξ0∈Rn是领导者系统的状态,f0(ξ0)是领导者系统的非线性动态,A0和C0是两个未知的系统矩阵．

注1由于本文考虑领导者的系统矩阵是完全未知的,因此领导者的系统动态并不能实时地被所有追踪者获得．我们考虑在实际应用中可以利用有限的设备对某个未知目标的状态进行观测,因此我们假设目标系统的动态并不是完全可知,但是其运动位置可以被有限的个体观测到．这种情况是实际存在的,例如外系统的动态不能被预测,但是其位置可以利用有限的手段获取到．这些考虑使得鲁棒一致性追踪问题更加实际,因此也更难被解决．

为了引入的解决方案,首先对系统进行如下假设:

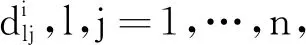
x,y∈Rn.

(8)

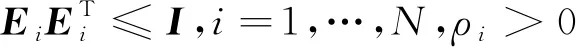
我们的目标是设计一个新的鲁棒一致性追踪算法使得所有异质的追随者能够达到领导者的位置．该问题可以描述如下:

定义1异质系统(6)和(7)达到鲁棒一致性追踪当且仅当我们可以合理地设计协调控制器ui来确保所有个体的状态接近领导者的状态,例如:

(9)

其中ξ0是领导者的状态,xi(0)∈χ,χ∈R是已知的集合．

注2本文考虑异质非线性个体动态,因此合作系统并不存在共同平衡点．为了解决这个问题,我们首先设计一个分布式观测器来补偿平衡点的误差动态．由于领导者的动态是完全未知的,我们仅仅能够估计领导者的状态信息,但是并不知其动态演化过程．因此,如何获得异质合作系统的稳定解,并且确保鲁棒一致性追踪能够被获得将是本文的研究重点．

为了补偿异质系统的平衡点误差,首先提出一个新的分布式观测器协议来估计领导者的状态:

gi(ξ0-ξi))+Cif0(ξi),

(10)

其中ξi∈Rn代表分布式观测器状态,α>0是耦合强度,γ是一个标量,Fi(γ)∈Rn×n是观测器增益,gi≥0是牵制增益,gi>0意味着个体能够获取领导者的信息．进一步地,定义G=diag(gi)∈RN×N．

为了获得我们的结论,我们同时引入如下假设和引理:

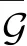
由于领导者的系统矩阵并不可知,因此引入如下平均观测器状态作为目标信号:

(11)

(12)

(13)

我的房间里堆着许多铲子，新的旧的生锈的，我妈说，看到它们，就会想到我。每想我一次，就会去买一把铲子，不知不觉就堆满了房间。

为了获得鲁棒一致性追踪控制,我们设计如下综合了分布式观测和一致性协议的控制器:

(14)

其中Ki(γ)是反馈增益,Bi是权重矩阵．

Cif0(ξi)=(Ai+ΔAi)εi+Cifi(xi)+ui+

Cifi(xi)-Cifi(ξi)-BiKi(γ)εi+

(15)

因此,追踪误差动态可以记为

(16)

因此,我们可以给出如下定理:

定理1异质系统(6)和(7)获得鲁棒一致性追踪的条件为

1)假设1—3满足;

2)下面的方程有可行解:

(17)

(18)

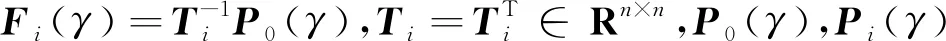
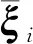
(19)

和

首先考虑输入饱和约束对异质系统鲁棒一致性追踪的影响,令c1>0和c2>0为常量,且满足:

(20)

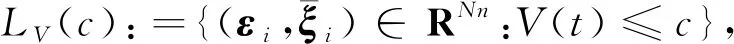
(21)

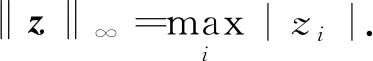
G)TΘ(L+G))⊗IN)(Θ-1⊗IN)×

(22)

利用柯西不等式,可以得到:

(23)

进一步地,选择耦合强度满足条件α>ω/λ0,其中λ0=λmin(Θ(L+G)+(L+G)TΘ),Θ={1/θ1,…,1/θN}．则

G)TΘ(L+G))⊗IN)(Θ-1⊗IN)×

G)TΘ(L+G))⊗IN)(Θ-1⊗IN)×

G)TΘ(L+G))⊗IN)(Θ-1⊗IN)×

G)TΘ(L+G))⊗IN)(Θ-1⊗IN)×

(24)

(25)

2Pi-1(γ)BiKi(γ))εi+

(26)

(27)

利用柯西不等式,可得:

(28)

(29)

(30)

综上所述,利用条件(19),(25)和(30)可得：

(31)

3 仿真结果与性能比较

本文考虑7个异构航天器的鲁棒一致性追踪问题,其中异构参数主要包括惯性矩阵、高度等参数．为了确保方法的有效验证,所选取的异构的参数都来自于文献[10-12]．

3.1 异构航天器的鲁棒一致性追踪

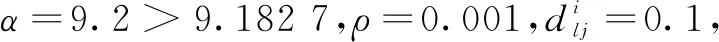
3.2 不同参数下的异构航天器姿态控制性能分析

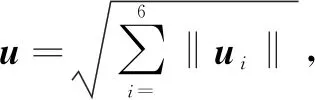
为了对比不同参数下的控制性能,我们引入了均值、标准差和方差3个指标．其性能分析如图3所示．

通过图3可知,当增益参数趋于零时,观测器输入和控制器的均值、方差和标准差都将逐渐减少．较小的控制器增益,其同步追踪误差的均值、方差和标准差也将适当地增加,这是由于饱和约束引起的性能损失．也就是说,当执行器存在输入饱和时,异构系统的姿态控制收敛速度依赖增益参数的设计．当增益参数减少时,饱和现象将不会存在执行器,这是以牺牲控制性能为代价的．

4 结束语

本文针对实际空间环境中异构航天器存在强非线性和不确定性等影响,以及考虑执行器存在输入饱和约束等问题,提出了面向异构航天器包含饱和输入和不确定性动态的鲁棒一致性追踪控制策略．该控制策略允许目标系统的动态权重矩阵是完全未知的．通过提出新的权重矩阵平均观测器动态,设计了一类新的鲁棒一致性追踪控制器．该控制策略综合了分布式观测和一致性追踪协议,能够在保证追踪性能的同时提高控制策略的鲁棒性．仿真结果表明,利用不同的低增益参数,输入饱和现象被解决,并且异构航天器的姿态控制性能得到了保证．分析表明,提出的控制策略基于分布式参数,具有较强的灵活性,易于工程实现．