C型独立舱液货罐热分析

石玉美，沈菊华，邹荡平，秦天怡

（1. 上海交通大学 机械与动力工程学院，上海 200240；2. 上海铠韧气体工程股份有限公司，上海 200441）

0 引 言

近年来，随着经济的不断发展，加上污染物排放法规日益严格，液化天然气（Liquefied Natural Gas,LNG）、乙烯和乙烷等清洁能源及化工原料的需求与日俱增。这些气体在常压下的饱和温度均较低，一般采用全冷式或半冷半压式运输方式来运输。

在采用半冷半压式运输方式过程中，货物通常采用独立C型罐储运。独立C型罐能承受一定的压力，可根据容积的大小设计成单体罐、双体罐和三体罐。独立C型罐一般采用5Ni钢或9Ni钢建造，无需设置次屏蔽层，船型结构相对简单；罐体与船体可同时施工，建造完成之后统一吊装，能大大缩短建造周期，从而降低建造成本。因此，中小型液化气船普遍采用独立C型罐[1-3]。

罐内货物的温度通常较低，与罐外环境存在较大的温差。虽然罐体通常会采取绝热措施，但罐内的货物仍会因漏热而蒸发。文献[3]对独立C型罐进行了定性热分析，而对其进行定量热分析也很重要，这是由于，为避免储罐内的货物超压排放，需计算其蒸发量，并据此设计合适的再液化装置。

本文以32000m3半冷半压式液化气船1号液货罐为研究对象（见图1），以装载乙烯为例进行热分析，计算中除了管道以外，其他装置均采用ANSYS建模[4-5]。

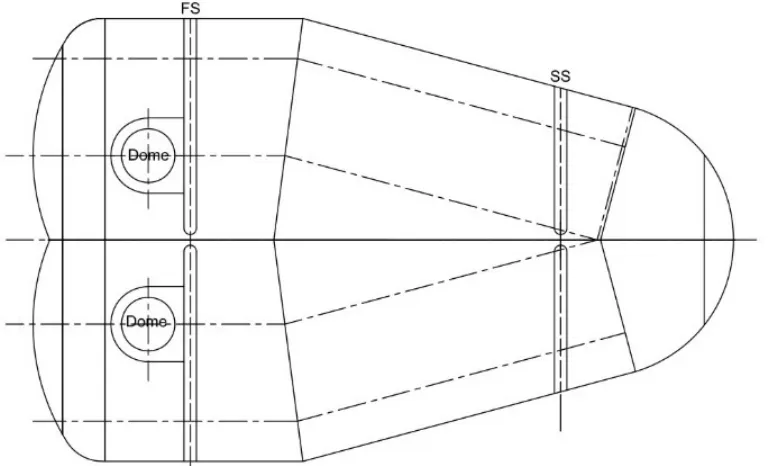
图1 32 000 m3半冷半压式液化气船1号液货罐

1 计算内容和计算方法

该液化气船装载的液货为乙烯，在大气压下的饱和温度为169.06K，液相密度为567.1kg/m3，潜热为476.21kJ/kg。

本文对该船1号罐装载乙烯时的漏热量进行计算，漏热量包括通过液货罐筒体、液货罐封头、固定端鞍座、滑动端鞍座、止浮装置、气室和管路的漏热量。对于通过液货罐筒体、液货罐封头、固定端鞍座、滑动端鞍座、止浮装置和气室的漏热量，通过采用有限元计算软件ANSYS12.1建立有限元模型来计算；对于通过管路的漏热量，采用导热公式来计算。得到各部分的漏热量之后，计算液货罐的总漏热量和液货的蒸发量，进而计算得到液货罐的蒸发率。

2 材料属性

在漏热量计算中，涉及到的材料有：

1) 5Ni钢，用作罐体、止浮装置和气室组件；

2) 60kg/m3的绝热层，用作罐体及相关组件的内层绝热；

3) 40kg/m3的绝热层，用作罐体及相关组件的外层绝热；

4) 硬木，用作鞍座和止浮装置中的一些组件，导热系数为0.21W/(m·K)；

5) 胶，用于粘接硬木和钢材，导热系数为0.684W/(m·K)；

6) 316L，用作气室中的接管材料，在100K温度下的导热系数为15.1W/(m·K)，在300K温度下的导热系数为 18.4W/(m·K)。

表1为5Ni钢和2种绝热层材料的导热系数。

表1 5Ni钢和2种绝热层材料的导热系数

3 热边界条件

液货罐内的压力为标准大气压1.01325×105Pa，罐内的温度为对应的液货在大气压下的饱和温度。液货罐外最高海水温度为305.15K，最高环境温度为318.15K。在计算中，甲板以上的罐体及相关组件外壁的温度取318.15K，甲板以下的罐体及相关组件外壁的温度取最高海水温度与最高环境温度的平均值311.65K。外表面与空气的自然对流换热系数取5W/(m2·K)。

由于罐体对称，下面所述漏热量为图1所示液货罐的1/2罐体的漏热量。

4 漏热分析

下面对通过液货罐筒体、液货罐封头、固定端鞍座、滑动端鞍座、止浮装置、气室和管路的漏热量进行计算，给出采用ANSYS计算得到的漏热量和温度分布图，其中温度的单位为K。

4.1 通过液货罐筒体的漏热量

在计算通过液货罐筒体的漏热量时，先计算单位面积的漏热量，再计算总面积下的漏热量。筒体绝热层由罐体外50mm厚的60kg/m3绝热层和150mm厚的40kg/m3绝热层组成。

采用ANSYS建模计算，建模时筒体长度方向取1m，周向取5°。得出漏热量之后，先将其除以ANSYS模型中5Ni钢外表面对应的面积，得到单位面积的漏热量，再将该漏热量乘以1号液货罐1/2筒体对应的5Ni钢外表面面积，即可得到筒体的漏热量。

图2为采用ANSYS计算得到的液货罐筒体温度分布图。采用ANSYS计算得到的漏热量为8.93W，模型对应5Ni钢外表面的面积为0.668 m2，则单位面积的漏热量为13.368 W/m2；筒体的面积为869.5 m2，则筒体的漏热量为11623.8 W。

4.2 通过液货罐封头的漏热量

1号液货罐后封头由半径为12.24m的部分球体和半径为2.356m的部分球体组成；1号液货罐前封头由半径为7.655m的部分球体组成。

在采用ANSYS建模时，建立1°球体的模型。图3为采用半径为2.356m的球体计算得到的液货罐封头温度分布图。

图2 液货罐筒体温度分布图

图3 液货罐封头温度分布图

通过建模计算得到的1号液货罐前封头和后封头的漏热量见表2。

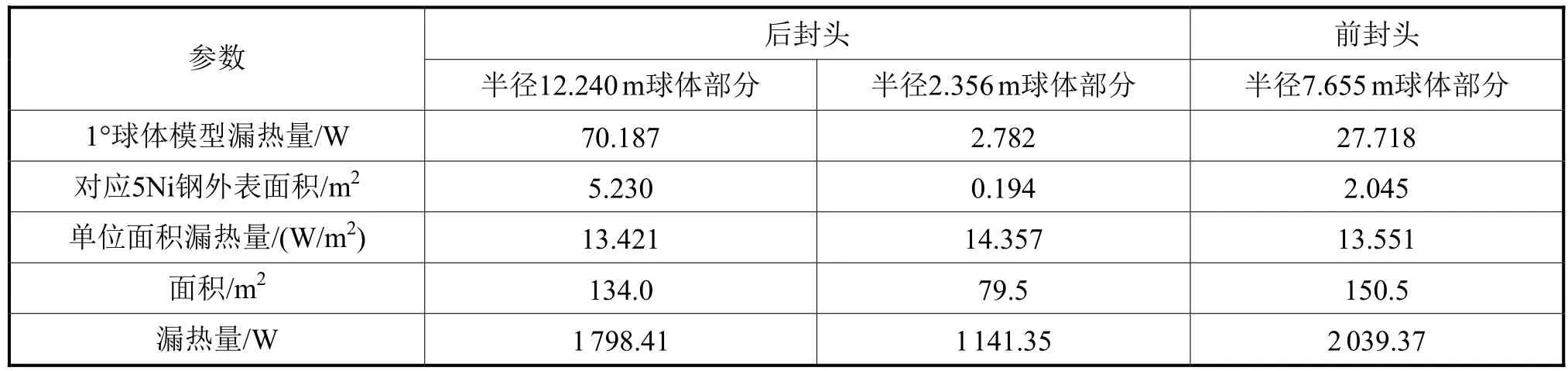
表2 1号液货罐前封头和后封头的漏热量

4.3 通过固定端鞍座的漏热量

固定端鞍座的弧度为110°。鞍座两侧的绝热结构与筒体不同，在计算中分别对固定端鞍座及一侧的不规则绝热层进行建模。建模时，建立弧度为1°的模型，乘以总弧度110°，即可得到总漏热量。

图4为采用固定端鞍座弧度为1°的ANSYS模型计算得到的固定端鞍座温度分布图。采用ANSYS模型计算得到的漏热量为21.676W，整个固定端鞍座的漏热量为2384.390W。

图5为采用固定端鞍座一侧不规则绝热层弧度为1°的ANSYS模型计算得到的固定端鞍座一侧绝热层温度分布图。采用 ANSYS模型计算得到的漏热量为 3.156W，整个固定端鞍座两侧不规则绝热层的漏热量为694.35W。

图4 固定端鞍座温度分布图

图5 固定端鞍座一侧绝热层温度分布图

4.4 通过滑动端鞍座的漏热量

滑动端鞍座的弧度为 81°。计算中取 1/2滑动端鞍座及一侧的不规则绝热层建模。建模时，建立弧度为1°的模型，先乘以总弧度81°，再乘以2，即可得到滑动端鞍座及两侧不规则绝热层的总漏热量。

图6为采用弧度为1°的ANSYS模型计算得到的1/2滑动端鞍座及一侧绝热层温度分布图。采用ANSYS模型计算得到的漏热量为7.417W，滑动端鞍座总漏热量为1201.590W。

4.5 通过止浮装置的漏热量

图7为采用止浮装置的ANSYS模型计算得到的止浮装置温度分布图。采用ANSYS模型计算得到的1个止浮装置的漏热量为239.684W，2个止浮装置的漏热量为479.367W。

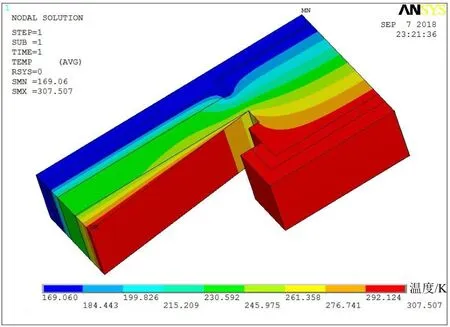
图6 1/2滑动端鞍座及一侧绝热层温度分布图

图7 止浮装置温度分布图

4.6 通过气室的漏热量

对通过气室的漏热量进行计算，建模时圆周方向取5°。图8为采用气室的ANSYS模型计算得到的气室温度分布图。采用ANSYS模型计算得到的漏热量为6.907W，整个气室的漏热量为497.300W。

4.7 通过管路及气室支撑的漏热量

在液货罐中，通过管路及气室支撑的总漏热量为257.9W。

4.8 1号液货罐总漏热量和静态日蒸发率

由第4.1～4.7节的计算分析得到通过罐体、固定端鞍座、滑动端鞍座、止浮装置、气室和管路的漏热量，汇总数据见表3，其中罐体漏热量包括液货罐筒体的漏热量和前后封头的漏热。

图8 气室温度分布图

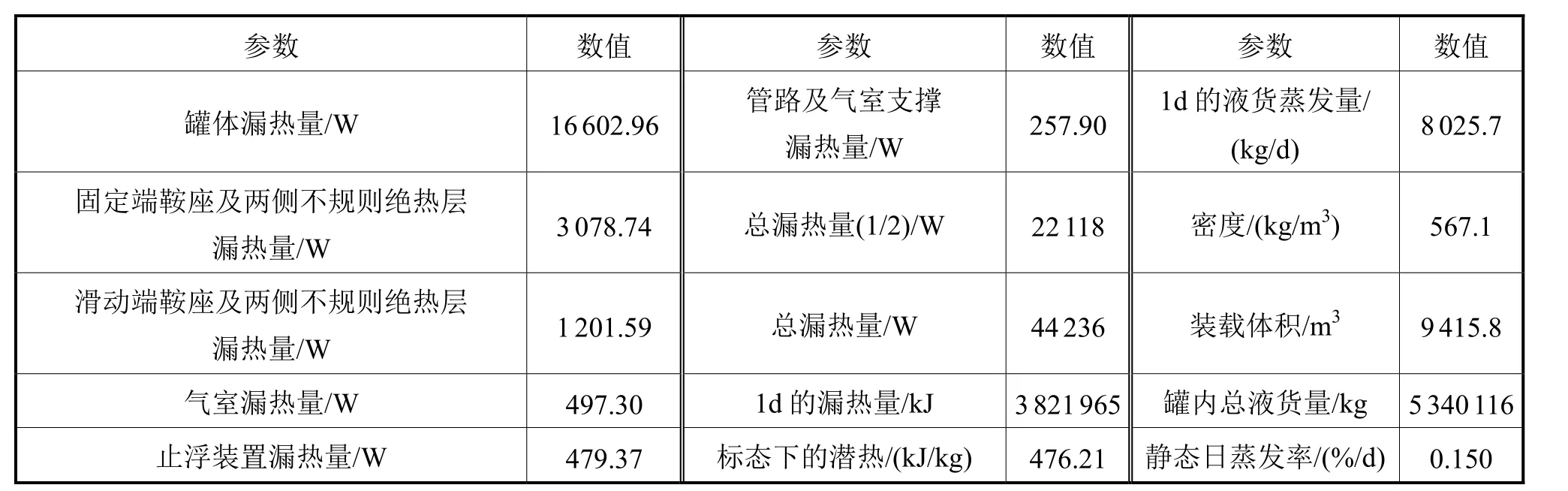
表3 1号液货罐的漏热量、液货蒸发量、蒸发率

从表3中可看出：罐体漏热量占液货罐总漏热量的75.1%，通过鞍座及两侧不规则绝热层的漏热量占19.4%，其他部分的漏热量占比均较小。

5 结 语

本文对32000m3液化气船C型独立舱中的1号液货罐进行了热分析，对通过1号液货罐的筒体、封头、固定端鞍座、滑动端鞍座、止浮装置、气室和管路的漏热量进行了计算，得到了1号液货罐的漏热量为44.24kW，1d的液货蒸发量为8025.7kg，蒸发率为0.15%/d。在各漏热环节中，罐体漏热量所占比例最大（为75.1%）；其次为通过鞍座及两侧不规则绝热层的漏热量（为19.4%），其他部分的漏热量占比均较小。