基于Dynamo的热力管道绝热层经济厚度计算

赵霄强

（上海市政工程设计研究总院集团第十市政设计院有限公司，甘肃 兰州 730000）

1 引言

目前，工程中管道绝热层经济厚度通常通过查表、查图确定，然而工程图表是在一定的外部条件下编制的，工程人员在应用时必须注意其相应的适用条件，当不满足适用条件时，必须按照标准要求重新计算[1]。同时，性能优良的新型保温材料不断涌现[2]，并得到应用[3-4]，需要对绝热层经济厚度进行重新核定[5]。然而，按照规范要求手工计算管道绝热层经济厚度困难较大，利用有限元软件对管道传热进行分析的流程相对复杂[6]。

Dynamo是一款基于Revit的计算机辅助设计工具，该工具具有强大的列表处理功能。本研究利用Dynamo对管道绝热层经济厚度进行计算，将计算结果与图集表格进行对比，并对绝热层经济厚度的影响因素进行分析。

2 管道绝热层经济厚度的计算方法

根据规范要求，圆形管道绝热层经济厚度可按式（1）进行计算[7]。

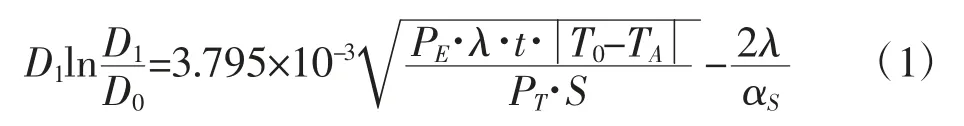
式中：D1为绝热层外径，m；D0为管道外径，m；PE为能量价格，元/GJ；λ为绝热材料在平均温度下的导热系数，W/（m·℃）；T0为管道外表面温度，℃；Ta为环境温度，℃；PT为绝热层单位造价，元/m3；S为绝热工程投资年摊销率，%；αs为绝热层外表面放热系数，W/（m2·℃）。

图集中给出的绝热材料导热系数可以简化为式（2）的形式[8]，通常与保温材料厂家提供的材料导热系数线性回归公式相一致。

式中：Tm为绝热层内、外表面温度的算术平均值，℃；a、b为常量，根据绝热材料种类和使用温度确定。其中，Tm可根据式（3）计算。

式中：TS为绝热层外表面温度，℃。

绝热层外表面放热系数αS按照式（4）进行计算。

式中：αr为绝热层外表面材料辐射换热系数，W/（m2·℃）；αc绝热层外表面对流换热系数，W/（m2·℃）。

αr可按式（5）计算，见式（5）：

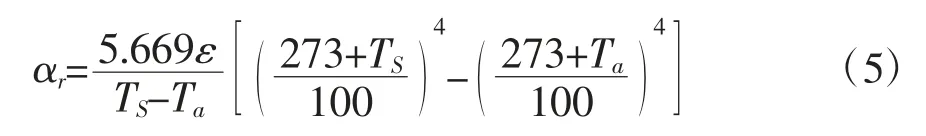
绝热层外表面对流换热系数αc与室外年平均风速W相关，当WD1≤0.8 m2/s时，αc按式（6）计算。

当WD1＞0.8 m2/s时，αc按式（7）计算。

式（1）为隐函数形式，无法直接求解；导热系数、外表面换热系数与绝热层外表面温度存在函数关系，更增加了求解的难度。在管道绝热层经济厚度的计算中需要大量迭代，手工计算几乎无法完成。

3 利用Dymamo计算绝热层经济厚度的思路

Dynamo是一款可视化编程软件，其对列表有强大的编辑、处理能力[9]，本研究正是利用该软件的列表处理能力来解决绝热层经济厚度计算的问题。

在管道稳态传热条件下，通过绝热层的热流量和通过表面传热的热流量相等[10]，即满足式（8）要求。

当环境温度、风速一定时，式（8）存在无穷组解，给定一个绝热层外径D1，即可求出一组解{D1，λ，αS，TS，Φ...}。在无穷组解中，存在一组解使式（1）左右两侧差值的绝对值最小，该组解所对应的D1即为管道绝热层经济厚度下的绝热层外径，从而可求出绝热层经济厚度。为了控制式（8）的解的数量，需要对绝热层外径D1、绝热层外径梯度ΔD1、绝热层外表面温度的最大值TSmax、绝热层外表面温度梯度ΔTS作出一定限制。

3.1 绝热层外径列表LD1

在工程中，管道绝热层外径并不是无穷大的，为了减少绝热层外径列表容量，需要给定其上限D1max，D1max=A×D0（A>1）。在给定A值情况下，当式（1）两侧差值的绝对值的最小值对应的序号加1小于列表项数时，则式（1）存在解，即设定的最大绝热层外径D1max大于绝热层经济外径；否则，式（1）不存在解，即设定的D1max小于绝热层经济外径，此时要增大A值，直至式（1）存在解。

绝热层外径梯度ΔD1对LD1的容量影响很大，ΔD1越小，列表容量越大，计算出的结果越精确，通常当ΔD1=1 mm时，即可满足工程计算要求。

通过以上分析，对于φ27的管道（DN20），当A=2时，ΔD1=1 mm时，最终形成的列表为{28、29、30...52、53、54}mm，如图1所示。

图1 绝热层外径列表LD1

3.2 绝热层外表面温度列表LTS

在管道采取保温措施后，TS通常会小于防烫伤温度，为了减少LTS容量，需要给定其上限TSmax（T0>TSmax>Ta）。

同时，绝热层外表面温度梯度ΔTS对LTS容量的影响也很大，ΔTS越小，列表容量越大，计算出的结果越精确，通常当ΔTS=1 ℃时，即可满足工程计算要求。

通过上述分析，当T0=80 ℃，TSmax=65 ℃，Ta=20 ℃，ΔTS=1 ℃时，最终形成的列表为{64、63、62...23、22、21}mm，如图2所示。

图2 绝热层外表面温度列表LTS

3.3 保温层导热系数列表Lλ

在已知T0及LTS时，根据式（2）可计算出Lλ，如图3所示。

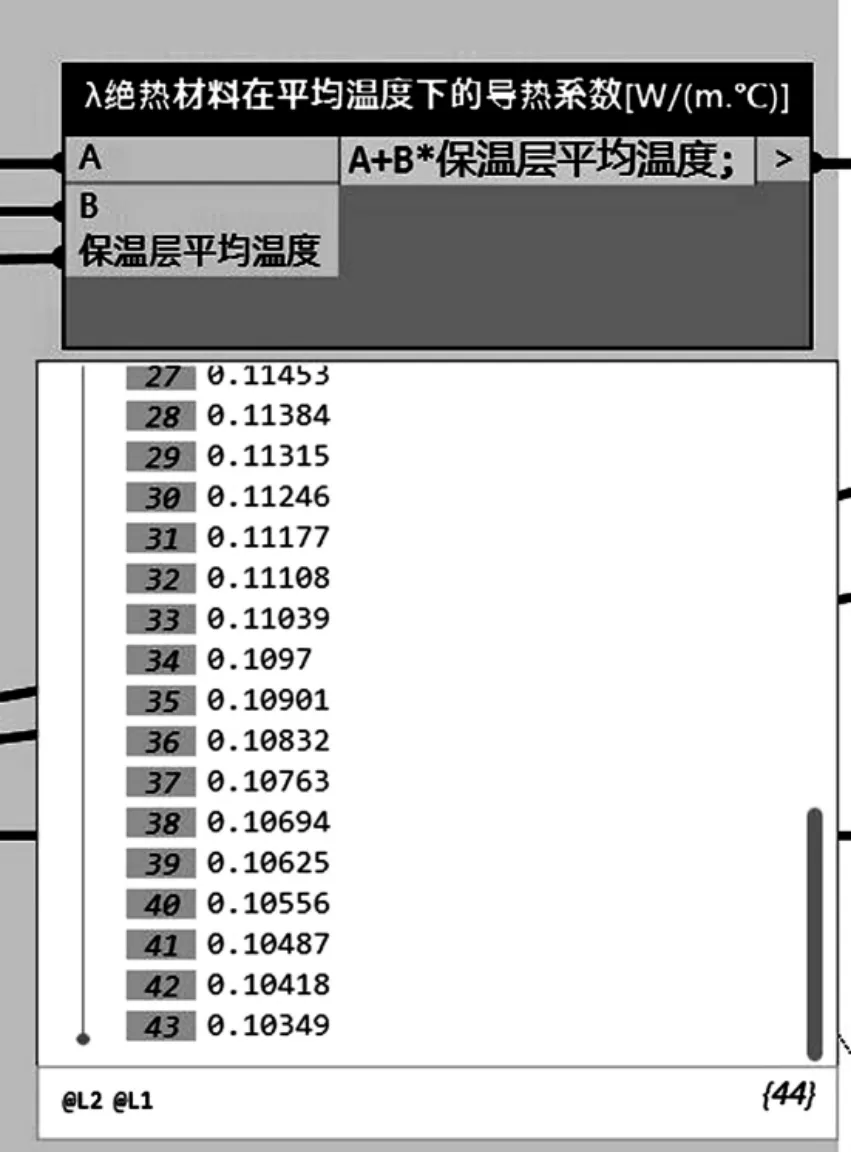
图3 保温层导热系数列表Lλ

3.4 绝热层外表面换热系数列表LαS

在已知年平均风速W、绝热材料外表面绝热黑度ε、Ta下，并结合Lλ、LTS，根据式（4）可计算出LαS，如图4所示。需要注意的是LαS为二维列表，其他列表为一维列表，根据式（8）计算热流量时，需要将列表转换为相同的维度。

图4 绝热层外表面换热系数列表LαS

3.5 热流量列表Lφ1、Lφ2

在已知LTS、Lλ、LD1、D0、T0时，由式（8）可计算出通过绝热层外表面因为导热而产生的热流量列表Lφ1；在已知LαS、LTS、T0、LD1时，由式（8）可计算出通过绝热层外表面因为对流、辐射而产生的热流量列表Lφ2。Lφ1与Lφ2差值的绝对值最小时（如图5所示），所对应的温度，即为在一定绝热层外径D1下的绝热层外表面温度TS。

图5 Lφ1与Lφ2差值的绝对值

以上是求管道传热的通用过程，Dynamo可将以上过程封装为一个节点，可简化程序，并增强程序的可读性，如图6所示。

图6 封装节点

3.6 求解绝热层经济厚度下的绝热层外径

在已知PE、t、PT、S、D0时，将以上列表带入式（1），满足等式两侧差值最小时的D1即为绝热层经济厚度下的绝热层外径，进而可求出绝热层经济厚度。

4 程序计算结果与图集的对比

为了验证程序的正确性，本研究分别以闭孔橡塑泡沫绝热层和硅酸铝棉绝热层为例，计算在不同热价、不同介质温度、不同运行时间下的绝热层经济厚度，并与图集进行对比，如图7—图8所示。

图7 闭孔橡塑泡沫绝热层在不同热价、介质温度、运行时间时程序计算值与图集值的对比

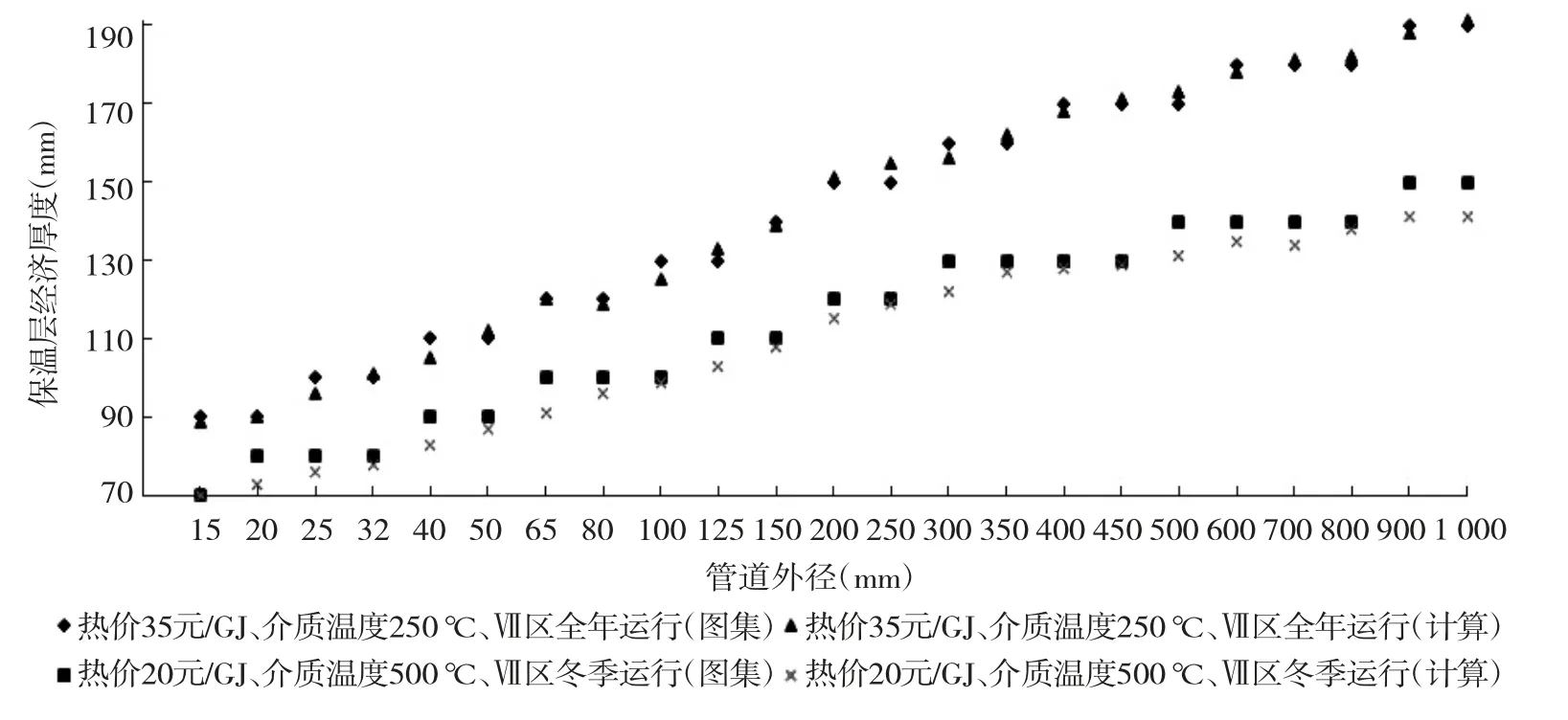
图8 硅酸铝棉绝热层在不同热价、介质温度、运行时间时程序计算值与图集值的对比

图集中给出了计算绝热层厚度的圆整规则，闭孔橡塑泡沫绝热层和硅酸铝棉绝热层的厚度档次划分，见表1。

表1 闭孔橡塑泡沫绝热层和硅酸铝棉绝热层的厚度档次划分 单位：mm

其中，闭孔橡塑泡沫绝热层δ最小厚度为16 mm，当δ≤28 mm时，以3 mm为一档；当28 mm<δ≤40 mm时，以4 mm为一档；当δ>40 mm时，以5 mm为一档。硅酸铝棉绝热层厚度δ最小厚度为20 mm，以10 mm为一档。

由图7可以看出，绝热层厚度区间内，程序计算结果与图集值的差值Δδ≤2 mm，小于各区间的最大档次值3 mm。

由图8可以看出，绝热层厚度区间内，程序计算结果与图集值的差值Δδ≤9 mm，小于各区间的最大档次值10 mm。

通过以上对比可以看出程序计算结果与图集值偏差不大，可以在工程中用于计算不同情况下的绝热层厚度。

5 绝热层经济厚度影响因素分析

由式（1）、（2）、（4）可以看出，影响绝热层厚度的因素有D0、PE、T0、Ta、PT·S、W、t、λ。以下分别以硬质聚氨酯泡沫（a=0.024，b=0.000 14，PT=2 700元/m3）和岩棉板（a=0.036 4，b=0.000 18，PT=1 500元/m3）为绝热层材料来分析D0、PE、T0、t、λ对绝热层经济厚度的影响。

由图9可以看出，当管径由DN200增加到DN1000时，硬质聚氨酯绝热层厚度由41 mm增加到46 mm，增加5 mm，而岩棉绝热层厚度由62 mm增加到72 mm，增加10 mm，岩棉绝热层的增加厚度为聚氨酯的2倍。由以上分析可以得出，绝热层经济厚度随着管径的增大而增大；材料导热系数越大，绝热层经济厚度随管径的变化越大。

图9 管径对绝热层经济厚度的影响

由图10可以看出，当能量价格由35元/GJ增加到75元/GJ时，对于DN200的管道，硬质聚氨酯绝热层厚度由33 mm增加到47 mm，增加14 mm，而岩棉绝热层厚度由51 mm增加到71 mm，增加20 mm，岩棉绝热层的增加厚度为聚氨酯的1.4倍；对于DN1000的管道，硬质聚氨酯绝热层厚度由37 mm增加到53 mm，增加16 mm，而岩棉绝热层厚度由58 mm增加到84 mm，增加26 mm，岩棉绝热层的增加厚度为聚氨酯的1.6倍。由以上分析可以得出，绝热层经济厚度随着能量价格的提高而增大，且相同绝热材料下，大尺寸管道的增加量大于小尺寸管道，相同尺寸管道下，导热系数大的绝热材料增加量大于导热系数小的材料；相同的能量价格下，材料导热系数越大、管径越大，则其绝热层经济厚度大。

图10 能量价格对绝热层经济厚度的影响

由图11可以看出，当管道外表面温度由80 ℃增加到200 ℃时，对于DN200的管道，硬质聚氨酯绝热层厚度由35 mm增加到63 mm，增加28 mm，而岩棉绝热层厚度由53 mm增加到93 mm，增加40 mm，岩棉绝热层的增加厚度为聚氨酯的1.4倍；对于DN1000的管道，硬质聚氨酯绝热层厚度由39 mm增加到74mm，增加35mm，而岩棉绝热层厚度由62mm增加到115 mm，增加53 mm，岩棉绝热层的增加厚度为聚氨酯的1.5倍。由以上分析可以得出，绝热层经济厚度随着管道外表面温度的升高而增大，且相同绝热材料下，大尺寸管道的增加量大于小尺寸管道，相同尺寸管道下，导热系数大的绝热材料增加量大于导热系数小的材料；相同的管道外表面温度下，材料导热系数越大、管径越大，则其绝热层经济厚度越大。

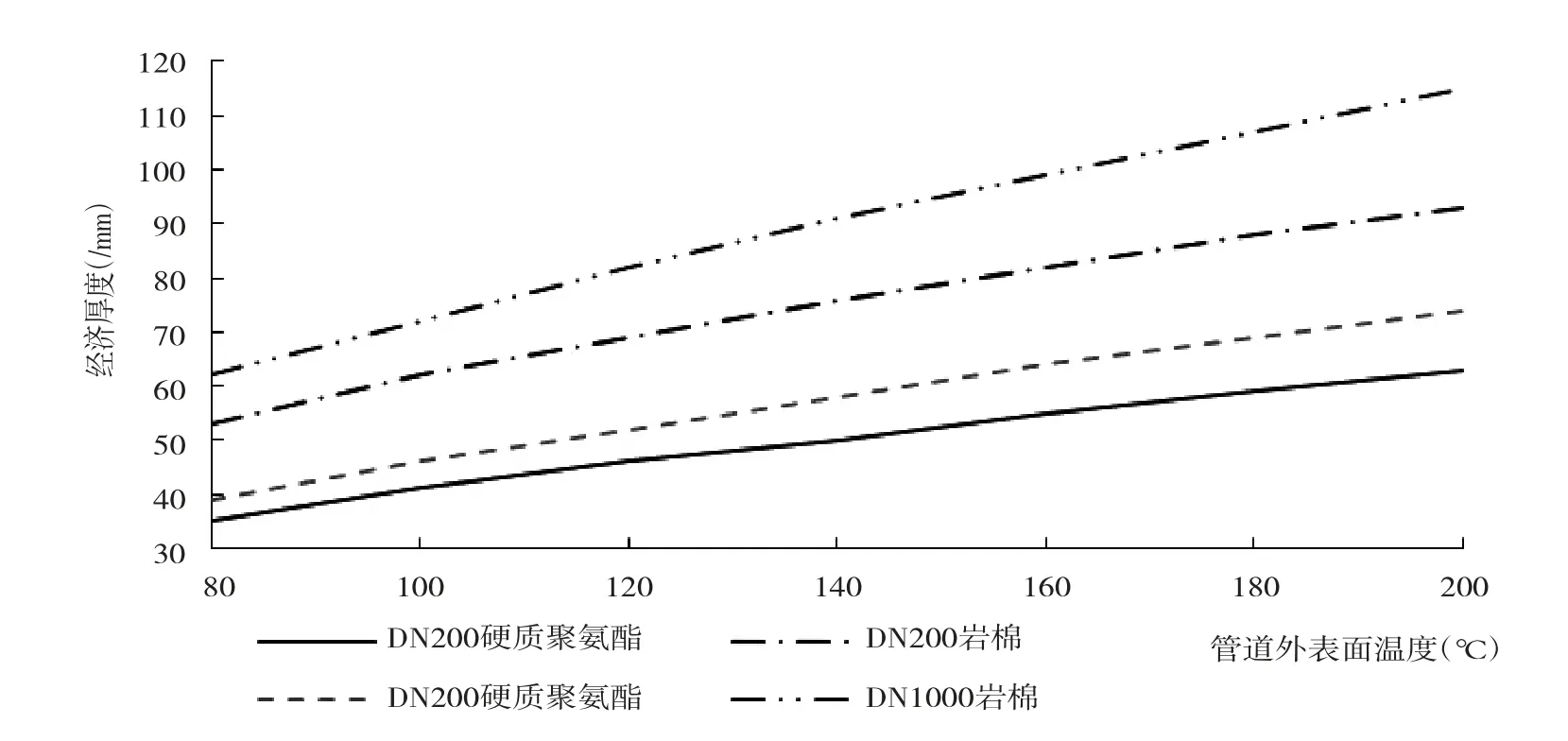
图11 管道外表面温度对绝热层经济厚度的影响

由图12可以看出：年运行时间越长，绝热层经济厚度越大。当年运行时间由1 000 h增加到4 000 h时，对于DN200的管道，硬质聚氨酯绝热层厚度由25 mm增加到47 mm，增加22 mm，而岩棉绝热层厚度由39 mm增加到72 mm，增加33 mm，岩棉绝热层的增加厚度为聚氨酯的1.5倍；对于DN1000的管道，硬质聚氨酯绝热层厚度由27 mm增加到54 mm，增加27 mm，而岩棉绝热层厚度由43 mm增加到85 mm，增加42 mm，岩棉绝热层的增加厚度为聚氨酯的1.6倍。由以上分析可以得出，绝热层经济厚度随着年运行时间的增加而增大，且相同绝热材料下，大尺寸管道的增加量大于小尺寸管道，相同尺寸管道下，导热系数大的绝热材料增加量大于导热系数小的材料；相同的年运行时间下，材料导热系数越大、管径越大，则其绝热层经济厚度越大。

图12 年运行时间对绝热层经济厚度的影响

由以上分析可总结出：绝热层经济厚度随管径、能量价格、管道外表面温度、年运行时间、导热系数的增大而增加，且相同绝热材料下，大尺寸管道的增加量大于小尺寸管道，相同尺寸管道下，导热系数大的绝热材料增加量大于导热系数小的材料。

6 结论与建议

（1）利用Dynamo计算管道绝热层经济厚度是可行的，为解决其他类似问题提供了一种思路。

（2）绝热层经济厚度随管径、能量价格、管道外表面温度、年运行时间、导热系数的增大而增加，且相同绝热材料下，大尺寸管道的增加量大于小尺寸管道，相同尺寸管道下，导热系数大的绝热材料增加量大于导热系数小的材料。

（3）导热系数小的材料，绝热层经济厚度随管径的变化小。当管径由DN200增加到DN1000时，岩棉绝热层的增加厚度为聚氨酯的2倍。

（4）当能量价格由35元/GJ增加到75元/GJ时，对于DN200的管道，岩棉绝热层的增加厚度为聚氨酯的1.4倍；对于DN1000的管道，岩棉绝热层的增加厚度为聚氨酯的1.6倍。

（5）当管道外表面温度由80 ℃增加到200 ℃时，对于DN200的管道，岩棉绝热层的增加厚度为聚氨酯的1.4倍；对于DN1000的管道，岩棉绝热层的增加厚度为聚氨酯的1.5倍。

（6）当管道年运行时间由1 000 h增加到4 000 h时，对于DN200的管道，岩棉绝热层的增加厚度为聚氨酯的1.5倍；对于DN1000的管道，岩棉绝热层的增加厚度为聚氨酯的1.6倍。