在问题解决中感悟数学模型

张树杉 王洪梅

[摘要]小学数学教材中渗透着很多的建模思想，通过对数量问题、总价问题、行程问题的教学片段进行分析比较，探讨如何加深学生对“归一问题”的理解，感悟数学思想、模型等，使建模思想得到有效渗透。

[关键词]问题解决;数学模型;归一问题

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020）20-0072-02

数学模型即“用数学的语言表达现实世界的故事”，是现实世界的简化及本质的描述。数学建模是指“从数学的角度对所需要研究的问题做一个模拟，去掉与之无关的因素，保留数学关系，以形成某种数学结构”。

《普通高中课程标准（2017）》指出：“数学建模是对现实问题进行数学抽象，用数学语言表达问题，用数学方法构建模型解决问题。”而小学阶段的数学建模与高中阶段的不同，模型的内容与建模的过程相对于高中的要求要低很多，但是小学数学教材中同样渗透着很多的建模思想。下面以三年级上册中的“归一问题”为例，谈谈如何在问题解决中让学生充分感悟数学模型。

【教学片段一】

出示例1：3件上衣用了15个扣子，15件上衣需要多少个扣子？

（教师在引导学生读懂题目意思的基础上，让学生独立思考、尝试解答，并鼓励学生用自己喜欢的方式解答）

生1：

师：能说一说你画的图表示什么含义吗？

生1：我先画了3件上衣，并标注了“15个”;第二排是15件上衣所需要的扣子的数量。

生2：

生3：

师：能说一说你这样画的理由吗？

生3：我用3段表示15个扣子，先求出一段需要多少个扣子，进而就可以求出15段（即15件上衣）需要多少个扣子。列式：15÷3=5（个），15x5=75（个）。

师：同学们画的图虽然简单，但能有效解决问题。从画图的情况看，我们首先需要知道一件衣服用了多少个扣子，然后才能求出15件衣服用了多少个扣子，即由“1”求“多”。

分析：数学中，把每一件上衣用了多少个扣子称为“每份数”，15件衣服即“份数”，15件衣服需要的扣子数称为“总数”，进而建立它们之间的关系“每份数×份数=总数”，建立数学模型，进而求解。

【教学片段二】

出示例2：7个书包140元，照这样，买10个书包需要用多少元？

师：能说一说你对题目的理解吗？

生4：我用1个圆圈表示1个书包，7个圆圈就表示7个书包，先求出1个书包的价钱，进而求出10个书包需要用多少钱。列式：140÷7=20（元），20x10=200（元）。

生5：我用7段表示7个书包的价钱，先求出一段也就是一个书包的价钱，进而求出10段也就是10个书包的价钱。列式：140÷7x10=200（元）。

师：你们的方法真好，太厉害了。

分析：数学中，把一个书包多少元称为“单价”，10个书包的“10”称为“数量”，10个书包的价格称为“总价”，进而建立它们之间的关系“单价×数量=总价”，从而顺利建模解答问题。

【教学片段三】

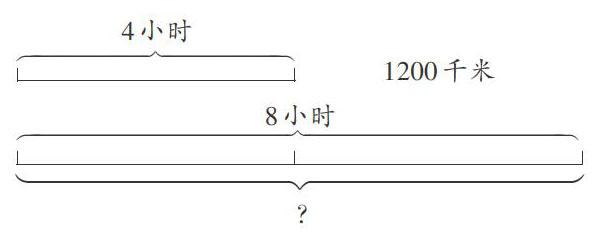
出示例3：4小时行驶了1200千米，8小时行驶多少千米？

师：这一题和前两题有点相似，说一说你是如何思考的。

生6：我用一条线段表示4小时行驶1200千米，要求8小时行驶多少千米，就可以用两条线段表示。列式：1200÷4=300（千米），300x8=2400（千米）。

生7：我和他想的不一样，我是这样想的，既然知道了4小时行驶了1200千米，要求8小时行驶多少千米，可以用8-4=4（小时），这样就多出了4个小时，所以8小时行驶了1200+1200=2400千米。

生8：我和他们想的都不一样。我是这样想的，4小时行驶了1200千米，而8刚好是4的2倍，所以8小时行驶了两个1200千米，即8÷4x1200=2400千米。

师：你真棒！知道和我们以前学习的“倍”的知识联系起来，真是个爱思考的学生。

分析：1小时行驶了多少千米，数学中称之为“速度”，8小时称为“时间”，8小时行驶的千米数称为“路程”。根据题意可建立相应的模型“速度×时间=路程”，进而求解。

【教学反思】

思考1：教学片段一利用的是“每份数×份数=总数”这一模型，教学片段二利用的是“单价×数量=总价”这一模型，教学片段三利用的是“速度×时间=路程”这一模型，这三类模型在数学中统称“归一问题”模型，即知道“1”可以求出“许多”，反之，知道“许多”也可以求出“1”。数学建模是一个极其复杂且具有挑战性的过程，也是一个“数学化”的过程，是让学生在某种学习中获得带有“模型”意义的数学结构的过程。小学数学没有复杂的数量关系与数学结构，其基本内容仍是以四则混合运算为主的问题解决。从成人的视角去看数学模型是及其简单的，但是学生独立思考、自主建构与解决问题的过程其实并不简单，许多问题的解决过程都是学生“再创造”的过程。

学生的数學学习能力与思维水平的提升离不开好的活动设计，尤其在小学阶段，数学建模思想的渗透与培养既要经历一个过程，也要兼顾不同水平和层次的学生的需求，这就要求教师要精心设计活动。上述的三个教学片段由相应的问题引出了丰富的学习材料。为了便于比较，促进学生的抽象概括能力，还对这些材料采用精准的呈现顺序，让学生经历了自主探究、独立思考、尝试解决的过程。在比较这些材料时，引导学生由“1”求出“许多”，使学生的感性认识上升为理性认识，既加深了学生对“归一问题”的理解，又突出了“归一问题”的结构特点与解题的规律。在整个建模的过程中，教师更加注重暴露学生学习的难点，逐步引导学生在质疑、争论、追问中逐步厘清问题。纵观整个学习过程，每一次的学习探究，学生都在体会题目的结构特点，都在感悟数学思想、数学模型等，建模思想得到了有效渗透。

思考2：人们认识客观世界，把握客观事物的规律，要通过探究事物与事物之间的异同，寻找事物与事物之间错综复杂的内在的联系来现实，这就需要对事物进行比较。通过比较，能够找出不同事物共同的本质属性，促进归纳概括和数学模型的建构。设计上述三道题的目的是想让学生能够主动地运用数学模型去比较、分析、解决一些同类的现实问题，深刻地感悟并理解数学模型思想。通过对“数量问题、总价问题、行程问题”进行分析比较，学生会发现“抛开情境，这些问题的本质与结构都是相同的”，进而窥探到数学模型的影子。不仅解决问题的过程能加深学生对数学模型的认识，建立数学模型的过程还能够帮助学生跳出具体的情境，向更高的抽象思维水平迈进。在数学教学中，教师既要教给学生“好吃又有营养”的数学内容（好吃是指学习的数学内容让学生感兴趣、热爱学;有营养是指教给学生数学的思想和方法），又要教会学生用数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界。

[参考文献]

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[s].北京：北京师范大学出版社，2012.

[2]史宁中.漫谈数学的基本思想[J].中国大学教学，2011（7）：9-11.

（责编 罗艳）