思维可视化在问题解决中的应用策略

徐娇

[摘要]通過实物图、图形图、线段图等图示充分暴露学生的思维过程，让学习可见;通过说图、对话、重构等，暴露学生的思维认知起点，重构学习概念;通过优化、掌握学习方法，暴露思维全过程，提升数学学习素养。

[关键词]小学数学;思维可视化;问题解决;策略

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020）20-0039-03

思维可视化是指把抽象的思考方法和过程通过可视的图式或图像呈现出来，让学生的思维充分暴露，让学习深度发生。

一、充分暴露学生的思维过程，让学习可见

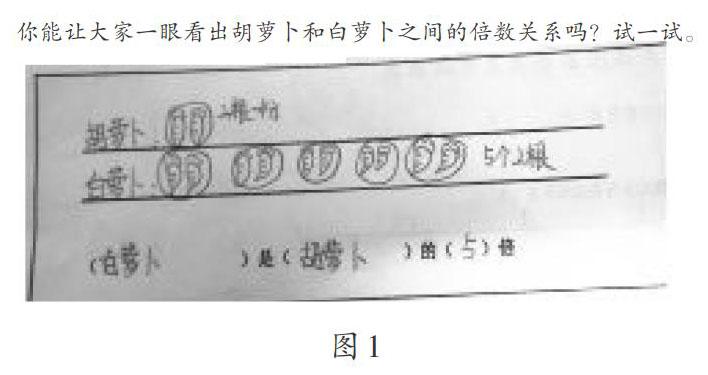
要暴露学生的思维过程，可以借助图示。画图是解决抽象问题时的常用手段，可以帮助学生直观理解题目的意图。如三年级上册第五单元“倍的认识”一课：

你能让大家一眼看出胡萝卜和白萝I、之间的倍数关系吗？试一试。

“倍的认识”是一个比较抽象的内容，学生比较难理解“倍”的意义、建立“倍”的概念。针对10根白萝卜和2根胡萝卜之间的倍数关系，让学生尝试画图，将思维可视化，真实了解学生的学习情况。

1.实物图

如图1所示，有的学生画出胡萝卜和白萝卜的实物图，然后通过圈一圈，直观地看出白萝卜的数量是胡萝卜的5倍。

2.图形图

如图2所示，有的学生把胡萝卜和白萝卜画成同一种图形，然后也是通过圈一圈，直观地看出白萝卜的数量是胡萝卜的5倍。这种方法更简洁明了，思维层次比画实物图高。

3.线段图

如图3所示，有的学生采用更抽象的数字和线段图来呈现自己的思维过程。他们将具体的萝卜数量抽象成数字，体现10里面有5个2，也就是10是2的5倍。

以上，教师引导学生借助多元表征将思维可视化，尊重不同个体的个性表达，关注了学生表征发展的层次，发展了学生的数学抽象、直观想象、逻辑推理、数学运算等学科核心素养。

二、暴露学生的思维认知起点，重构学习概念

1.说图，表达原始的思维过程

当学生把头脑中的思维通过画图的方式呈现后，还要用语言把画的图说出来，表达原始的思维过程。如“两位数乘两位数”的练习中有一道习题：

三年级跳集体舞的同学排成一个长方形。小婷站在左起第7列，右起第11列;从前数她是第8个，从后数她是第12个。你知道三年级共有多少人跳集体舞吗？

一位学生画图呈现了思维过程（如图4）。

（1）自己说，自己整理思路

“用1个圆圈代表1个人，小婷从左边数是第7个，从右边数是第11个，从前面数是第8个，从后面数是第12个，历以这样画。算式就是17x19。”这位学生用自己的语言描述，但是表述不完整。对于17x19这个算式，部分学生理解有困难。

（2）引导说，完善思维过程

在该生的基础上，笔者引导学生思考：“这个17代表什么？19又代表什么？为什么这两个数相乘，就是我们要求的答案？”学生继续思考，终于明白：“因为从左边数她是第7个，从右边数是第11个，她自己重复了，所以是7+11-1=17，说明一共有17列;从前面数她是第8个，从后面数是第12个，她自己也重复了，所以是8+12-1=19，即一列有19人。要求一共有多少人，就是17x19。”

学生通过画图表达自己的原始思考，再根据教师的引导完善自己的思维过程，充分把自己的思维过程体现出来并进行再思考，提升了思维的深刻性。

2.对话，审视思维过程的方法

课堂应该以学生为主体，教师要努力打造生本课堂。生生对话，能让学生用儿童化的语言表达个人的不同观点，审视自己的思维过程，实现思维的发展。在六年级上册第一单元“分数乘分数”中有一道练习题：李伯伯家有一块1/2公顷的地，种土豆的面积占了这块地的1/5，问：种土豆的面积是多少？

（1）生生对话，促进思考

对于图5、6两种不同的画法，让学生之间进行对话、提问，请作品主人说一说他是怎么想的。通过生生对话，图6的主人发现自己画的左图是表示1/2，右图是表示1/5，这两幅图的阴影部分的面积之和是1/2+1/5，而题目的意思明显不是用加法，求一个数的几分之几，应该用乘法解决。因此，图6明显画错了。在此过程中，课堂完全交给这些小主人，他们通过自行的交流、思考，自己就能把错误的做法给排除了。

（2）师生对话，引发思考

在交流过程中，学生认为图5的画法是正确的，它表示把长方形先平均分成2份，取其中的一份就是1/2，再把1/2平均分成5份，取其中的一份就是1/2的1/5，也就是1/10。当教师第一次询问是否都同意这样画，有没有什么不同的画法或建议时，学生都认为这样画已经很好了。教师再次提问：“那你们知道1/2在哪里吗？1/5又在哪里？”此刻，学生才意识到要把1/2也清楚地标注出来，然后在这个1/2里找它的1/5，让人一眼就看得清楚。经过交流、思考、修改，学生展示了最后的作品（如图7）。

当学生的学习无法继续的时候，教师要适时地引导，促使学生思考与反思，这样才能更进一步提升学生的数学思维能力。

3.重构，巩固已有的思维方式

“错误”是学生学习中的一种思维过程的体现，也是课堂教学中的宝贵教学资源，我们要充分暴露学生的思维，促进学生情感和思维的发展。如“数学广角——搭配（二）”的练习课中，部分学生对于这两种类型的题往往分不清。

类型1：王老师有3件上衣，2条裤子，一共有多少种搭配？

类型2：5个小朋友，每两个人通一次电话，一共需要通多少次电话？

对于衣服和裤子的搭配，学生列出的算式是3x2=6（种），用乘法;对于互通电话列出的算式是5x2=10（次），也是用乘法。

（1）与错误对话，重构已有的错误认知

教师先让学生把目光聚焦到类型2这道题，询问：“你是怎么想的？你能画一画吗？”学生呈现的图示如图8所示。从图示可以看出，学生把两种类型的题目搞混了，列出的算式与图示不符。通过让学生思考“1号和2号能通电话吗？1号和3号能通电话吗？”，让学生了解这样理解是不全面的，1号与2、3、4、5号都能通电话，而2号再和1号通电话就是重复了，所以这个类型的题目并不是用“搭配衣服”的模型来解决。通过与错误对话，重构学生的认知。

（2）与模糊对话，明晰已有的认知起点

从图8可以看出，学生对于两种类型的题目的认知是模糊的，脑海中没有清晰的思路和明确的认识。这就要求教师在学生思路模糊的时候，及时帮助他们明晰已有的认知起点，把两种类型重新建构。

图9解决的是类似每2人之间打电话、送信、比賽等问题，不能重复计算，对应类型2;而图10解决的是从两个类别中各选取一项进行搭配，对应类型1。这两个类型的题目其数学模型就是“组合”问题。学生在解决这两类问题时，要分清楚是哪种类型的问题，再通过画图等方式，选择合适的方法进行解答。

三、暴露思维过程的方法多样化，优化学习方法

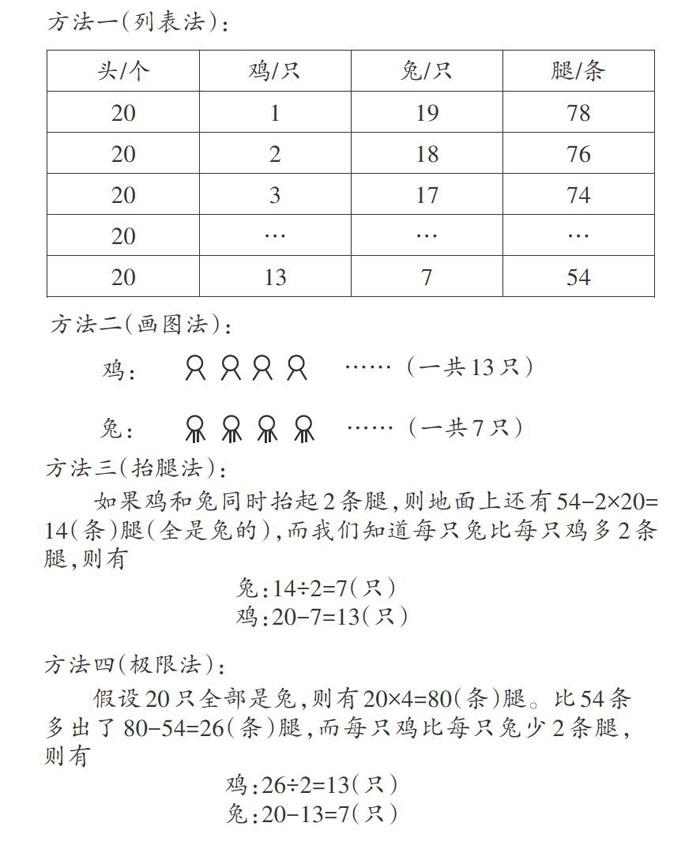
在暴露思维的过程中，学生的方法是多种多样的，都应给予肯定，但在学习多种方法后，还是要优化方法，寻找解题的最佳方案，提升数学学习的有效性。如“数学广角——鸡兔同笼”一课，学生对于鸡兔同笼问题的解法有很多。

例：鸡兔同笼，一共有20个头，54条腿，请问：鸡和兔各有多少只？

1.优化学习方法，暴露思维全过程

解决此问题主要有列表法、画图法、抬腿法、极限法（假设法）等。课上让学生进行各种方法的优化、比较，学生喜欢画图法和列表法的比较多，他们认为画图法和列表法能清晰、直观地知道鸡有几只、兔有几只;而抬腿法、极限法相较于画图法、列表法来说比较难理解。

2.掌握学习方法，提升数学学习素养

在解鸡兔同笼问题时，学生采用的画图法与教材中提供的方法一致;列表法则渗透着列举和猜想的思想方法;抬腿法和极限法渗透着假设的思想方法。由列举法和画图法的解题过程，可以归纳出解决此类问题的数学模型，因此也渗透了数学的模型思想。

思维可视化是一种解题的思路和策略，学生通过可视化的表达路径，在看图、说图、比较的过程中，掌握学习解决这类问题的方法，从而提高解决问题的能力，提升学科素养。

（责编吴美玲）