基于二阶锥规划的稳健低旁瓣自适应波束形成
刘 倩,朱安珏
(1.中国科学院声学研究所东海研究站,上海201815;2.中国科学院大学,北京100049)
0 引 言
在阵列信号处理中,旁瓣级大小一直是波束形成器设计中的一个重要指标。低旁瓣可以有效抑制来自旁瓣区域的干扰,降低目标检测的虚警概率。目前为止已经出现了大量有关波束旁瓣控制的算法。第一类为加窗法,例如Dolph-Chebyshev加权[1]可以在主瓣宽度一定的情况下获得最低的均匀旁瓣,但是该方法只适用于均匀线列阵,并且要求各阵元各向同性、不存在差异。第二类为基于自适应阵列理论的方法,例如Olen等在1990年提出的静态波束图数字综合方法[2]。该方法通过在旁瓣区域增加虚拟干扰源,运用自适应阵原理,采用迭代法调节干扰强度从而达到旁瓣控制的目的。该方法适用于任意阵型,并且不要求阵元满足各向同性,但在迭代过程中会引起波束主瓣的较快增宽并且迭代增益因子难以选择、迭代存在一定的收敛误差,导致波束旁瓣不能得到严格的控制。第三类为基于凸优化理论的波束图优化算法,例如Liu等[3]利用二阶锥规划(Second-Order Cone Programming, SOCP)方法设计的旁瓣控制自适应波束形成器,文献[4-5]提出了基于二阶锥规划的最低旁瓣波束形成器优化设计方法,该类方法适用于任意阵型并且对阵元无要求,可对波束旁瓣进行严格控制。
文献[1-3]中的旁瓣控制波束形成方法只将重点放在了旁瓣级控制方面,而对波束形成器的稳健性没有提出要求。文献[4-5]中,通过对加权向量的范数进行约束从而对波束形成器的稳健性进行提升,但在该方法中,加权向量范数的具体约束值通常是根据经验进行选取,不能通过计算得到严格的解。为了使该方法能运用于实际基阵,则需要更进一步提高旁瓣控制波束形成算法的稳健性。众所周知,自适应波束形成器的性能受到协方差矩阵与期望信号导向向量的影响,当期望信号存在于训练数据中,并且协方差矩阵估计不准时,自适应波束形成器的性能会出现很大程度的下降。针对以上情况,近年来已有多种改进算法对自适应波束形成器的稳健性进行讨论。其中一类是对期望信号导向向量进行估计,例如序列二次规划(Sequential Quadratic Programming, SQP)算法[6]、最少先验信息导向向量估计法[7]等。第二类是对协方差矩阵进行改进,其中较为经典的是原始对角加载算法(Load Sample Matrix Inversion, LSMI)[8]及其一系列改进算法,例如加权向量约束法(Norm Constrained Capon Beamforming, NCCB)[9]、最差性能最佳化(Worst-Case Performance Optimization, WCPO)[10]等。但是对角加载类算法在输入信噪比较高的情况下其输出信干噪比会出现较大程度的降低,其原因是,此类算法无法去除期望信号存在于训练数据中所带来的影响,接收信号中始终包含期望信号成分,当信噪比逐渐增高时,各类误差所导致的信号“自消”现象始终存在,导致自适应波束形成器产生较大的性能下降,而对角加载类方法无法改进这种性能下降。
本文针对自适应波束形成器的旁瓣控制和稳健性提高方面,提出了一种基于二阶锥规划的稳健低旁瓣自适应波束形成器设计方法,本方法对波束形成器的旁瓣级进行控制,并且利用干扰和噪声协方差矩阵重构法对波束形成器的稳健性进行提高,从而达到低旁瓣和高稳健性这两个目的。
1 基于SOCP的圆弧阵波束图设计
1.1 二阶锥规划简介
二阶锥规划是凸优化问题的一个子集,常常被用来解决波束优化设计问题。SeDuMi工具箱可专门用于解决二阶锥规划问题,其具有计算量小和计算结果精确的特点,并且可对优化问题的可解与否直接进行判别[11]。在SeDuMi中,标准的对称锥优化问题形式定义为
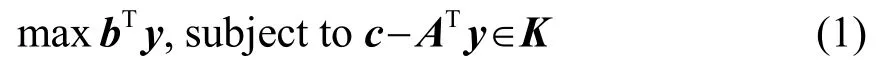
式中:y包含优化变量,A是任意矩阵,b与c是任意向量,K是一个对称锥集合,零锥与二阶锥都是对称锥的子集。
q维二阶锥的定义为
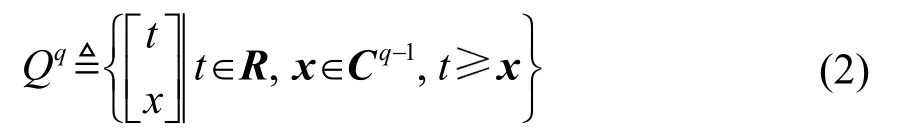
式中:x为所求优化变量,C为复数向量集,t为二阶锥的限定范围。
零锥定义为

式(3)可以代表等式约束。
波束优化设计问题即是将加权向量w的求解转化为在一系列线性等式与二阶锥约束条件下使得目标函数最大化的问题。即将约束问题写成如下形式:
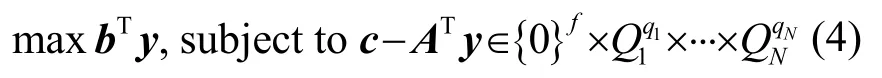
然后再利用已有的内点方法对上述问题进行求解。
1.2 干扰加噪声协方差矩阵重构
前面已经提到,对角加载类算法虽然可以对自适应波束形成的性能进行改进,但其输出信干噪比在输入信噪比较高时还是会出现较大程度的降低。因此,为了提高波束形成器的稳健性,一种有效的方法就是将协方差矩阵中的期望信号成分滤除。基于此思想,Gu等提出了干扰协方差矩阵重构算法[12]。该算法利用Capon空间谱估计,对期望信号存在区域以外的其他区域进行积分,从而获得重构的干扰加噪声协方差矩阵,减小了期望信号存在于接收信号中所带来的干扰。具体步骤如下:
假设观测区间由Θs与Θi+n两部分组成,其中Θs为期望信号所存在的区域,Θi+n为干扰信号存在的区域,sΘ与Θi+n互补。利用Capon空间谱估计作为空间谱分布,再对Θi+n区间进行积分则可得到重构的干扰加噪声协方差矩阵,即:
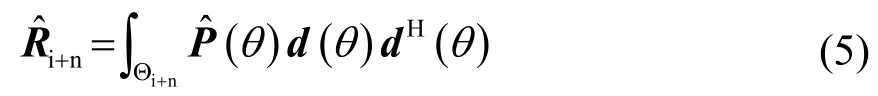
2 基于SOCP的稳健低旁瓣自适应波束形成
假设阵元数为N,波束的主轴方向为θs,旁瓣区域为ΘSL,θj∈ΘSL,则稳健低旁瓣自适应波束形成可以表述成下述问题:
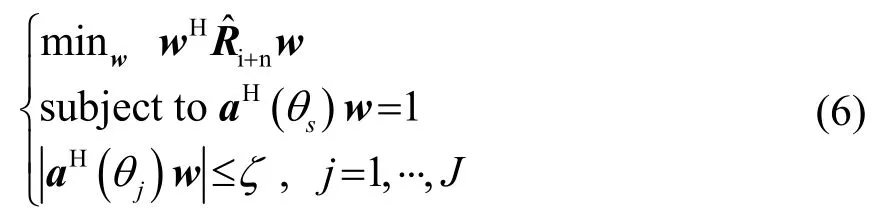
首先,利用楚列斯基(Cholesky)分解将上述问题中的二次目标函数转换为线性目标函数,即:

引入一个非负标量τ,使得Lw≤τ,则上述问题可以转化为
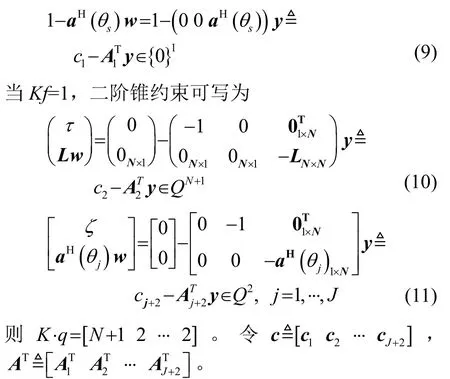
最后,将b、c、AT、K代入SeDuMi中即可求解出y和复加权向量w=[y3y4…yN]。
3 仿真分析
3.1 旁瓣控制性能分析
假设一半径为0.262 5 m、张角为165°的圆弧上均匀分布着384个阵元,定义圆心为极坐标原点,最中心两个阵元中垂线所在方向为0°方向。假设信号频率为390 kHz,选取相对0°方向对称的186个阵元在0°方向形成波束。在理想情况下,给出圆弧阵常规波束图和基于二阶锥规划的低旁瓣自适应波束图,如图1所示,放大后的波束图如图2所示。
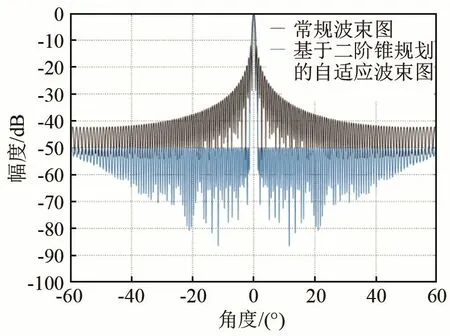
图1 理想情况下圆弧阵波束图Fig.1 Arc array beam pattern under ideal condition
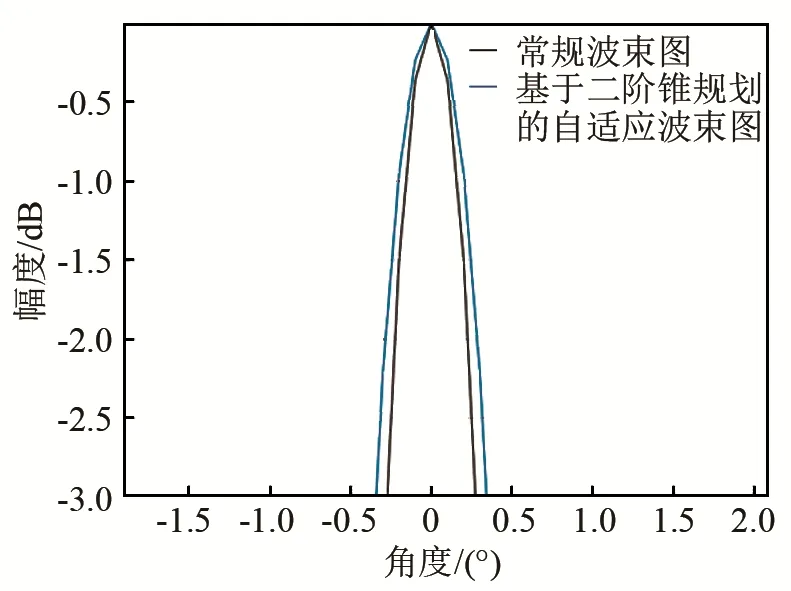
图2 放大后的波束图Fig.2 Enlarged beam pattern
由图1可以看出,圆弧阵的常规波束图旁瓣较高,最高旁瓣级大约为-11.95 dB,而基于二阶锥规划的低旁瓣自适应波束图可以将[-60°,-1.5°]∪[1.5°,60°]区域的旁瓣级控制到-50 dB。由图2可以看出,常规波束形成波束图-3 dB束宽约为0.55°,而基于二阶锥规划的低旁瓣自适应波束图-3 dB束宽增大到约0.86°。
3.2 稳健性分析
波束形成器的稳健性是指其在理想情况下获得的性能指标(如输出信干噪比)在存在各类失配情况下的下降程度。加权向量范数的大小是表征波束形成器稳健性高低的一个指标,波束加权向量范数越小,波束形成器对误差的灵敏度越低,稳健性越高。
本文将针对以下两种常见的失配情况,分别利用对角加载(LSMI)、最差性能最佳化(WCPO)以及协方差矩阵重构法(R-Reconstruction)对样本协方差矩阵进行改进,计算不同输入信噪比(Signal to Noise Ratio, SNR)情况下波束形成器的输出信干噪比(Signal to Interference plus Noise Ratio, SINR)以及加权向量范数的值,并与未进行改进的样本协方差矩阵求逆法(Sample Matrix Inversion, SMI)的输出信干噪比进行比较。
3.2.1 阵元位置与响应存在误差
在实际中,由于人工安装会导致阵元位置产生一定的误差,并且阵元会存在一定的方向性,导致方向幅度响应不同,从而给波束形成器的性能带来一定的影响。考虑阵元位置存在误差与阵元幅度响应具有一定的方向性的情况,假设上述圆弧阵各阵元真实位置所处角度与理想位置所处角度的误差服从[-0.05θ,0.05θ]的均匀分布,θ为阵元间隔角度,且各阵元具有方向性,-3 dB响应时的角度为90°。图3、4所示为阵元位置与幅度响应存在误差时的波束输出信干噪比及加权向量范数。
由图3、4可以看出,在存在阵元位置误差与响应误差的情况下,采用干扰协方差矩阵重构法(R-Reconstruction)对样本协方差矩阵进行改进后,相对于SMI、LSMI与WCPO方法,在输入信噪比逐渐增大的情况下,输出信干燥比略高于WCPO,远高于SMI与LSMI,并且具有最小的加权向量范数值,稳健性最高。
3.2.2 期望信号在传播过程中产生波前畸变
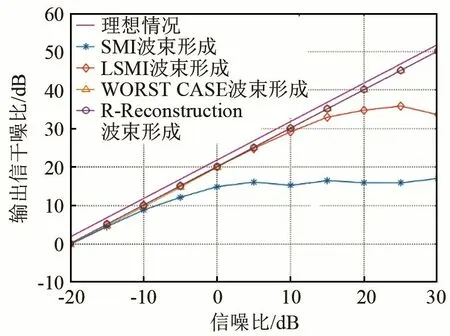
图3 阵元位置与幅度响应存在误差时的输出信干噪比Fig.3 Output SINR when error appears in sensor position and amplitude response
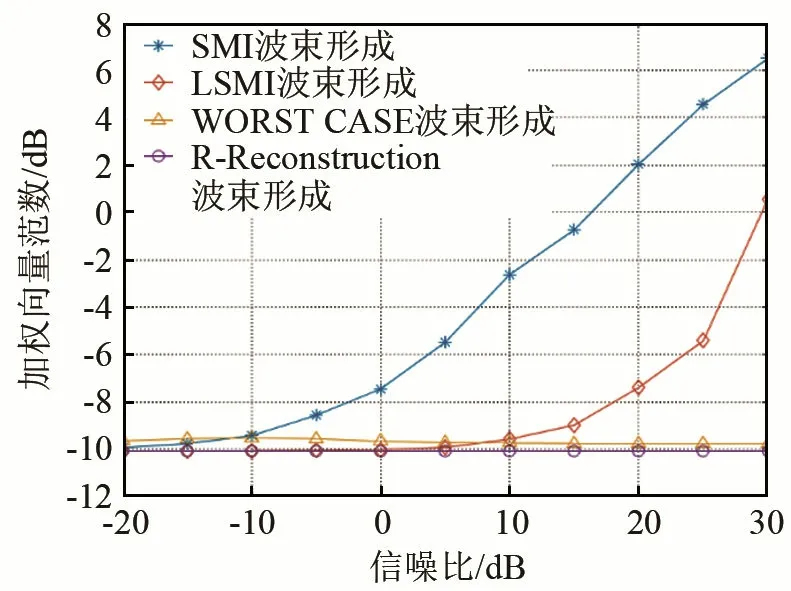
图4 阵元位置与幅度响应存在误差时的加权向量范数Fig.4 Norm of weight vector when error appears in sensor position and amplitude response
当期望信号在非各向同性介质中传播时,非常容易产生一定的幅度和相位的畸变,会导致期望信号导向向量产生一定的误差,从而波束形成器的性能下降。假设期望信号导向向量在传播过程中产生了相位畸变,相位误差服从均值为0、方差为0.04的高斯分布。图5、6所示为期望信号存在波前畸变时的波束输出信干噪比及加权向量范数。
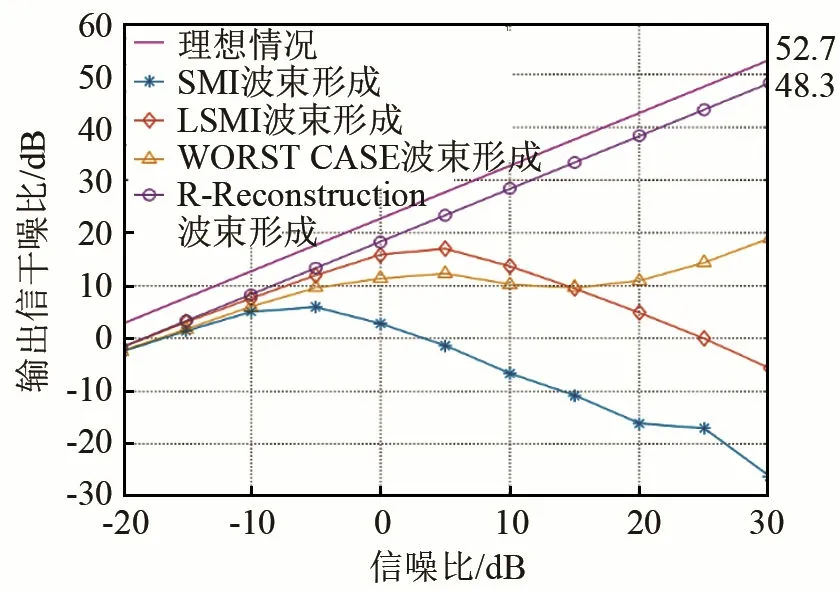
图5 期望信号存在波前畸变时的输出信干噪比Fig.5 Output SINR in the case of wavefront distortion
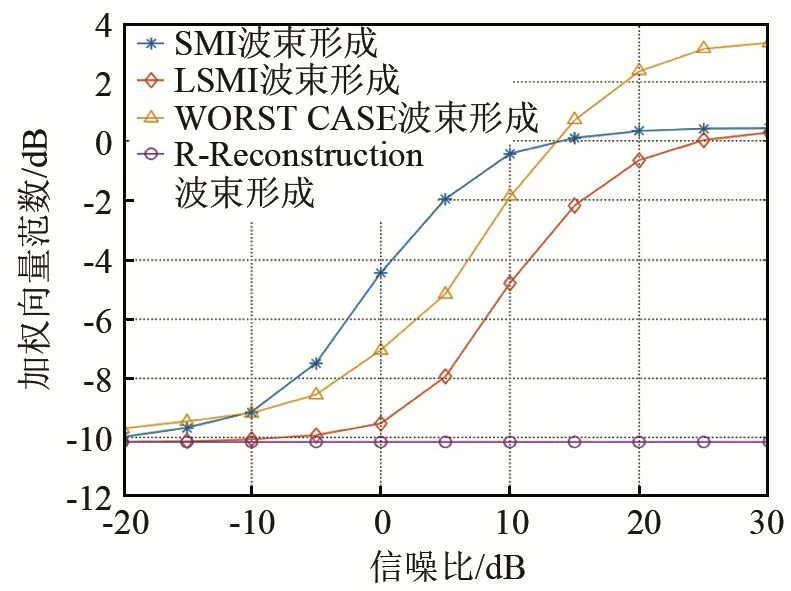
图6 期望信号存在波前畸变时的加权向量范数Fig.6 Norm of weight vector in the case of wavefront distortion
由图5、6可以看出,在期望信号存在波前畸变的情况下,在输入SNR 大于-10 dB之后,SMI、LSMI与WCPO算法的输出SINR均产生了很大程度的下降,而采用干扰协方差矩阵重构法(R-Reconstruction)对样本协方差矩阵进行改进后,相对于理想情况下的输出SINR只下降了约4 dB,性能下降远小于其他3种算法,并且其具有最小的加权向量范数值,稳健性最高。
综合上述两种失配情况下波束形成器的输出信干噪比和加权向量范数的结果可以看出,利用LSMI、WCPO和R-Reconstruction算法对样本协方差矩阵进行改进后,波束形成器的输出SINR相较于未进行改进的SMI算法均产生了较大程度的提高,但利用R-Reconstruction对样本协方差矩阵进行改进后,相较于利用LSMI与WCPO算法,输出SINR更高。并且当输入SNR增大时,输出SINR与理想情况下的输出SINR相差都为一定值,而其他方法在输入SNR逐渐增大的情况下,输出SINR下降程度越来越大,稳健性更低。
4 实验结果及分析
为了验证基于二阶锥规划的稳健低旁瓣自适应波束形成方法对成像效果的改进,进行了水池实验。首先将成像声呐放置在水池一侧的中间位置,在成像声呐中心线正前方6.78 m处放置一个点声源,与成像声呐同深度。成像声呐的基阵是具有384个阵元、半径为0.262 5 m、张角为165°的圆弧阵列,信号频率为390 kHz。实验中每186个阵元形成一个波束,共形成了384个波束。采用常规波束形成和基于二阶锥规划的稳健低旁瓣自适应波束形成的结果如图7所示。图7(a)为常规波束形成成像结果,7(b)为稳健低旁瓣自适应波束形成成像结果。图8为某距离处的输出强度。
从图7中可以看出,在无强干扰的情况下,利用上述两种方法均可以分辨出目标的位置。但是常规波束形成成像中目标的旁瓣级较高,在目标检测时易产生虚警。而本文提出的基于二阶锥规划的稳健低旁瓣自适应波束形成的成像,由于波束旁瓣级大大降低,因此目标变得更清晰,但是波束主瓣增宽,会在一定程度上降低成像声呐的分辨率。
从图8中可以看出,在对目标成像强度不变的情况下,本文所提算法可以将旁瓣区域的强度降低约10 dB左右,但并未达到仿真所得到的效果,产生此种情况的原因可能为:(1) 在仿真时对自适应波束形成失配情况考虑不全面;(2) 在协方差矩阵重构时,对于期望信号所存在的区域估计不准,导致在后续的优化计算中,旁瓣区域的设定存在问题,导致优化计算出的解存在误差。

图7 不同波束形成算法的成像效果Fig.7 The imaging effects of different beamforming methods
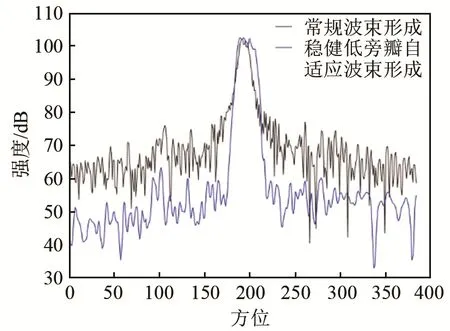
图8 某距离处的输出强度Fig.8 Output intensities at a distance
5 结 论
本文提出了一种基于二阶锥规划的稳健低旁瓣自适应波束形成算法,该算法利用二阶锥规划算法设计低旁瓣自适应波束形成,并且针对自适应波束形成容易受到各类失配因素的影响从而导致性能大幅下降的问题,利用干扰加噪声协方差矩阵重构法对该算法的稳健性进行提高。仿真结果表明,该算法在很大的输入信噪比范围内可以获得接近于理想情况下的输出信干噪比,并且加权向量范数最小,稳健性最高。水池实验结果证明,本文所提算法在成像时,可以在一定程度上降低旁瓣级,但是并未达到理论计算值,故本文所提算法还有待改进。

